2017 国庆湖南 Day5
期望得分:76+80+30=186
实际得分:72+10+0=82

先看第一问:
本题不是求方案数,所以我们不关心 选的数是什么以及的选的顺序
只关心选了某个数后,对当前gcd的影响
预处理
cnt[i] 表示 i的倍数有多少个
g[i][j] 表示gcd(i,第j张卡片上的数)
dp[i][j] 表示已经选了i个数,gcd=j 的 概率
再选k,要么gcd不变,要么变小
1、gcd不变
即k是j的倍数,因为已经选了i个且都是j的倍数,所以在剩下的n-i 个数中,还有 cnt[j]-i 个数可以选
所以状态转移方程:dp[i+1][j]+=dp[i][j]*(cnt[j]-i)/(n-i)
2、gcd变小
枚举要选的是第h个数 ,h满足gcd(a[h],j)!=j
(a[h] 表示第h张卡片上的数)
那么gcd会变为g[j][h]
因为 当gcd=1 的时候游戏结束,即 gcd=1 不能用来转移
所以 当gcd=1时,直接累计进答案,不更新dp
所以状态转移方程:dp[i+1][g[j][h]+=dp[i][j]/(n-i),g[j][h]!=1
答案的累计:
1、dp 过程中 gcd=1
只有 选了偶数个数之后,gcd=1,先手才赢
所以 在dp过程中,若i是奇数,ans+=dp[i][j]/(n-i)
(因为是在由i推出去的时候 累计答案,所以i是奇数)
2、dp完之后,没有牌选了
若n是奇数,则先手胜
所以若n是奇数,ans+=dp[n][i]
第二问:
就是裸地SG函数
sg[i][j] 表示 已经选了i个数,gcd=j 是必胜态(1)还是必败态(0)
根据
必胜态的后继状态至少有一个是必败态
必败态的后继状态全是必胜态
用 & 运算符可以方便的记录
记忆化搜索
边界:sg[n][i]=0,sg[i][1]=1
因为 选了n个数且j!=1 之后,对方败
当gcd=1 之后,对方胜
为什么要用对方的状态?(以下可能表述不清)
因为边界是在dfs 最前面判断的,而且是从选了0张牌开始
己方选了x张牌之后的状态,随dfs到了下一层里,即到了对方选的哪儿
如果己方选了n张牌且gcd!=1,己方赢,但sg[n][]的状态是到下一层dfs里判断的
主客交换,对方输,所以sg[n][]=0
sg[i][1] 同理

#include<cstdio> #include<cstring> #include<algorithm> #define N 301 #define K 1001 using namespace std; const double eps=1e-8; int n,m,a[N]; int cnt[K],g[K][N]; double dp[N][K]; int sg[N][K]; int getgcd(int a,int b) { return !b ? a : getgcd(b,a%b); } void init() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]),m=max(m,a[i]); } void pre() { for(int i=1;i<=n;i++) g[0][i]=a[i]; for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) cnt[i]+=(a[j]%i==0),g[i][j]=getgcd(i,a[j]); } void getprobability() { double ans=0.0; dp[0][0]=1.0; for(int i=0;i<n;i++) for(int j=0;j<=m;j++) if(dp[i][j]>eps) { dp[i+1][j]+=dp[i][j]*(cnt[j]-i)/(n-i); for(int k=1;k<=n;k++) if(g[j][k]!=j) { if(g[j][k]!=1) dp[i+1][g[j][k]]+=dp[i][j]/(n-i); else ans+=(i&1)*dp[i][j]/(n-i); } } if(n&1) for(int i=0;i<=m;i++) ans+=dp[n][i]; printf("%.9lf",ans); } int dfs(int x,int gcd) { if(sg[x][gcd]!=-1) return sg[x][gcd]; bool win=true; if(cnt[gcd]>x) win&=dfs(x+1,gcd); for(int i=1;i<=n;i++) if(g[gcd][i]!=gcd) win&=dfs(x+1,g[gcd][i]); return sg[x][gcd]=!win; } void getsg() { memset(sg,-1,sizeof(sg)); for(int i=0;i<=m;i++) sg[n][i]=0; for(int i=0;i<=n;i++) sg[i][1]=1; if(dfs(0,0)) printf("1.000000000"); else printf("0.000000000"); } int main() { freopen("cards.in","r",stdin); freopen("cards.out","w",stdout); init(); pre(); getprobability(); printf(" "); getsg(); }

80分暴力:
删边转化成倒着加边
每次 加一条边,两个端点重新做树形DP,得到合并之后的树的权值
用并查集维护连通块
一个连通块就是一棵树,答案就是所有 连通块的权值的乘积
维护乘积 乘一下再除一下就好了,考场上智商全掉了 用的线段树
100分做法:
上述做法慢就慢在每次加一条边,两个端点重新做树形DP
这里有一个结论:
设树S1最大权值路径的两端点为u1,u2
设树S2最大权值路径的两端点为v1,v2
那么树S1和树S2合并之后
最大权值路径的两端点一定是u1,u2,v1,v2中的两个
结论的简单证明:
设合并之后的最大权值路径的两端点为k1、k2
1、k1、k2 = u1、u2 或 k1、k2=v1、v2 ,显然成立
2、k1 = u1或u2,k2=v1或v2
如下图所示
若选的最长权值路径为路径P+路径L1
根据dfs求树的直径的原理可推得,
w——v1 和 w——v2 中必有一条是从w出发的最大权值路径
假设是w——v1
那么选路径P+路径L2 更优
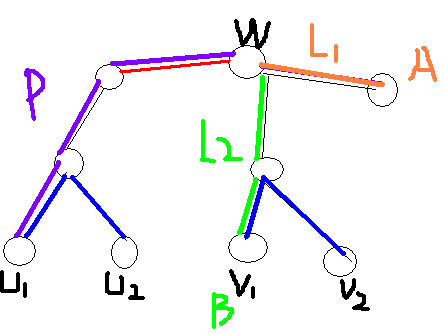
有了上述结论
那么我们每次合并只需要计算4条路径 、原来两棵树 的权值取最大
我么需要维护
val[i] 表示 当前i号连通块(树) 的最大权值
endpoint[i][2] 表示 i号连通块对应val[i] 的两端点
每次用最大的路径来更新这两个数组
每次的答案=原答案/val[S1]/val[S2]*合并之后的最大权值
如何计算路径权值?
dfs 一遍记录树上前缀和len[]
dis(u,v)=len[u]+len[v]-len[lca]+lca的权值

#include<cstdio> #include<iostream> #include<algorithm> using namespace std; #define N 100001 const int mod=1e9+7; int n,cnt; int cut[N],e[N][2]; int front[N],to[N<<1],nxt[N<<1],tot; int len[N],id[N]; int fa[N][18]; int a[N],val[N],ans[N]; int endpoint[N][2]; int F[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void add(int u,int v) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; } void init() { read(n); ans[n]=1; for(int i=1;i<=n;i++) { read(val[i]); ans[n]=1ll*ans[n]*val[i]%mod; endpoint[i][0]=endpoint[i][1]=i; F[i]=i; a[i]=val[i]; } int u,v; for(int i=1;i<n;i++) { read(u); read(v); add(u,v); e[i][0]=u; e[i][1]=v; } for(int i=1;i<n;i++) read(cut[i]); } void dfs(int x,int f) { fa[x][0]=f; len[x]=len[f]+a[x]; id[x]=++cnt; for(int i=front[x];i;i=nxt[i]) if(to[i]!=f) dfs(to[i],x); } void prelca() { for(int j=1;j<18;++j) for(int i=1;i<=n;i++) fa[i][j]=fa[fa[i][j-1]][j-1]; } int getlca(int u,int v) { if(id[u]<id[v]) swap(u,v); for(int i=17;i>=0;i--) if(id[fa[u][i]]>id[v]) u=fa[u][i]; return fa[u][0]; } int getlength(int u,int v) { int lca=getlca(u,v); return len[u]+len[v]-2*len[lca]+a[lca]; } int find(int i) { return F[i]==i ? i : F[i]=find(F[i]); } int Pow(int a,int b) { int res=1; for(;b;a=1ll*a*a%mod,b>>=1) if(b&1) res=1ll*res*a%mod; return res; } void solve() { int u,v; int product=ans[n],mx; int l,e1,e2; for(int i=n-1;i;i--) { u=e[cut[i]][0],v=e[cut[i]][1]; u=find(u); v=find(v); if(val[u]>val[v]) mx=val[u], e1=endpoint[u][0], e2=endpoint[u][1]; else mx=val[v], e1=endpoint[v][0], e2=endpoint[v][1]; for(int j=0;j<2;j++) for(int k=0;k<2;k++) { l=getlength(endpoint[u][j],endpoint[v][k]); if(l>mx) { mx=l; e1=endpoint[u][j]; e2=endpoint[v][k]; } } product=1ll*product*Pow(val[u],mod-2)%mod; product=1ll*product*Pow(val[v],mod-2)%mod; product=1ll*product*mx%mod; ans[i]=product; F[u]=F[v]; endpoint[v][0]=e1,endpoint[v][1]=e2; val[v]=mx; } for(int i=1;i<=n;i++) printf("%d\n",ans[i]); } int main() { freopen("forest.in","r",stdin); freopen("forest.out","w",stdout); init(); dfs(1,0); prelca(); solve(); }
80分暴力

#include<cstdio> #include<iostream> #include<algorithm> using namespace std; #define N 100001 #define lowbit(x) x&-x const int mod=1e9+7; int val[N],e[N][2],cut[N]; int front[N],to[N<<1],nxt[N<<1]; int tmp,tot,n; int f[N][2],out[N]; int F[N]; int st[4],ans1,ans2; int g[N<<2]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void add(int u,int v) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; } void build(int k,int l,int r) { g[k]=val[l]; if(l==r) return; int mid=l+r>>1; build(k<<1,l,mid); build(k<<1|1,mid+1,r); g[k]=1ll*g[k<<1]*g[k<<1|1]%mod; } void change(int k,int l,int r,int pos,int w) { if(l==r) { g[k]=w; return; } int mid=l+r>>1; if(pos<=mid) change(k<<1,l,mid,pos,w); else change(k<<1|1,mid+1,r,pos,w); g[k]=1; if(g[k<<1]!=-1) g[k]=1ll*g[k]*g[k<<1]%mod; if(g[k<<1|1]!=-1) g[k]=1ll*g[k]*g[k<<1|1]%mod; } void init() { read(n); int m1=0,m2=0; out[n]=1; for(int i=1;i<=n;i++) { read(val[i]); out[n]=1ll*out[n]*val[i]%mod; F[i]=i; if(val[i]>=m1) m2=m1,m1=val[i]; else if(val[i]>m2) m2=val[i]; } int u,v; for(int i=1;i<n;i++) read(e[i][0]),read(e[i][1]); for(int i=1;i<n;i++) read(cut[i]); build(1,1,n); } void dfs(int x,int fa) { bool leave=true; for(int i=front[x];i;i=nxt[i]) if(to[i]!=fa) { leave=false; dfs(to[i],x); if(f[to[i]][0]>=f[x][0]) f[x][1]=f[x][0],f[x][0]=f[to[i]][0]; else if(f[to[i]][0]>f[x][1]) f[x][1]=f[to[i]][0]; f[to[i]][0]=f[to[i]][1]=0; } f[x][0]+=val[x]; tmp=max(tmp,f[x][0]+f[x][1]); if(!leave) f[x][1]+=val[x]; } int find(int i) { return F[i]==i ? i : F[i]=find(F[i]); } void solve() { int res1,res2,res; int u,v; for(int i=n-1;i;i--) { u=e[cut[i]][0]; v=e[cut[i]][1]; res=0; tmp=0; dfs(u,0); res=max(res,tmp); res1=f[u][0]; f[u][0]=f[u][1]=0; tmp=0; dfs(v,0); res=max(res,tmp); res2=f[v][0]; f[v][0]=f[v][1]=0; change(1,1,n,find(v),-1); F[find(v)]=find(u); change(1,1,n,F[u],max(res,res1+res2)); out[i]=g[1]; add(u,v); } for(int i=1;i<=n;i++) printf("%d\n",out[i]); } int main() { freopen("forest.in","r",stdin); freopen("forest.out","w",stdout); init(); solve(); }

std:

# include<iostream> # include<cstdio> # include<cstring> # include<cstdlib> using namespace std; const int pp=1000000007; int c[2008][2008],f[2008],p[2008],ni[2008]; int n,m,k,nn; inline int power(int x,int n) { int ans=1,tmp=x; while (n) { if (n&1) ans=(long long)ans*tmp%pp; tmp=(long long)tmp*tmp%pp;n>>=1; } return ans; } void Count_c() { for (int i=0;i<=nn;i++) c[i][0]=1; for (int i=1;i<=nn;i++) for (int j=1;j<=i;j++) { c[i][j]=c[i-1][j-1]+c[i-1][j]; if (c[i][j]>=pp) c[i][j]-=pp; } } void Count_p() { int mm=(m-2)*n; for (int i=0;i<=nn;i++) p[i]=power(i,mm); } void Count_f() { f[0]=0;f[1]=1; for (int i=2;i<=nn;i++) { f[i]=power(i,n); for (int j=1;j<i;j++) { f[i]-=(long long)f[j]*c[i][j]%pp; if (f[i]<=-pp) f[i]+=pp; } if (f[i]<0) f[i]+=pp; } } void Count_ni() { ni[1]=1; for (int i=2;i<=nn;i++) ni[i]=power(i,pp-2); } int main() { freopen("photo.in","r",stdin); freopen("photo.out","w",stdout); scanf("%d%d%d",&n,&m,&k); nn=min(n,k); if (m==1) printf("%d\n",power(k,n)); else { Count_c(); Count_p(); Count_f(); Count_ni(); long long tmp=1,tmp1=1,sum=0,sum1; for (int s=1;s<=nn;s++) { tmp=tmp*ni[s]%pp; tmp=tmp*(k-s+1)%pp; tmp1=1;sum1=0; for (int j=0;j<=s;j++) { sum1+=tmp1*c[s][s-j]%pp*p[s-j]%pp; if (sum1>=pp) sum1-=pp; tmp1=tmp1*ni[j+1]%pp; if (k-s<j+1) break; tmp1=tmp1*(k-s-j)%pp; } sum+=tmp*f[s]%pp*f[s]%pp*sum1%pp; if (sum>=pp) sum-=pp; } printf("%d\n",sum); } fclose(stdin); fclose(stdout); return 0; }


