2017北京国庆刷题Day5 morning

期望得分：0+60+60=120

实际得分：0+30+60=90

 

令g=gcd（X11,X12,X13……）

则行列式可能为D的充要条件为g|D

1、g|D为必要条件：

     由定义来算行列式的时候，每一项都要从第一行里取一个数，所以g|D

2、g|D为充分条件：

    首先可以通过矩阵的初等变换，将矩阵X消成对角矩阵

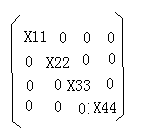
  其中，X11* X22 * X33* X44=D

  上述矩阵等价于

  

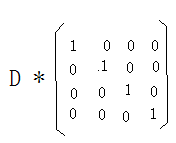
 把D拆为g*D/g

 还原到矩阵中

即

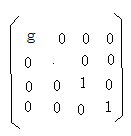      X22=

此矩阵模拟先前初等变换即可还原为原矩阵X

 

#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <cmath>

using namespace std;

int gcd(int a,int b) { return !b ? a : gcd(b,a%b); }

bool solve() 
{
    int n,m,x,y;  
    scanf("%d%d",&n,&m);
    x=0;
    for (int i=1;i<=n;++i) 
    {
        scanf("%d",&y);
        x=gcd(x,abs(y));
    }
    if (n==1) return y==m;
    if (!x) return !m;
    return !(abs(m)%x);
}

int main() 
{
    freopen("det.in","r",stdin);
    freopen("det.out","w",stdout);
    int t;
    scanf("%d", &t);
    while(t--)
        if (solve()) printf("Y\n");
        else printf("N\n");
}

 

 

 

每次分两半的时候，一定是奇数在左边，偶数在右边

所以用类似于线段树的思想来分治

由于每次讲将序列按奇偶下标分成两半，如果每次处理分成的那一半区间

那这个区间一定是一个等差数列,且公差为 2^d

所以

如果我们将区间离散化为1,2,3，……

那么完全可以求出区间离散化之后的答案，在回溯往上的时候每次*2（奇数*2-1），便可得到原区间的答案

 

例：1 2 3 4 5 6 7

第一次分治：

原左区间：     1 3 5 7     原右区间 2 4 6

离散化后区间  1 2 3 4                   1 2 3

离散化后左区间 总和 1+2+3+4=10

当回溯到上一层是，实际上是（1*2-1）+（2*2-1）+（3*2-1）+（4*2-1）= 10*2-4=16

离散化后右区间 总和 1+2+3=6

当回溯到上一层是，实际上是 （1*2）+（2*2）+（3*2）=6*2=12

 

具体怎么求？

设当前分治到 rr，l，r，x，y

表示当前区间离散化后为[1,2,……rr]，当前要求下标在本区间的[l,r]内，大小 在 本区间离散化后[x,y]之间

分四种情况：

1、对答案有贡献的数全在当前区间内，即 l=1 && r=rr

      因为每次分治的区间是一个等差数列，根据求和公式，本区间的答案为（y-x+1）*（x+y）/2

2、对答案有贡献的数是当前区间的一部分且全在左区间，即r<=mid ，那就递归到左区间求解

     在左区间中 ，rr变成mid，l，r 不变，x变为x/2+1，y变为（y+1）/2

3、对答案有贡献的数是当前区间的一部分且全在右区间，即l>mid，那就递归到右区间求解

    在右区间中，rr变成rr-mid，l-=mid，r-=mid，x变为（x+1）/2，y变为y/2+1

4、对答案有贡献的数是当前区间的一部分且左右区间都有，左右区间都递归，再合并

     这里 l，r  根上面的左右区间有所不同

     左区间的r是mid，右区间的l是1

 

上面提到了左区间是奇数，回溯的时候 和变为*2-元素个数

所以 回溯时，除了返回 和，还要返回元素个数

用pair即可

 

小细节：等差数列求和的时候，（y-x+1）*（x+y）/2 乘法运算可能会爆long long

所以 判断哪个是偶数，先进行除法运算

#include<cstdio>
#include<iostream>

#define mp(a,b) make_pair((a),(b))

using namespace std;

typedef long long LL;
typedef pair<LL,LL>pr;

LL mod;

void read(LL &x)
{
    x=0; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
}

pr solve(LL rr,LL l,LL r,LL x,LL y)
{
    if(x>rr || l>r) return mp(0,0);
    if(l==1 && r==rr)
    {
        y=min(y,rr);
        LL s;
        if (!((x+y)&1))s=(x+y>>1)%mod*((y-x+1)%mod)%mod;
        else s=((x+y)%mod)*((y-x+1>>1)%mod)%mod;
        return mp(s,(y-x+1)%mod);
    }
    LL mid=rr+1>>1;
    if(r<=mid) 
    {
        pr res=solve(mid,l,r,(x>>1)+1,y+1>>1);
        return mp(((res.first<<1)-res.second)%mod,res.second);
    }
    if(l>mid)
    {
        pr res=solve(rr-mid,l-mid,r-mid,x+1>>1,y>>1);
        return mp((res.first<<1)%mod,res.second);
    }
    pr res1=solve(mid,l,mid,(x>>1)+1,y+1>>1);
    pr res2=solve(rr-mid,1,r-mid,x+1>>1,y>>1);
    return mp(((res1.first<<1)-res1.second+(res2.first<<1))%mod,(res1.second+res2.second)%mod);
}

int main()
{
    freopen("seq.in","r",stdin);
    freopen("seq.out","w",stdout);
    LL n,m;
    read(n); read(m); read(mod);
    LL l,r,x,y;
    while(m--)
    {
        read(l); read(r); read(x); read(y);
        pr ans=solve(n,l,r,x,y);
        printf("%I64d\n",(ans.first+mod)%mod);
    }
}

 

考场 30分 莫队 ，然而枚举有60

#include<cmath>
#include<cstdio>
#include<iostream>
#include<algorithm>
#define N 100001
#define lowbit(x) x&(-x)
using namespace std;
typedef long long LL;
int a[N],n,m,mod;
int bl[N];
LL c[N],ans[N];
struct node
{
    int l,r,x,y,id;
}e[N];
void read(int &x)
{
    x=0; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
}
void dfs(int l,int r,int k)
{
    if(l==r) return;
    int m=l+r>>1,t=m;
    dfs(l,m,k<<1);
    for(int i=l;i<=m;i++) if(a[i]+k<=n) a[++t]=a[i]+k;
}
bool cmp(node p,node q)
{
    if(bl[p.l]!=bl[q.l]) return bl[p.l]<bl[q.l];
    return p.r<q.r;
}
void add(int x,int w)
{
    while(x<=n) { c[x]+=w; x+=lowbit(x); }
}
LL query(int x)
{
    LL sum=0;
    while(x) { sum+=c[x]; x-=lowbit(x); }
    return sum;
}
void update(int pos,bool ty)
{
    if(ty)  add(a[pos],a[pos]);
    else add(a[pos],-a[pos]);
}
int main()
{
    freopen("seq.in","r",stdin);
    freopen("seq.out","w",stdout);
    read(n); read(m); read(mod);
    a[1]=1; dfs(1,n,1);
    for(int i=1;i<=m;i++) 
    {
        read(e[i].l),read(e[i].r),read(e[i].x),read(e[i].y);
        if(e[i].x>n) e[i].x=n;
        if(e[i].y>n) e[i].y=n;
        e[i].id=i;
    }
    int siz=sqrt(n);
    for(int i=1;i<=n;i++) bl[i]=(i-1)/siz+1;
    sort(e+1,e+m+1,cmp);
    int L=1,R=0,l,r;
    for(int i=1;i<=m;i++)
    {
        l=e[i].l; r=e[i].r;
        while(L<l) update(L++,0);
        while(L>l) update(--L,1);
        while(R<r) update(++R,1);
        while(R>r) update(R--,0);
        if(e[i].x>1) ans[e[i].id]=query(e[i].y)-query(e[i].x-1);
        else ans[e[i].id]=query(e[i].y);
    }
    for(int i=1;i<=m;i++) printf("%I64d\n",ans[i]%mod);
}

 

 树形DP+倍增

回想倍增法求LCA的过程

从大到小枚举k，每次跳2^k步，只要不越界就跳，最后一定能跳到LCA

因为跳的都是2的幂次步，所以每跳一步就是二进制加了一个1

先预处理fa[i][k],表示点i向上跳2^k 步的祖先节点

设 f[i][j] 表示最后一步跳了2^j步，跳到了点i的答案之和

cnt[i][j] 表示最后一步跳了2^j步，跳到了点i的方案数

因为有了倍增求lCA原理的保证，所以只需要考虑跳2的幂次步

 

设siz[i]表示以i为根的子树的大小

rt[i]=j 表示 当前点属于  i的子树里，以j为根节点的子树

假设dfs回溯到x，转移分两种：

1、以x为链的一个端点

枚举x向上跳2^k次，则v=fa[x][j]

那么ans+=siz[v]-siz[rt[v]]  ——所有非rt[v]子树的点，与x的LCA都是v，都会有1的贡献

（类似于点分治中要去除同一子树内合法的点）

cnt[v][k]++   f[v][k]++

2、x作为倍增过程中的一个中途点

那么枚举最后一步跳了2^i 跳到了x

枚举x再往上跳2^j步,则v=fa[x][j]

那么ans+=（f[x][i]+cnt[x][i]）*（siz[v]-siz[rt[v]]）

f[x][i] 是原来的答案，在以v做LCA时，又会用 （siz[v]-siz[rt[v]]）次

cnt[x][i] 是 要再往上跳2^j步，又有一个1的贡献

cnt[v][j]+=cnt[x][i]   f[v][j]+=f[x][i]+cnt[x][i]

 

例：1--2--3--4 如果4到1的距离为3，二进制为11，对答案的贡献为2

回溯到4的时候，以4为端点会累积3--4   2--4

回溯到3的时候，以3为端点会累积2--3  1--3

回溯到2的时候，以2为端点会累积1--2，以2为中途点会累积1--2--3--4

（4跳2^1累积到2里，然后在枚举2为中途点时，最后一步跳了2^1到2,2再往上跳2^0）

 

为什么在枚举3作为中途点的时候，不枚举跳了2^0次方到了3

因为此时3不是中途点，我们是按跳2^k，k是降序跳的

 

个人总结：支持本题不重不漏的原理就是倍增求LCA的原理

或者是说任意数可以拆为2^k1+2^k2+2^k3…… ki 依次递减

 

个人AC代码 

#include<cstdio>
#define N 100001

using namespace std;

typedef long long LL;

LL ans;

int front[N],nxt[N<<1],to[N<<1],tot;
int fa[N][17],siz[N],rt[N];
int cnt[N][17],f[N][17];

void add(int u,int v)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot;
}

void dfs1(int x,int y)
{
    fa[x][0]=y; siz[x]=1;
    for(int i=1;i<=16;i++) fa[x][i]=fa[fa[x][i-1]][i-1];
    for(int i=front[x];i;i=nxt[i])
        if(to[i]!=y) dfs1(to[i],x),siz[x]+=siz[to[i]];
}

void dfs2(int x)
{
    for(int i=front[x];i;i=nxt[i])
        if(to[i]!=fa[x][0]) rt[x]=to[i],dfs2(to[i]);
    for(int i=0;i<=16;i++)
    {
        ans+=siz[fa[x][i]]-siz[rt[fa[x][i]]];
        cnt[fa[x][i]][i]++;
        f[fa[x][i]][i]++;
    }
    for(int i=1;i<=16;i++)
        for(int j=0;j<i;j++)
        {
            ans+=LL(cnt[x][i]+f[x][i])*LL(siz[fa[x][j]]-siz[rt[fa[x][j]]]);
            cnt[fa[x][j]][j]+=cnt[x][i];
            f[fa[x][j]][j]+=f[x][i]+cnt[x][i];
        }
}

int main()
{
    freopen("bitcount.in","r",stdin);
    freopen("bitcount.out","w",stdout);
    int n;
    scanf("%d",&n);
    int u,v;
    for(int i=1;i<n;i++)
    {
        scanf("%d%d",&u,&v);
        add(u,v);
    }
    dfs1(1,0);
    siz[0]=siz[1]; nxt[0]=1;
    dfs2(1);
    printf("%I64d",ans);
}

 

自己加了中间输出辅助理解的std

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>

#define st first
#define nd second
using namespace std;

struct edge {
    int x;
    int nxt;
};
typedef long long LL;

const int N = 1E5 + 10;
edge e[2 * N];
int lca[N][17], hd[N], fa[N], sons[N], nxt[N], cnt[N][17], f[N][17];
int n, m, x, y, l;
LL ans;

void link(int x, int y) {
    e[++l].x = y;
    e[l].nxt = hd[x];
    hd[x] = l;
}

void dfs_lca(int x) {
    lca[x][0] = fa[x];
    sons[x] = 1;
    for (int i = 1; i <= 16; ++i)
        lca[x][i] = lca[lca[x][i - 1]][i - 1];
    for (int p = hd[x]; p; p = e[p].nxt)
        if (e[p].x != fa[x]) {
            fa[e[p].x] = x;
            dfs_lca(e[p].x);
            sons[x] += sons[e[p].x];
        }
}

void dfs_ans(int x) {
    for (int p = hd[x]; p; p = e[p].nxt)
        if (e[p].x != fa[x]) nxt[x] = e[p].x, dfs_ans(e[p].x);
    for (int i = 0; i <= 16; ++i) {
        ans += sons[lca[x][i]] - sons[nxt[lca[x][i]]];
        if(sons[lca[x][i]] - sons[nxt[lca[x][i]]]) printf("%d : sons[%d]-sons[%d]=%d\n",x,lca[x][i],nxt[lca[x][i]],sons[lca[x][i]] - sons[nxt[lca[x][i]]]);
        cnt[lca[x][i]][i]++;
        f[lca[x][i]][i]++;
    }
    for (int i = 1; i <= 16; ++i)
        for (int j = 0; j <= i - 1; ++j) {
            ans += LL(cnt[x][i] + f[x][i]) * LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]);
            if(LL(cnt[x][i] + f[x][i]) * LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]))
            printf("%d : cnt[%d][%d]+f[%d][%d] * sons[%d]-sons[%d] = %I64d\n",x,x,i,x,i,lca[x][j],nxt[lca[x][j]],LL(cnt[x][i] + f[x][i]) * LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]));
            cnt[lca[x][j]][j] += cnt[x][i];
            f[lca[x][j]][j] += f[x][i] + cnt[x][i];
        }
}

int main() {
    //freopen("bitcount.in", "r", stdin);
    //freopen("bitcount.out", "w", stdout);
    scanf("%d", &n);
    for (int i = 1; i < n; ++i) {
        scanf("%d%d", &x, &y);
        link(x, y);
        link(y, x);
    }
    dfs_lca(1);
    sons[0] = sons[1];
    nxt[0] = 1;
    dfs_ans(1);
    printf("%I64d\n", ans);
}

 

考场60分暴力

#include<cstdio>
#include<algorithm>
#define N 2001
using namespace std;
int front[N],to[N<<1],nxt[N<<1],tot;
int val[N],deep[N],id[N];
int lca[N][N],f[N][12];
int n;
void add(int u,int v)
{
    to[++tot]=v; nxt[tot]=front[u]; front[u]=tot;
    to[++tot]=u; nxt[tot]=front[v]; front[v]=tot;
}
int cal(int x)
{
    int sum=0;
    while(x) sum+=(x&1),x>>=1;
    return sum;
}
void dfs(int x,int dep,int fa)
{
    id[x]=++tot; deep[x]=dep;
    f[x][0]=fa;
    for(int i=front[x];i;i=nxt[i])
        if(to[i]!=fa) dfs(to[i],dep+1,x);
}
int getlca(int x,int y)
{
    if(id[x]<id[y]) swap(x,y);
    for(int i=11;i>=0;i--)
        if(id[f[x][i]]>id[y]) x=f[x][i];
    return f[x][0];
}
void prelca()
{
    for(int j=1;j<=11;j++)
        for(int i=1;i<=n;i++)
            f[i][j]=f[f[i][j-1]][j-1];
    for(int i=1;i<n;i++)
        for(int j=i+1;j<=n;j++)
            lca[i][j]=getlca(i,j);    
}
void solve()
{
    int ans=0;
    for(int i=1;i<n;i++)
        for(int j=i+1;j<=n;j++)
            ans+=val[deep[i]-deep[lca[i][j]]]+val[deep[j]-deep[lca[i][j]]];
    printf("%d",ans);
}
int main()
{
    freopen("bitcount.in","r",stdin);
    freopen("bitcount.out","w",stdout); 
    scanf("%d",&n);
    int u,v;
    for(int i=1;i<n;i++)  {  scanf("%d%d",&u,&v); add(u,v); }
    for(int i=1;i<=n;i++) val[i]=cal(i);
    tot=0; dfs(1,0,0);
    prelca();
    solve();
}