2017北京国庆刷题Day3 morning
期望得分:100+60+0=160
实际得分:100+30+0=130

考场上用的哈希

#include<cstdio> #include<cstring> #include<algorithm> using namespace std; #define mod 1000003 #define mod2 100003 char s[10000001]; bool vis[mod],vis2[mod2]; int hash1,hash2; int gethash() { int len=strlen(s); sort(s,s+len); hash1=s[0]-'A'+1,hash2=hash1; for(int i=1;i<len;i++) { hash1=(hash1*26+(s[i]-'A')+1)%mod; hash2=(hash2*26+(s[i]-'A')+1)%mod2; } } int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); int n,ans=0; scanf("%d",&n); while(n--) { scanf("%s",s); gethash(); if(!vis[hash1] || !vis2[hash2]) vis[hash1]=true,vis2[hash2]=true,ans++; } printf("%d",ans); }
std直接sort,map 判重结构体

#include<cstdio> #include<cstdlib> #include<cstring> #include<map> using namespace std; struct node { int z[30]; node() { memset(z,0,sizeof(z)); } bool operator<(const node &a)const { for (int b=1;b<=26;b++) if (z[b]!=a.z[b]) return z[b]<a.z[b]; return false; } }now; map<node,bool> use; int ans,n; char s[120]; int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); scanf("%d",&n); for (int a=1;a<=n;a++) { scanf("%s",s+1); int l=strlen(s+1); memset(now.z,0,sizeof(now.z)); for (int a=1;a<=l;a++) now.z[s[a]-'A'+1]++; if (!use[now]) use[now]=true,ans++; } printf("%d\n",ans); return 0; }

设分成的每段长为Li,g=gcd(Li)
那么一共有n/g 个单位
设f[g]表示以g为周长,且三边gcd为1 的三角形的个数
设h[n/g]表示把n/g个单位 分配给任意多个三角形的个数
那么 ans=Σ f[g]*h[n/g] (g|n)
求f[g]:
设g=a+b+c,且a<=b<=c
对b和c的大小分两种情况讨论:
① b==c :
==> g=a+2b,那么b∈[ceil(g/3),floor((g-1)/2)]
所以f[g]=floor((g-1)/2)- ceil(g/3) +1
② b<c :
a,b,c 的每一种方案都可以看做由 a,b,c-1的每一种方案转移过来
但有一种除外:a+b=c,因为此时a,b,c-1 合法,a,b,c 不合法
当g为偶数时,a+b+a+b=g,g=2*(a+b),所以有floor(g/4)个
所以f[g]=f[g-1]+ (b&1)? 0 : -g/4
然后因为要求三边长互质,所以枚举g的每个因数k,f[g]-=f[k]
求h[i]:
把i个物品分成任意份的方案数=C(i-1,0)+C(i-1,1)+……+C(i-1,i-1)
= 2^(i-1)

#include<cmath> #include<cstdio> #include<algorithm> #define N 1000001 const int mod=1e9+7; using namespace std; int f[N],g[N]; int divisor[N],cnt; void ADD(int &a,int b) { a+=b; a>=mod ? a-=mod : 0; } int main() { freopen("b.in","r",stdin); freopen("b.out","w",stdout); int n; scanf("%d",&n); for(int a=3;a<=n;a++) { f[a]=f[a-1]; ADD(f[a],(a-1>>1)-ceil(a*1.0/3)+1); ADD(f[a],(a&1) ? 0 : -a/4); } for(int a=1;a*a<=n;++a) if(n%a==0) { divisor[++cnt]=a; if(a*a!=n) divisor[++cnt]=n/a; } sort(divisor+1,divisor+cnt+1); for(int i=1;i<=cnt;i++) for(int j=1;j<i;j++) if(divisor[i]%divisor[j]==0) ADD(f[divisor[i]],mod-f[divisor[j]]); g[0]=1; for(int i=1;i<=n;i++) g[i]=g[i-1],ADD(g[i],g[i-1]); int ans=0; for(int i=1;i<=cnt;i++) ADD(ans,1ll*f[divisor[i]]*g[n/divisor[i]-1]%mod); printf("%d",ans); }
考场上WW的组合数,得了30,挂了30

#include<cstdio> using namespace std; int n; int one[1001]; int C[1001][1001]; const int mod=1e9+7; bool check(int i,int j,int k) { if(!i || !j || !k) return false; if(!((i<=j)&&(j<=k))) return false; if(i+j<=k) return false; if(j-i>=k) return false; return true; } void pre() { for(int i=1;i<=n;i++) for(int j=1;j<=i;j++) for(int k=j;k<=i;k++) if(check(j,i-j-k,k)) one[i]++; for(int i=0;i<=n;i++) C[i][0]=1; for(int i=0;i<=n;i++) C[0][i]=1; for(int i=2;i<=n;i++) for(int j=1;j<=i;j++) C[i][j]+=C[i-1][j-1]+C[i-1][j],C[i][j]%=mod; int tot,ans=0; for(int i=3;i<=n;i++) if(n%i==0) { tot=n/i; tot--; if(!tot) { ans+=one[i]; continue;} for(int j=1;j<=tot;j++) ans=(ans+1ll*one[i]*C[tot][j-1]*j)%mod; } printf("%d",ans); } int main() { freopen("b.in","r",stdin); freopen("b.out","w",stdout); scanf("%d",&n); pre(); }

这题竟然是个容斥原理
解决本题的关键:行交换、列交换对答案不影响
将左视图按从下往上递减,正视图从左往右递减排列
那整张图的高度从左下到右上呈阶梯状递减
这样所有高度相同的呈现倒‘L’形,如下图所示蓝色部分
如果我们按高度递减的顺序依次计算每个倒‘L’形的方案数,那么这些倒‘L’形相对独立
答案就是所有倒‘L’形答案的乘积
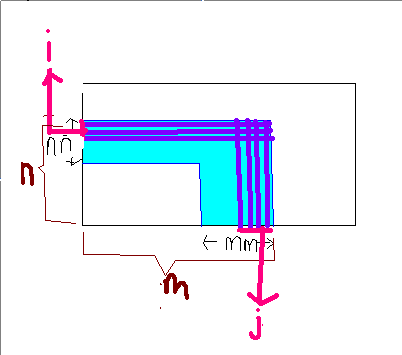
如何计算单个倒‘L’形的答案?——容斥原理
假设上图为已经按高度排好序的图
设当前正在处理高度为h的倒‘L’形
令nn表示当前有nn行的左视图高度为h,mm表示当前有mm列的主视图高度为h
n表示当前有n行的左视图高度>=h,m表示当前有m列的主视图高度>=h
定义性质pk表示 在这nn行mm列中,有k行/列不满足看到的高度为h
那根据容斥原理,
不具有任何一个性质p的方案和=
全集-Σ|pi|+Σ|pi∩pj|-Σ|pi∩pj∩pk|+…+(-1)^m*|p1∩p2∩…∩pm|
也就是所有方案-所有1行/列不满足条件的方案+所有2行/列不满足条件的方案-……
如何求有k行/列不满足条件的方案数?
设现在要求在倒‘L’形中,有i行j列不满足条件的方案数A,i+j=k
那么A分为两部分
① i行j列不能满足条件的部分:
当前高度为h,不能满足条件,每一个各自可以填[0,h-1],每个格子有h种方案
所以此时方案数=h^ (n*m-(n-i)*(m-j))
② 倒‘L’形中其他位置可以任意填的部分
当前高度为h,任意填就是可以填[0,h],每个各自有h+1种方案
所以此时的方案数=(h+1)^((n-i)*(m-j)-(n-nn)*(m-mm))
这是选定i行j列,所以还要乘上在nn行中选i行,在mm列中选j列的方案
终上所述,每个倒‘L’形 的答案为 (-1)^(i+j)* C(nn,i)* C(mm,j)* h^ (n*m-(n-i)*(m-j)) * (h+1)^((n-i)*(m-j)-(n-nn)*(m-mm))

#include<cstdio> #include<algorithm> using namespace std; typedef long long LL; #define N 51 #define H 10001 const int mod=1e9+9; int a[H],b[H]; int n,m; int C[N][N]; void pre(int k) { for(int i=0;i<=k;i++) C[i][0]=1; for(int i=1;i<=k;i++) for(int j=1;j<=i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; } int pow(int a,int b) { int res=1; for(;b;b>>=1,a=1ll*a*a%mod) if(b&1) res=1ll*res*a%mod; return res; } int cal(int n,int m,int nn,int mm,int h) { int res=0,tmp; for(int i=0;i<=nn;++i) for(int j=0;j<=mm;++j) { tmp=1ll*pow(h,n*m-(n-i)*(m-j))*pow(h+1,(n-i)*(m-j)-(n-nn)*(m-mm))%mod*C[nn][i]%mod*C[mm][j]%mod; if((i+j)&1) res=((res-tmp)%mod+mod)%mod; else res+=tmp,res%=mod; } return res; } int main() { freopen("c.in","r",stdin); freopen("c.out","w",stdout); int x; scanf("%d%d",&n,&m); for(int i=1;i<=n;++i) scanf("%d",&x),a[x]++; for(int i=1;i<=m;++i) scanf("%d",&x),b[x]++; pre(max(n,m)); LL res=1; int nown=0,nowm=0; for(int i=10000;i>=0;i--) if(a[i] || b[i]) { nown+=a[i]; nowm+=b[i]; res=1ll*res*cal(nown,nowm,a[i],b[i],i)%mod; } printf("%I64d",res); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号