「LibreOJ β Round #4」多项式 （广义欧拉数论定理）

https://loj.ac/problem/525

题目描述

给定一个正整数 kkk，你需要寻找一个系数均为 0 到 k−1之间的非零多项式 f(x)，满足对于任意整数 x 均有 $\mathrm{f(x)modk=0。你给出的多项式次数不能超过 60000，且最高次系数必须非 0。}$

输入格式

输入一行，包含一个正整数 k。

输出格式

若无解，则只输出一个整数 −1。否则首先输出一个整数 n 表示你寻找的多项式的次数，随后 n+1 个整数按照从低位到高位的顺序输出多项式的系数。

在此之后的输出将被忽略。

样例

样例输入

3

样例输出

4
0 1 2 2 1

即 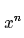 ≡ 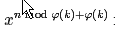mod k

即 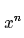 -  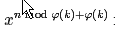≡ 0 mod k 

为了满足 n ≠ n mod φ(k) + φ(k) 且 n>=φ(k)

取n>=2*φ(k)

我取的n=2*φ(k)

那么 x^n - x^φ(k)  ≡ 0 mod k

因为题目要求系数都为非负整数

 x^n - x^φ(k)  ≡  x^n - x^φ(k) + k*x^φ(k) mod k

即 x^n - x^φ(k)  ≡  x^n  + （k-1）* x^φ(k)  mod k

所以多项式次数为n

n次方项系数为1，φ(k)次方项系数为k-1

 

注意k=1 时无解

#include<cmath>
#include<cstdio>
using namespace std;
int main()
{
    int k,kk;
    scanf("%d",&k);
    if(k==1) { printf("-1"); return 0; }
    kk=k;
    int phi=kk,m=sqrt(kk);
    for(int i=2;i<=m;i++)
        if(kk%i==0)
        {
            phi=phi/i*(i-1);
            while(kk%i==0) kk/=i;
        }
    if(kk>1) phi=phi/kk*(kk-1);
    int n=phi<<1;
    printf("%d\n",n);
    for(int i=0;i<n;i++) printf("%d ",i==phi ? k-1 : 0);
    printf("1"); 
}