洛谷 3373 【模板】线段树 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.将某区间每一个数乘上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

 

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2： 格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3： 格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

 

输出格式：

 

输出包含若干行整数，即为所有操作3的结果。

 

输入输出样例

输入样例#1：

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

输出样例#1：

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

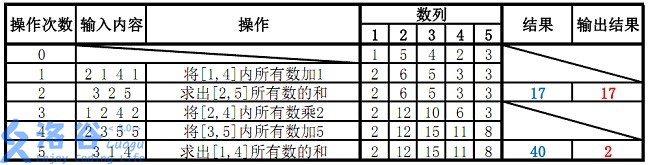
故输出应为17、2（40 mod 38=2）

 

先放乘再放加

放乘的时候加标记也乘

多开一个bool数组记录有没有乘标记，避免乘0不下传

#include<cstdio>
#define N 100001
using namespace std;
typedef long long LL;
int n,m;
int op,opl,opr;
LL sum[N<<2],fadd[N<<2],fmul[N<<2],w,p,ans;
bool mul[N<<2];
int mid[N<<2];
void build(int k,int l,int r)
{
    fmul[k]=1;
    if(l==r)
    {
        scanf("%d",&sum[k]);
        return;
    }
    mid[k]=l+r>>1;
    build(k<<1,l,mid[k]);
    build(k<<1|1,mid[k]+1,r);
    sum[k]=(sum[k<<1]+sum[k<<1|1])%p;
}
void down(int k,int l,int mid,int r)
{
    if(mul[k])
    {
        sum[k<<1]=sum[k<<1]*fmul[k]%p;
        sum[k<<1|1]=sum[k<<1|1]*fmul[k]%p;
        fadd[k<<1]=fadd[k<<1]*fmul[k]%p;
        fadd[k<<1|1]=fadd[k<<1|1]*fmul[k]%p;
        fmul[k<<1]=fmul[k<<1]*fmul[k]%p;
        fmul[k<<1|1]=fmul[k<<1|1]*fmul[k]%p;
        mul[k<<1]=mul[k<<1|1]=true;
        fmul[k]=1; mul[k]=false;
    }
    if(fadd[k])
    {
        sum[k<<1]=(sum[k<<1]+fadd[k]*(mid-l+1)%p)%p;
        sum[k<<1|1]=(sum[k<<1|1]+fadd[k]*(r-mid)%p)%p;
        fadd[k<<1]=(fadd[k<<1]+fadd[k])%p;
        fadd[k<<1|1]=(fadd[k<<1|1]+fadd[k])%p;
        fadd[k]=0;
    }
}
void solve(int k,int l,int r)
{
    if(l>=opl && r<=opr)
    {
        if(op==1)
        {
            sum[k]=sum[k]*w%p;
            fadd[k]=fadd[k]*w%p;
            fmul[k]=fmul[k]*w%p;
            mul[k]=true;
        }
        else if(op==2)
        {
            sum[k]=(sum[k]+w*(r-l+1)%p)%p;
            fadd[k]+=w;
        }
        else ans=(ans+sum[k])%p;
        return;
    }
    if(mul[k] || fadd[k]) down(k,l,mid[k],r);
    if(opl<=mid[k]) solve(k<<1,l,mid[k]);
    if(opr>mid[k]) solve(k<<1|1,mid[k]+1,r);
    sum[k]=(sum[k<<1]+sum[k<<1|1])%p;
}
int main()
{    
    scanf("%d%d%d",&n,&m,&p);
    build(1,1,n);
    while(m--)
    {
        scanf("%d",&op);
        if(op==1 || op==2)
        {
            scanf("%d%d%d",&opl,&opr,&w);
            solve(1,1,n);
        }
        else
        {
            ans=0;
            scanf("%d%d",&opl,&opr);
            solve(1,1,n);
            printf("%lld\n",ans);
        }
    }
}