卢卡斯定理

参考博客：

http://www.cnblogs.com/owenyu/p/6724560.html

http://blog.csdn.net/raalghul/article/details/51752369

http://www.cnblogs.com/candy99/p/6637629.html 

 

结论：

若p是质数，令n=a*p+b，m=c*p+d，  b，d ∈[0,p)

则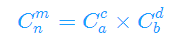

 

 

证明：

 

首先证明 在模p意义下

  

 

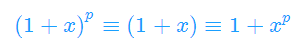
证明法一：

由费马小定理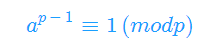， 得

 

 

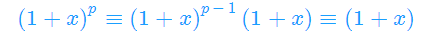
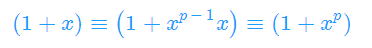
证明法二：

当j∈[1,p-1] 时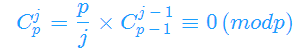， （p是质数，j∈[1,p-1]，j在模p意义下一定有逆元）

用二项式定理展开（1+x）^p

 

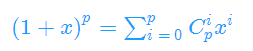
除了第一项和最后一项，中间项的组合数在模p意义下是0

所以

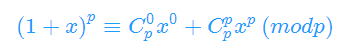
 这张图是盗来的http://www.cnblogs.com/owenyu/p/6724560.html

 

 

 

#include<cstdio>
using namespace std;
typedef long long LL;
LL f[100001];
void pre(int p)
{
    f[0]=1;
    for(int i=1;i<=p;i++) f[i]=f[i-1]*i%p;
}
int pow(LL a,int b,int p)
{
    LL r=1;
    while(b)
    {
        if(b&1) r*=a,r%=p;
        b>>=1; a*=a; a%=p; 
    }
    return r;
}
int C(int n,int m,int p)
{
    if(m>n) return 0; //如果m>n，那么原来的m<n-p,即m与n之间至少有一个p的倍数，那么结果为0 
    return f[n]*pow(f[m]*f[n-m],p-2,p)%p;
}
/*int Lucas(int n,int m,int p)
{
    if(!m) return 1;
    return (C(n%p,m%p,p)*Lucas(n/p,m/p,p))%p;
}*/
int Lucas(int n,int m,int p) //非递归版，上面是递归版 
{
    LL ans=1;
    for(;m;n/=p,m/=p) ans=ans*C(n%p,m%p,p)%p; 
    return ans;
}
int main()
{
    int T,n,m,p;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d",&n,&m,&p);
        pre(p);
        printf("%d\n",Lucas(n+m,m,p));
    }    
}