uva 11178 Morley's Theorem

https://vjudge.net/problem/UVA-11178

 

题意：三角形ABC的三等分线相交成等边三角形DEF

给出ABC坐标，输出DEF坐标

 

 

 

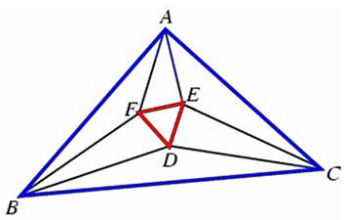
直线旋转求交点

#include<cmath>
#include<cstdio>

using namespace std;

struct Point
{
    double x,y;
    Point (double x=0,double y=0):x(x),y(y) { }    
    void output()
    {
        printf("%lf %lf ",x,y);
    }
};

typedef Point Vector;

Vector operator + (Vector A,Vector B) { return Vector(A.x+B.x,A.y+B.y); }
Vector operator - (Vector A,Vector B) { return Vector(A.x-B.x,A.y-B.y); }
Vector operator * (Vector A,double p) { return Vector(A.x*p,A.y*p); }
Vector operator / (Vector A,double p) { return Vector(A.x/p,A.y/p); }

struct Geometry
{
    double Dot(Vector A,Vector B)
    {
        return A.x*B.x+A.y*B.y;
    }
    double Length(Vector A)
    {
        return sqrt(Dot(A,A));
    }
    double Angle(Vector A,Vector B) 
    {
        return acos(Dot(A,B)/Length(A)/Length(B)); 
    }
    Vector Rotate(Vector A,double rad)
    {
        return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
    }
    double Cross(Vector A,Vector B)
    {
        return A.x*B.y-A.y*B.x;
    }
    Point GetLineIntersection(Point P,Vector v,Point Q,Vector w)
    {
        Vector u=P-Q;
        double t=Cross(w,u)/Cross(v,w);
        return P+v*t;
    }
};

Geometry Two_dimensional;

int main()
{
    int t;
    scanf("%d",&t);
    Point A,B,C,D,E,F;
    double a,b,c;
    Point T1,T2;
    while(t--)
    {
        scanf("%lf%lf",&A.x,&A.y);
        scanf("%lf%lf",&B.x,&B.y);
        scanf("%lf%lf",&C.x,&C.y);
        a=Two_dimensional.Angle(B-A,C-A);
        b=Two_dimensional.Angle(A-B,C-B);
        c=Two_dimensional.Angle(A-C,B-C);
        T1=Two_dimensional.Rotate(C-B,b/3);
        T2=Two_dimensional.Rotate(B-C,-c/3);
        D=Two_dimensional.GetLineIntersection(B,T1,C,T2);
        T1=Two_dimensional.Rotate(A-C,c/3);
        T2=Two_dimensional.Rotate(C-A,-a/3);
        E=Two_dimensional.GetLineIntersection(C,T1,A,T2);
        T1=Two_dimensional.Rotate(B-A,a/3);
        T2=Two_dimensional.Rotate(A-B,-b/3);
        F=Two_dimensional.GetLineIntersection(A,T1,B,T2);
        D.output(); E.output(); F.output();
        puts("");
    }
}