hdu 4940 Destroy Transportation system (无源汇上下界可行流)
Destroy Transportation system
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
http://acm.hdu.edu.cn/showproblem.php?pid=4940
Problem Description
Tom is a commander, his task is destroying his enemy’s
transportation system.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
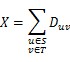
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
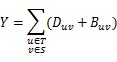
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
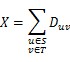
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
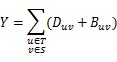
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Input
There are multiply test cases.
The first line contains an integer T(T<=200), indicates the number of cases.
For each test case, the first line has two numbers n and m.
Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)
The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.
The first line contains an integer T(T<=200), indicates the number of cases.
For each test case, the first line has two numbers n and m.
Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)
The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.
Output
For each case, output "Case #X: " first, X is the case
number starting from 1.If such set doesn’t exist, print “happy”, else print
“unhappy”.
Sample Input
2
3 3
1 2 2 2
2 3 2 2
3 1 2 2
3 3
1 2 10 2
2 3 2 2
3 1 2 2
Sample Output
Case #1: happy
Case #2: unhappy
Hint
In first sample, for any set S, X=2, Y=4. In second sample. S= {1}, T= {2, 3}, X=10, Y=4.题意:给出一个有向强连通图,每条边有两个值:破坏该边的代价a 和 把该边建成无向边的代价b
问是否存在一个集合S和S的补集T,满足 S到T的割边的 a的总和 > T到S的 割边的 a+b的总和
若存在 输出unhappy, 不存在,输出happy
以a为下界,a+b为上界,判断是否存在无源汇上下界可行流
因为如果存在,流量总和>=下界,<=上界
#include<cstdio> #include<cstring> #include<queue> #include<algorithm> #define N 210 #define M 15000 using namespace std; int m,n,src,dec,sum,tot; int a[N]; int front[N],to[M],nextt[M],cap[M]; int lev[N],cur[N]; queue<int>q; void add(int u,int v,int w) { to[++tot]=v; nextt[tot]=front[u]; front[u]=tot; cap[tot]=w; to[++tot]=u; nextt[tot]=front[v]; front[v]=tot; cap[tot]=0; } bool bfs() { for(int i=src;i<=dec;i++) cur[i]=front[i],lev[i]=-1; while(!q.empty()) q.pop(); lev[src]=0; q.push(src); int now; while(!q.empty()) { now=q.front(); q.pop(); for(int i=front[now];i;i=nextt[i]) if(cap[i]>0&&lev[to[i]]==-1) { lev[to[i]]=lev[now]+1; if(to[i]==dec) return true; q.push(to[i]); } } return false; } int dfs(int now,int flow) { if(now==dec) return flow; int rest=0,delta; for(int & i=cur[now];i;i=nextt[i]) if(cap[i]>0&&lev[to[i]]>lev[now]) { delta=dfs(to[i],min(flow-rest,cap[i])); if(delta) { cap[i]-=delta; cap[i^1]+=delta; rest+=delta; if(rest==flow) break; } } if(rest!=flow) lev[now]=-1; return rest; } int dinic() { int tmp=0; while(bfs()) tmp+=dfs(src,2e9); return tmp; } int main() { int T; scanf("%d",&T); for(int k=1;k<=T;k++) { memset(a,0,sizeof(a)); memset(front,0,sizeof(front)); sum=0; tot=1; scanf("%d%d",&n,&m); src=0; dec=n+1; int u,v,c,d; for(int i=1;i<=m;i++) { scanf("%d%d%d%d",&u,&v,&c,&d); a[v]+=c; a[u]-=c; add(u,v,d); } for(int i=1;i<=n;i++) if(a[i]<0) add(i,dec,-a[i]); else if(a[i]>0) {add(src,i,a[i]); sum+=a[i];} if(dinic()==sum) printf("Case #%d: happy\n",k); else printf("Case #%d: unhappy\n",k); } }


