NOIP2013 提高组 Day2
期望得分:100+100+30+=230+
实际得分:100+70+30=200
T2 觉得题目描述有歧义:
若存在2i却不存在2i+1,自己按不合法做的,实际是合法的
T3 bfs 难以估分
虽然得了30,但代码有bug,debug后50
https://www.luogu.org/problem/lists?name=&orderitem=pid&tag=83%7C30
T1 积木大赛
题目描述
春春幼儿园举办了一年一度的“积木大赛”。今年比赛的内容是搭建一座宽度为n的大厦,大厦可以看成由n块宽度为1的积木组成,第i块积木的最终高度需要是hi。
在搭建开始之前,没有任何积木(可以看成n块高度为 0 的积木)。接下来每次操作,小朋友们可以选择一段连续区间[l, r],然后将第第 L 块到第 R 块之间(含第 L 块和第 R 块)所有积木的高度分别增加1。
小 M 是个聪明的小朋友,她很快想出了建造大厦的最佳策略,使得建造所需的操作次数最少。但她不是一个勤于动手的孩子,所以想请你帮忙实现这个策略,并求出最少的操作次数。
输入输出格式
输入格式:
输入文件为 block.in
输入包含两行,第一行包含一个整数n,表示大厦的宽度。
第二行包含n个整数,第i个整数为hi 。
输出格式:
输出文件为 block.out
仅一行,即建造所需的最少操作数。
输入输出样例
5 2 3 4 1 2
5
说明
【样例解释】
其中一种可行的最佳方案,依次选择
[1,5] [1,3] [2,3] [3,3] [5,5]
【数据范围】
对于 30%的数据,有1 ≤ n ≤ 10;
对于 70%的数据,有1 ≤ n ≤ 1000;
对于 100%的数据,有1 ≤ n ≤ 100000,0 ≤ hi≤ 10000。
将积木的高度用点、线画出来
对于每一段上凸的部分,所需操作次数是它的最大值 - 前一段上凸部分的最右端

#include<cstdio> #define N 100011 using namespace std; int n,a[N]; struct node { int high,end; }e[N]; int cnt,ans; bool up; int main() { /*freopen("BlockNOIP2013.in","r",stdin); freopen("BlockNOIP2013.out","w",stdout);*/ scanf("%d",&n); for(int i=1;i<=n+1;i++) { if(i<=n) scanf("%d",&a[i]); if(!up&&a[i]>a[i-1]) { e[cnt].end=a[i-1]; up=true; cnt++; } else if(up&&a[i]<a[i-1]) { e[cnt].high=a[i-1]; up=false; } } ans=e[1].high; for(int i=2;i<=cnt;i++) ans+=e[i].high-e[i-1].end; printf("%d",ans); }
T2 花匠
题目描述
花匠栋栋种了一排花,每株花都有自己的高度。花儿越长越大,也越来越挤。栋栋决定
把这排中的一部分花移走,将剩下的留在原地,使得剩下的花能有空间长大,同时,栋栋希
望剩下的花排列得比较别致。
具体而言,栋栋的花的高度可以看成一列整数h1,h2..hn。设当一部分花被移走后,剩下的花的高度依次为g1,g2..gn,则栋栋希望下面两个条件中至少有一个满足:
条件 A:对于所有g(2i)>g(2i-1),g(2i)>g(2i+1)
条件 B:对于所有g(2i)<g(2i-1),g(2i)<g(2i+1)
注意上面两个条件在m = 1时同时满足,当m > 1时最多有一个能满足。
请问,栋栋最多能将多少株花留在原地。
输入输出格式
输入格式:
输入文件为 flower .in。
输入的第一行包含一个整数n,表示开始时花的株数。
第二行包含n个整数,依次为h1,h2..hn,表示每株花的高度。
输出格式:
输出文件为 flower .out。
输出一行,包含一个整数m,表示最多能留在原地的花的株数。
输入输出样例
5 5 3 2 1 2
3
说明
【输入输出样例说明】
有多种方法可以正好保留 3 株花,例如,留下第 1、4、5 株,高度分别为 5、1、2,满
足条件 B。
【数据范围】
对于 20%的数据,n ≤ 10;
对于 30%的数据,n ≤ 25;
对于 70%的数据,n ≤ 1000,0 ≤ ℎi≤ 1000;
对于 100%的数据,1 ≤ n ≤ 100,000,0 ≤ hi≤ 1,000,000,所有的hi 随机生成,所有随机数服从某区间内的均匀分布。
将花的高度用电、线画出来
最大保留值=拐点+1
第一个点开始先向上还是先向下分开算

#include<cstdio> #include<algorithm> using namespace std; int n,a[100011]; bool up; int ans1,ans2; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); a[0]=0x7fffffff; for(int i=1;i<=n;i++) { if(!up&&a[i]>a[i-1]) { ans1++; up=true; } else if(up&&a[i]<a[i-1]) { ans1++; up=false; } } up=true; a[0]=-1; for(int i=1;i<=n;i++) { if(up&&a[i]<a[i-1]) { ans2++; up=false; } else if(!up&&a[i]>a[i-1]) { ans2++; up=true; } } printf("%d",max(ans1,ans2)+1); }
T3 华容道
题目描述
【问题描述】
小 B 最近迷上了华容道,可是他总是要花很长的时间才能完成一次。于是,他想到用编程来完成华容道:给定一种局面, 华容道是否根本就无法完成,如果能完成, 最少需要多少时间。
小 B 玩的华容道与经典的华容道游戏略有不同,游戏规则是这样的:
-
在一个 n*m 棋盘上有 n*m 个格子,其中有且只有一个格子是空白的,其余 n*m-1个格子上每个格子上有一个棋子,每个棋子的大小都是 1*1 的;
-
有些棋子是固定的,有些棋子则是可以移动的;
- 任何与空白的格子相邻(有公共的边)的格子上的棋子都可以移动到空白格子上。
游戏的目的是把某个指定位置可以活动的棋子移动到目标位置。
给定一个棋盘,游戏可以玩 q 次,当然,每次棋盘上固定的格子是不会变的, 但是棋盘上空白的格子的初始位置、 指定的可移动的棋子的初始位置和目标位置却可能不同。第 i 次
玩的时候, 空白的格子在第 EXi 行第 EYi 列,指定的可移动棋子的初始位置为第 SXi 行第 SYi列,目标位置为第 TXi 行第 TYi 列。
假设小 B 每秒钟能进行一次移动棋子的操作,而其他操作的时间都可以忽略不计。请你告诉小 B 每一次游戏所需要的最少时间,或者告诉他不可能完成游戏。
输入输出格式
输入格式:
输入文件为 puzzle.in。
第一行有 3 个整数,每两个整数之间用一个空格隔开,依次表示 n、m 和 q;
接下来的 n 行描述一个 n*m 的棋盘,每行有 m 个整数,每两个整数之间用一个空格隔开,每个整数描述棋盘上一个格子的状态,0 表示该格子上的棋子是固定的,1 表示该格子上的棋子可以移动或者该格子是空白的。接下来的 q 行,每行包含 6 个整数依次是 EXi、EYi、SXi、SYi、TXi、TYi,每两个整数之间用一个空格隔开,表示每次游戏空白格子的位置,指定棋子的初始位置和目标位置。
输出格式:
输出文件名为 puzzle.out。
输出有 q 行,每行包含 1 个整数,表示每次游戏所需要的最少时间,如果某次游戏无法完成目标则输出−1。
输入输出样例
3 4 2 0 1 1 1 0 1 1 0 0 1 0 0 3 2 1 2 2 2 1 2 2 2 3 2
2 -1
说明
【输入输出样例说明】
棋盘上划叉的格子是固定的,红色格子是目标位置,圆圈表示棋子,其中绿色圆圈表示目标棋子。
- 第一次游戏,空白格子的初始位置是 (3, 2)(图中空白所示),游戏的目标是将初始位置在(1, 2)上的棋子(图中绿色圆圈所代表的棋子)移动到目标位置(2, 2)(图中红色的格子)上。
移动过程如下:
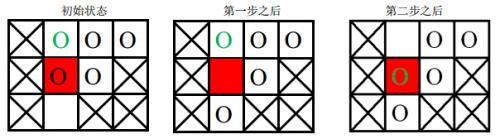
- 第二次游戏,空白格子的初始位置是(1, 2)(图中空白所示),游戏的目标是将初始位置在(2, 2)上的棋子(图中绿色圆圈所示)移动到目标位置 (3, 2)上。
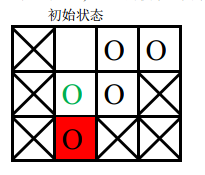
要将指定块移入目标位置,必须先将空白块移入目标位置,空白块要移动到目标位置,必然是从位置(2, 2)上与当前图中目标位置上的棋子交换位置,之后能与空白块交换位置的只有当前图中目标位置上的那个棋子,因此目标棋子永远无法走到它的目标位置, 游戏无
法完成。
【数据范围】
对于 30%的数据,1 ≤ n, m ≤ 10,q = 1;
对于 60%的数据,1 ≤ n, m ≤ 30,q ≤ 10;
对于 100%的数据,1 ≤ n, m ≤ 30,q ≤ 500。
50分暴力法:
bfs跟踪空白块,找所有的可移动的方案,直至到达目标状态
bfs判重方式:将整个棋盘转化为字符串
发现,若空白块与指定块都在同一位置,其他的可移动的块 无论怎么移,都是没用的
所以只需要记录空白块与指定块的位置,就够了
所以80分暴力法:
bfs跟踪空白块,找所有的可移动的方案,直至到达目标状态
bfs判重方式:用mp[i][j][k][l]表示空白块在(i,j),指定块在(k,l)
它的局限性在于
搜索是盲目的,产生大量无用状态
进一步思考,
只有空白块与指定块相邻时,状态才是有用的
所以,由此得出AC做法:
1、预处理所有的有用状态
对于1个指定块和一个空白块,有4种有效状态:空白块分别在指定块的上、下、左、右
对于每一种有效状态,有4种后继状态:另外3个方向的状态、交换空白块与指定块
枚举每一个指定块、再枚举指定块的每一个有效状态,bfs计算 到每一个后继状态的 最小步数
由有效状态 向 后继状态 连权值为 最小步数的边
这样我们就构出了一张图
2、对于每一个初始局面,bfs 算出 空白块 与 指定块 之间有效状态的 步数
也就是 算出 空白块 移到 指定块四周 的步数
3、将第2步算出的 结果作为初始值,在第1步构出的图中跑最短路
如何简介的表示状态?
我的方法;
用0,1,2,3分别表示上右下左
状态=((行号-1)*列数+(列号-1))*4+ 0/1/2/3
看不懂的话,带两个格的8种有效状态手算
由此可得,不断的减少状态数,是优化bfs的一种方法
AC代码:

#include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; int n,m,p; bool a[32][32],v[3601]; int x[4]={-1,0,1,0}; int y[4]={0,1,0,-1}; int pre_dis[32][32],dis[3601]; int front[3601],to[3601*5],nextt[3601*5],w[3601*5],tot; void add(int u,int v,int val) { to[++tot]=v; nextt[tot]=front[u]; front[u]=tot; w[tot]=val; } struct node { int x,y; }nxt,cur; queue<node>q; queue<int>k; int turn(int i,int j) { return (i-1)*m+j-1<<2; } void bfs(int ex,int ey,int px,int py,int d) { int cx,cy,nx,ny; memset(pre_dis,-1,sizeof(pre_dis)); pre_dis[px][py]=1; pre_dis[ex][ey]=0; cur.x=ex;cur.y=ey; q.push(cur); while(!q.empty()) { cur=q.front(); q.pop(); cx=cur.x,cy=cur.y; for(int i=0;i<4;i++) { nx=cur.x+x[i],ny=cur.y+y[i]; if(a[nx][ny]&&pre_dis[nx][ny]==-1) { pre_dis[nx][ny]=pre_dis[cx][cy]+1; nxt.x=nx; nxt.y=ny; q.push(nxt); } } } if(d==4) return; int tmp=turn(px,py); for(int i=0;i<4;i++) if(pre_dis[px+x[i]][py+y[i]]>0) add(tmp+d,tmp+i,pre_dis[px+x[i]][py+y[i]]); add(tmp+d,turn(ex,ey)+(d+2)%4,1); } void spfa(int sx,int sy) { int tmp; memset(dis,-1,sizeof(dis)); for(int i=0;i<4;i++) if(pre_dis[sx+x[i]][sy+y[i]]!=-1) { tmp=turn(sx,sy)+i; dis[tmp]=pre_dis[sx+x[i]][sy+y[i]]; k.push(tmp); } int now; while(!k.empty()) { now=k.front(); k.pop(); v[now]=false; for(int i=front[now];i;i=nextt[i]) if(dis[to[i]]==-1||dis[to[i]]>dis[now]+w[i]) { dis[to[i]]=dis[now]+w[i]; if(!v[to[i]]) { v[to[i]]=true; k.push(to[i]); } } } } int main() { scanf("%d%d%d",&n,&m,&p); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&a[i][j]); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(a[i][j]) { if(a[i-1][j]) bfs(i-1,j,i,j,0); if(a[i][j+1]) bfs(i,j+1,i,j,1); if(a[i+1][j]) bfs(i+1,j,i,j,2); if(a[i][j-1]) bfs(i,j-1,i,j,3); } int ex,ey,sx,sy,tx,ty,ans; while(p--) { scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty); if(sx==tx&&sy==ty) { printf("0\n"); continue; } bfs(ex,ey,sx,sy,4); spfa(sx,sy); ans=0x7fffffff; int tmp=turn(tx,ty); for(int i=0;i<4;i++) if(dis[tmp+i]!=-1) ans=min(ans,dis[tmp+i]); if(ans==0x7fffffff) ans=-1; printf("%d\n",ans); } }
80分暴力代码:(洛谷上70)

#include<iostream> #include<cstring> #include<cstdio> #include<queue> using namespace std; int n,m,p; bool a[32][32],mp[32][32][32][32]; int ex,ey,sx,sy,tx,ty; int cx,cy,nx,ny; int x[4]={-1,0,1,0}; int y[4]={0,1,0,-1}; struct node { int emx,emy,stx,sty,step; }cur,nxt; queue<node>q; void bfs() { while(!q.empty()) q.pop(); cur.emx=ex; cur.emy=ey; cur.step=0; cur.stx=sx; cur.sty=sy; q.push(cur); while(!q.empty()) { cur=q.front(); q.pop(); cx=cur.emx; cy=cur.emy; for(int i=0;i<4;i++) { nx=cx+x[i]; ny=cy+y[i]; if(a[nx][ny]) { if(nx==cur.stx&&ny==cur.sty) nxt.stx=cur.emx,nxt.sty=cur.emy; else nxt.stx=cur.stx,nxt.sty=cur.sty; if(nxt.stx==tx&&nxt.sty==ty) { printf("%d\n",cur.step+1); return; } if(!mp[nx][ny][nxt.stx][nxt.sty]) { mp[nx][ny][nxt.stx][nxt.sty]=true; nxt.emx=nx; nxt.emy=ny; nxt.step=cur.step+1; q.push(nxt); } } } } printf("-1\n"); return; } int main() { freopen("PuzzleNOIP2013.in","r",stdin); freopen("PuzzleNOIP2013.out","w",stdout); scanf("%d%d%d",&n,&m,&p); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&a[i][j]); while(p--) { scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty); if(sx==tx&&sy==ty) { printf("0\n"); continue; } memset(mp,0,sizeof(mp)); mp[ex][ey][sx][sy]=true; bfs(); } }
50分暴力代码:

#include<iostream> #include<cstring> #include<cstdio> #include<queue> #include<map> using namespace std; int n,m,p; bool a[32][32]; int ex,ey,sx,sy,tx,ty,d1,d2; string s,tmp; int cx,cy,nx,ny; int x[4]={-1,0,1,0}; int y[4]={0,1,0,-1}; struct node { string k; int x,y,step; }cur,nxt; queue<node>q; map<string,bool>mp; int turn(int i,int j) { return (i-1)*m+j-1; } void bfs() { mp.clear(); while(!q.empty()) q.pop(); cur.k=s; cur.x=ex; cur.y=ey; cur.step=0; q.push(cur); mp[s]=true; while(!q.empty()) { cur=q.front(); q.pop(); cx=cur.x; cy=cur.y; for(int i=0;i<4;i++) { nx=cx+x[i]; ny=cy+y[i]; if(a[nx][ny]) { d1=turn(cx,cy); d2=turn(nx,ny); if(cx==tx&&cy==ty&&cur.k[turn(nx,ny)]=='3') { printf("%d\n",cur.step+1); return; } swap(cur.k[d1],cur.k[d2]); if(!mp[cur.k]) { nxt.k=cur.k; mp[nxt.k]=true; nxt.x=nx; nxt.y=ny; nxt.step=cur.step+1; q.push(nxt); } swap(cur.k[d1],cur.k[d2]); } } } printf("-1\n"); return; } int main() { freopen("PuzzleNOIP2013.in","r",stdin); freopen("PuzzleNOIP2013.out","w",stdout); scanf("%d%d%d",&n,&m,&p); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { scanf("%d",&a[i][j]); if(a[i][j]) tmp+='1'; else tmp+='0'; } while(p--) { s=tmp; scanf("%d%d%d%d%d%d",&ex,&ey,&sx,&sy,&tx,&ty); s[turn(ex,ey)]='2'; s[turn(sx,sy)]='3'; bfs(); } }
开始的时候写得50分暴力,
只得30分,因为bfs到达目标状态后返回主函数,此时队列里可能还未清空
下一次使用这个队列的时候出错
80分暴力开始得60,
原因:代码不能处理指定块就是目标块的情况


