NOIP2011 提高组 Day2

自测时间：2017.4.12 8:15——11:45

实际得分：100+0+0=100

期望得分：100+100+0=260

T2 符合要求的总价值*符合要求的总个数

写成：符合要求的总价值*区间总个数

T3 正解贪心，DP式子退错了

http://cogs.pro/cogs/page/page.php?aid=16

T1 计算系数

时间限制：1 s 内存限制：128 MB

【问题描述】
给定一个多项式

factor.in

1 1 3 1 2

factor.out

【数据范围】
对于 30%的数据，有

#include<cstdio>
#define mod 10007
int a,b,k,n,m,ans=1;
int f[1011][1011];
using namespace std;
void mul(int a,int b)
{
    a%=mod; b%=mod;
    for(;b;b>>=1,a=a*a%mod)
     if(b&1) ans=ans*a%mod;
}
int main()
{
    freopen("factor.in","r",stdin);
    freopen("factor.out","w",stdout);
    scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
    for(int i=1;i<=k+1;i++) f[i][0]=1;
    for(int i=1;i<=k+1;i++)
     for(int j=1;j<=m;j++)
      f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;
    mul(a,n);
    mul(b,m);
    ans=ans*f[k+1][m]%mod;
    printf("%d",ans);
}
#include<cstdio>
#define mod 10007
int a,b,k,n,m,ans=1;
int f[1011][1011];
using namespace std;
void mul(int a,int b)
{
    a%=mod; b%=mod;
    for(;b;b>>=1,a=a*a%mod)
     if(b&1) ans=ans*a%mod;
}
int main()
{
    freopen("factor.in","r",stdin);
    freopen("factor.out","w",stdout);
    scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
    for(int i=1;i<=k+1;i++) f[i][0]=1;
    for(int i=1;i<=k+1;i++)
     for(int j=1;j<=m;j++)
      f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;
    mul(a,n);
    mul(b,m);
    ans=ans*f[k+1][m]%mod;
    printf("%d",ans);
}

View Code

T2 聪明的质检员

时间限制：1 s 内存限制：128 MB

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 n 个矿石，从 1到n 逐一编号，每个矿石都有自己的重量 wi 以及价值vi 。检验矿产的流程是：

1 、给定m 个区间[Li,Ri]；

2 、选出一个参数 W；

3 、对于一个区间[Li,Ri]，计算矿石在这个区间上的检验值Yi：

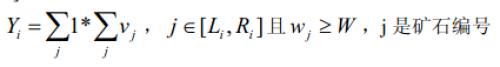
这批矿产的检验结果Y 为各个区间的检验值之和。即：Y1+Y2...+Ym

若这批矿产的检验结果与所给标准值S 相差太多，就需要再去检验另一批矿产。小T

不想费时间去检验另一批矿产，所以他想通过调整参数W 的值，让检验结果尽可能的靠近

标准值S，即使得S-Y 的绝对值最小。请你帮忙求出这个最小值。

输入输出格式

输入格式：

输入文件qc.in 。

第一行包含三个整数n，m，S，分别表示矿石的个数、区间的个数和标准值。

接下来的n 行，每行2个整数，中间用空格隔开，第i+1 行表示 i 号矿石的重量 wi 和价值vi。

接下来的m 行，表示区间，每行2 个整数，中间用空格隔开，第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。注意：不同区间可能重合或相互重叠。

输出格式：

输出文件名为qc.out。

输出只有一行，包含一个整数，表示所求的最小值。

输入输出样例

输入样例#1：

输出样例#1：

说明

【输入输出样例说明】

当W 选4 的时候，三个区间上检验值分别为 20、5 、0 ，这批矿产的检验结果为 25，此

时与标准值S 相差最小为10。

【数据范围】

对于10% 的数据，有 1 ≤n ，m≤10；

对于30% 的数据，有 1 ≤n ，m≤500 ；

对于50% 的数据，有 1 ≤n ，m≤5,000；

对于70% 的数据，有 1 ≤n ，m≤10,000 ；

对于100%的数据，有 1 ≤n ，m≤200,000，0 < wi, vi≤10^6，0 < S≤10^12，1 ≤Li ≤Ri ≤n 。

检验结果随w的减小而增大，所以二分w判断检验结果与标准值的关系

#include<cmath>
#include<cstdio>
#include<algorithm>
#define N 200001
using namespace std;
int n,m,maxn;
long long s,sum[N];
int w[N],v[N],a[N],b[N],tot[N];
long long check(int k)
{
    long long tmp=0;
    for(int i=1;i<=n;i++)
     if(w[i]>=k) sum[i]=sum[i-1]+v[i],tot[i]=tot[i-1]+1;
     else sum[i]=sum[i-1],tot[i]=tot[i-1];
    for(int i=1;i<=m;i++)
     tmp+=abs(sum[b[i]]-sum[a[i]-1])*(tot[b[i]]-tot[a[i]-1]);
    return tmp;
}
int main()
{
    scanf("%d%d",&n,&m);
    scanf("%lld",&s);
    for(int i=1;i<=n;i++) scanf("%d%d",&w[i],&v[i]),maxn=max(maxn,w[i]);
    for(int i=1;i<=m;i++) scanf("%d%d",&a[i],&b[i]);
    int l=0,r=maxn,mid;
    long long ans1=1e15,ans2=1e15,tmp;
    while(l<=r)
    {
        mid=l+r>>1;
        tmp=check(mid);
        if(tmp<s) { ans1=s-tmp;r=mid-1; }
        else if(tmp==s) { printf("0"); return 0; }
        else { ans2=tmp-s; l=mid+1; }
    }
    printf("%lld",min(ans1,ans2));
}

View Code

T3 观光公交

时间限制：1 s 内存限制：128 MB

【问题描述】

风景迷人的小城Y 市，拥有n 个美丽的景点。由于慕名而来的游客越来越多，Y 市特意安排了一辆观光公交车，为游客提供更便捷的交通服务。观光公交车在第0 分钟出现在1号景点，随后依次前往2、3、4……n 号景点。从第i 号景点开到第i+1 号景点需要Di 分钟。
任意时刻，公交车只能往前开，或在景点处等待。
设共有m 个游客，每位游客需要乘车1 次从一个景点到达另一个景点，第i 位游客在Ti 分钟来到景点Ai，希望乘车前往景点Bi（Ai＜bi）。为了使所有乘客都能顺利到达目的地，公交车在每站都必须等待需要从该景点出发的所有乘客都上车后才能出发开往下一景点。
假设乘客上下车不需要时间。
一个乘客的旅行时间，等于他到达目的地的时刻减去他来到出发地的时刻。因为只有一辆观光车，有时候还要停下来等其他乘客，乘客们纷纷抱怨旅行时间太长了。于是聪明的司机ZZ 给公交车安装了k 个氮气加速器，每使用一个加速器，可以使其中一个Di 减1。对于同一个Di 可以重复使用加速器，但是必须保证使用后Di 大于等于0。
那么ZZ 该如何安排使用加速器，才能使所有乘客的旅行时间总和最小？

【输入】

输入文件名为bus.in。

第1 行是3 个整数n, m, k，每两个整数之间用一个空格隔开。分别表示景点数、乘客数和氮气加速器个数。

第2 行是n-1 个整数，每两个整数之间用一个空格隔开，第i 个数表示从第i 个景点开往第i+1 个景点所需要的时间，即Di。

第3 行至m+2 行每行3 个整数Ti, Ai, Bi，每两个整数之间用一个空格隔开。第i+2 行表示第i 位乘客来到出发景点的时刻，出发的景点编号和到达的景点编号。

【输出】

输出文件名为bus.out。共一行，包含一个整数，表示最小的总旅行时间。

【输入输出样例】

3 3 2

1 4

0 1 3

1 1 2

5 2 3

输出：10

【输入输出样例说明】

对D2 使用2 个加速器，从2 号景点到3 号景点时间变为2 分钟。

公交车在第1 分钟从1 号景点出发，第2 分钟到达2 号景点，第5 分钟从2 号景点出发，第7 分钟到达3 号景点。

第1 个旅客旅行时间 7-0 = 7 分钟。

第2 个旅客旅行时间 2-1 = 1 分钟。

第3 个旅客旅行时间 7-5 = 2 分钟。

总时间 7+1+2 = 10 分钟。

【数据范围】

对于10%的数据，k=0；

对于20%的数据，0<=k<=1。

对于40%的数据，2 ≤ n ≤ 50，1 ≤ m≤ 1,000，0 ≤ k ≤ 20，0 ≤ Di ≤ 10，0 ≤ Ti ≤ 500；

对于60%的数据，1 ≤ n ≤ 100，1 ≤ m≤ 1,000，0 ≤ k ≤ 100，0 ≤ Di ≤ 100，0 ≤ Ti ≤ 10,000；

对于100%的数据，1 ≤ n ≤ 1,000，1 ≤ m ≤ 10,000，0 ≤ k ≤ 100,000，0 ≤ Di ≤ 100，0 ≤ Ti ≤ 100,000。

汽车最早到达景点i的时间get[i],

景点i最后一个游客出现时间last[i]

那么ans=Σ（get[b[i]]-t[i]）=Σ get[b[i]]-Σt[i]

Σt[i]是定值，所以要最小化Σ get[b[i]]

d[i]表示从景点i-1到i所需时间

先算出不使用加速器的get ：get[i]=max（get[i-1],last[i-1]）+d[i]

（从上一个景点的出发时间=到达上一个景点的时间、上一个经典游客的最晚出现时间中较大的）

使用1个加速器可以令答案减少影响人数*1

所以枚举加速器，贪心的用了加速器后影响人数最多的地方

sum[i]表示在景点i下车的人数

data[i]表示在景点i-1到景点i使用加速器可以影响的人数

初始data[i]=sum[i]

然后倒序枚举景点，若last[i]<get[i]，（最后一个游客出现的时间比汽车到达时间早）

data[i]+=data[i+1]

然后找到最大的data[i]，d[i]--，更新get[]

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,k;
int t[10001],a[10001],b[10001],d[1001],data[1001];
int gett[1001],last[1001],sum[1001],g[1001],ans;
int main()
{
    /*freopen("bus.in","r",stdin);
    freopen("bus.out","w",stdout);*/
    scanf("%d%d%d",&n,&m,&k);
    for(int i=2;i<=n;i++) scanf("%d",&d[i]);
    for(int i=1;i<=m;i++) 
    {
        scanf("%d%d%d",&t[i],&a[i],&b[i]);
        last[a[i]]=max(last[a[i]],t[i]);
        sum[b[i]]++;;
    }
    for(int i=2;i<=n;i++) gett[i]=max(gett[i-1],last[i-1])+d[i];
    //g[n]=n;
    //for(int i=n-1;i>1;i--) g[i]= gett[i]>last[i] ? g[i+1] : i;
    //for(int i=1;i<=n;i++) sum[i]+=sum[i-1];sum[n+1]=sum[n]+(sum[n]-sum[n-1]);
    for(int i=1;i<=m;i++) ans+=gett[b[i]]-t[i];
    while(k--)
    {
        int maxn=0,tmp=0;
        for(int i=n;i>1;i--) 
        {
            data[i]=sum[i];
            if(last[i]<gett[i]) data[i]+=data[i+1];
        }
        for(int i=2;i<=n;i++) 
         //if(maxn<sum[g[i]+1]-sum[i]&&d[i]>0)
         if(maxn<data[i]&&d[i]>0)
         {
               //maxn=sum[g[i]+1]-sum[i];
               maxn=data[i];
               tmp=i;
         }
        ans-=maxn;
        d[tmp]--;
        for(int i=tmp;i<=n/*g[tmp]*/;i++) gett[i]=max(gett[i-1],last[i-1])+d[i];
        //for(int i=g[tmp];i>=tmp;i--) g[i]= gett[i]>last[i] ? g[i+1] : i;
    }
    printf("%d",ans);
}

View Code

posted @ 2017-04-12 18:00 TRTTG 阅读(711) 评论(0) 编辑收藏举报

刷新页面返回顶部

日拱一卒功不唐捐

一点一滴，未来可期

NOIP2011 提高组 Day2

题目描述

输入输出格式

输入输出样例

说明

【问题描述】

【输入】

【输出】

【输入输出样例】

【数据范围】

公告

日拱一卒 功不唐捐

一点一滴，未来可期

NOIP2011 提高组 Day2

题目描述

输入输出格式

输入输出样例

说明

【问题描述】

【输入】

【输出】

【输入输出样例】

【数据范围】

公告

日拱一卒功不唐捐