NOIP2016 蚯蚓
题目描述
本题中,我们将用符号[c]表示对c向下取整,例如:[3.0」= [3.1」=[3.9」=3。
蛐蛐国最近蚯蚓成灾了!隔壁跳蚤国的跳蚤也拿蚯蚓们没办法,蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。
蛐蛐国里现在共有n只蚯蚓(n为正整数)。每只蚯蚓拥有长度,我们设第i只蚯蚓的长度为a_i(i=1,2,...,n),并保证所有的长度都是非负整数(即:可能存在长度为0的蚯蚓)。
每一秒,神刀手会在所有的蚯蚓中,准确地找到最长的那一只(如有多个则任选一个)将其切成两半。神刀手切开蚯蚓的位置由常数p(是满足0<p<1的有理数)决定,设这只蚯蚓长度为x,神刀手会将其切成两只长度分别为[px]和x-[px]的蚯蚓。特殊地,如果这两个数的其中一个等于0,则这个长度为0的蚯蚓也会被保留。此外,除了刚刚产生的两只新蚯蚓,其余蚯蚓的长度都会增加q(是一个非负整常数)。
蛐蛐国王知道这样不是长久之计,因为蚯蚓不仅会越来越多,还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物,但是救兵还需要m秒才能到来......
(m为非负整数)
蛐蛐国王希望知道这m秒内的战况。具体来说,他希望知道:
•m秒内,每一秒被切断的蚯蚓被切断前的长度(有m个数)
•m秒后,所有蚯蚓的长度(有n+m个数)。
蛐蛐国王当然知道怎么做啦!但是他想考考你......
输入输出格式
输入格式:
第一行包含六个整数n,m,q,u,v,t,其中:n,m,q的意义见【问题描述】;u,v,t均为正整数;你需要自己计算p=u/v(保证0<u<v)t是输出参数,其含义将会在【输出格式】中解释。
第二行包含n个非负整数,为ai,a2,...,an,即初始时n只蚯蚓的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。
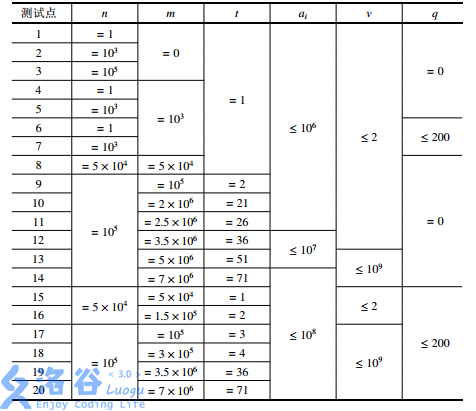
保证1<=n<=10^5,0<m<7*10^6,0<u<v<10^9,0<=q<=200,1<t<71,0<ai<10^8。
输出格式:
第一行输出[m/t]个整数,按时间顺序,依次输出第t秒,第2t秒,第3t秒……被切断蚯蚓(在被切断前)的长度。
第二行输出[(n+m)/t]个整数,输出m秒后蚯蚓的长度;需要按从大到小的顺序,依次输出排名第t,第2t,第3t……的长度。
同一行中相邻的两个数之间,恰好用一个空格隔开。即使某一行没有任何数需要 输出,你也应输出一个空行。
请阅读样例来更好地理解这个格式。
【数据范围】

输入输出样例 输入样例#1: 3 7 1 1 3 1 3 3 2 输出样例#1: 3 4 4 4 5 5 6 6 6 6 5 5 4 4 3 2 2 输入样例#2: 3 7 1 1 3 2 3 3 2 输出样例#2: 4 4 5 6 5 4 3 2 输入样例#3: 3 7 1 1 3 9 3 3 2 输出样例#3: //空行 2 说明 【样例解释1】 在神刀手到来前:3只蚯蚓的长度为3,3,2。 1秒后:一只长度为3的蚯蚓被切成了两只长度分别为1和2的蚯蚓,其余蚯蚓的长度增加了1。最终4只蚯蚓的长度分别为(1,2),4,3。括号表示这个位置刚刚有一只蚯蚓被切断 2秒后:一只长度为4的蚯蚓被切成了1和3。5只蚯蚓的长度分别为:2,3,(1,3),4。 3秒后:一只长度为4的蚯蚓被切断。6只蚯蚓的长度分别为:3,4,2,4,(1,3)。 4秒后:一只长度为4的蚯蚓被切断。7只蚯蚓的长度分别为:4,(1,3),3,5,2,4。 5秒后:一只长度为5的蚯蚓被切断。8只蚯蚓的长度分别为:5,2,4,4,(1,4),3,5。 6秒后:一只长度为5的蚯蚓被切断。9只蚯蚓的长度分别为:(1,4),3,5,5,2,5,4,6。 7秒后:一只长度为6的蚯蚓被切断。10只蚯蚓的长度分别为:2,5,4,6,6,3,6,5,(2,4)。所以,7秒内被切断的蚯蚓的长度依次为3,4,4,4,5,5,6。7秒后,所有蚯蚓长度从大到小排序为6,6,6,5,5,4,4,3,2,2 【样例解释2】 这个数据中只有t=2与上个数据不同。只需在每行都改为每两个数输出一个数即可。 虽然第一行最后有一个6没有被输出,但是第二行仍然要重新从第二个数再开始输出。 【样例解释3】 这个数据中只有t=9与上个数据不同。 注意第一行没有数要输出,但也要输出一个空行。
把x切为两段a,b,切断位置是p=u/v,因为u<v,所以p<1
所以说a和b一定比x小,
所以若x1>x2,x1切出a1,b1,x2切出a2,b2,
那么a1>a2,b1>b2
所以按从大到小的顺序切蚯蚓,切出的所有第一段递减,所有第二段递减
所以开3个队列q1,q2,q3
q1存蚯蚓原长度,q2存所有切出的第一段,q3存第二段
q1 sort降序排列
q2、q3根据前面退出的递减性,按顺序存进去即可
切的时候取3个队列 最大的队首元素x
还有一点
除了刚刚产生的两只新蚯蚓a,b,其余蚯蚓的长度都会增加q
其他蚯蚓增加p相当于a,b减p
所以队列里存相对长度
所以用一个变量gather累加q
判断切取位置时,x+gather
然后gather+=p
往q2,q3里存a-gather,b-gather
问:为什么a,b减得gather要先加p?
因为x之前加了gather,变为实际长度
所以a,b也是实际长度
要先减去这一次切之前的累加,
然后这一次切 a,b要-p
所以gather先累加p
#include<cstdio> #include<algorithm> #include<iostream> #include<cmath> #include<cstring> #define N 100002 #define M 7000002 using namespace std; int q1[N],q2[M],q3[M]; int h1,h2,h3,t1,t2,t3; double p; int gather; int main() { int n,m,q,u,v,t; memset(q1,-127,sizeof(q1)); memset(q2,-127,sizeof(q2)); memset(q3,-127,sizeof(q3)); scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t); p=(double)u/(double)v; for(int i=1;i<=n;i++) scanf("%d",&q1[i]); sort(q1+1,q1+n+1,greater<int>()); h1=h2=h3=1;t1=n; int x,y,z; for(int i=1;i<=m;i++) { x=max(max(q1[h1],q2[h2]),q3[h3]); if(q1[h1]==x) h1++; else if(q2[h2]==x) h2++; else h3++; x+=gather; y=floor(p*x); z=x-y; gather+=q; q2[++t2]=y-gather; q3[++t3]=z-gather; if(i%t==0) printf("%d ",x); } printf("\n"); for(int i=1;i<=n+m;i++) { x=max(max(q1[h1],q2[h2]),q3[h3]); if(q1[h1]==x) h1++; else if(q2[h2]==x) h2++; else h3++; x+=gather; if(i%t==0) printf("%d ",x); } }



