bzoj 2683: 简单题（CDQ分治）

2683: 简单题

Time Limit: 50 Sec  Memory Limit: 128 MB

Description

你有一个N*N的棋盘，每个格子内有一个整数，初始时的时候全部为0，现在需要维护两种操作：

 

命令

参数限制

内容

1 x y A

1<=x,y<=N，A是正整数

将格子x,y里的数字加上A

2 x1 y1 x2 y2

1<=x1<= x2<=N

1<=y1<= y2<=N

输出x1 y1 x2 y2这个矩形内的数字和

3

无

终止程序

Input

输入文件第一行一个正整数N。
接下来每行一个操作。

Output

对于每个2操作，输出一个对应的答案。

Sample Input

4
1 2 3 3
2 1 1 3 3
1 2 2 2
2 2 2 3 4
3

Sample Output

3
5

HINT

1<=N<=500000,操作数不超过200000个，内存限制20M。

对于100%的数据，操作1中的A不超过2000。
题目空间限制有歧义，实际评测空间是128M
对于修改操作，直接改就行
对于查询操作，看图
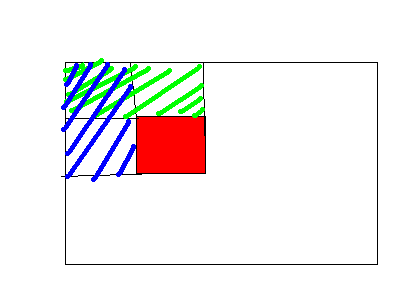
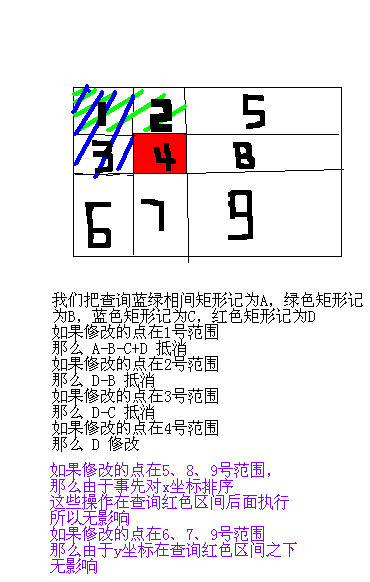
查询红色部分的和，用左上角整个矩形-绿色的-蓝色的+蓝绿相间的即可
用CDQ分治
那就需要控制操作时间t、操作x、y坐标三者的关系
x坐标可以排序
操作时间t可以分治过程中控制
那么y呢？
我们可以直接用树状数组维护y坐标那一整行的信息
//代码中对所有坐标都后移一位
//因为最初想到树状数组不能使用下标为0的点
//但是不让本题只有查询操作坐标才-1
//而查询操作的前提是x>0
//所以坐标不用后移 
#include<cstdio>
#include<algorithm>
#define M 200010
#define N 500010
using namespace std;
int n,tot,cnt;
int tr[N],ans[M];
struct node
{
    int x,y,key,t,kind,bl;
}q[M*4],tmp[M*4];
bool cmp(node k,node l)
{
    if(k.x!=l.x) return k.x<l.x;
    if(k.y!=l.y) return k.y<l.y;
    return k.kind<l.kind;
}
int lowbit(int x)
{
    return x&(-x);
}
void add(int x,int k)
{
    //while(x<=n+1)
    while(x<=n) 
    {
        tr[x]+=k;
        x+=lowbit(x);
    }
}
int sum(int x)
{
    int a=0;
    while(x)
    {
        a+=tr[x];
        x-=lowbit(x);
    }
    return a;
}
void solve(int l,int r)
{
    if(l==r) return;
    int mid=l+r>>1,ll=l,rr=mid+1;
    for(int i=l;i<=r;i++)
    {
        if(q[i].t<=mid&&q[i].kind==1) add(q[i].y,q[i].key);
        else if(q[i].t>mid&&q[i].kind==2) ans[q[i].bl]+=q[i].key*sum(q[i].y);
    }
    for(int i=l;i<=r;i++)
     if(q[i].t<=mid&&q[i].kind==1) add(q[i].y,-q[i].key);//目的：清空树状数组
    for(int i=l;i<=r;i++)
    {
        if(q[i].t<=mid) tmp[ll++]=q[i];
        else tmp[rr++]=q[i];
    }
    for(int i=l;i<=r;i++) q[i]=tmp[i];
    solve(l,mid);solve(mid+1,r);
}
int main()
{
    scanf("%d",&n);
    int x1,y1,z,x2,y2;
    while(1)
    {
        scanf("%d",&z);
        if(z==1)
        {
            scanf("%d%d%d",&x1,&y1,&z);
            //x1++;y1++;
            q[++tot]=(node){x1,y1,z,tot,1,0};
        }
        else if(z==2)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            //x1++;y1++;x2++;y2++;
            cnt++;
            q[++tot]=(node){x1-1,y1-1,1,tot,2,cnt};
            q[++tot]=(node){x1-1,y2,-1,tot,2,cnt};
            q[++tot]=(node){x2,y1-1,-1,tot,2,cnt};
            q[++tot]=(node){x2,y2,1,tot,2,cnt};
        }
        else break;
    }
    sort(q+1,q+tot+1,cmp);
    solve(1,tot);
    for(int i=1;i<=cnt;i++) printf("%d\n",ans[i]);
}

 

posted @ 2017-03-13 20:42  TRTTG  阅读(328)  评论(0)  编辑  收藏  举报