[HNOI 2013]切糕

COGS 2398. [HNOI 2013]切糕

http://www.cogs.pro/cogs/problem/problem.php?pid=2398

★★★☆   输入文件：nutcake.in   输出文件：nutcake.out   简单对比
时间限制：5 s   内存限制：512 MB

[HNOI 2013]切糕

第三题：切糕（程序文件名：cake.exe）100 分，运行时限：5s

经过千辛万苦小A 得到了一块切糕，切糕的形状是长方体，小A 打算拦腰将切糕切成两半分给小B。出于美观考虑，小A 希望切面能尽量光滑且和谐。于是她找到你，希望你能帮她找出最好的切割方案。

出于简便考虑，我们将切糕视作一个长P、宽Q、高R 的长方体点阵。我们将位于第z层中第x 行、第y 列上(1≤x≤P, 1≤y≤Q, 1≤z≤R)的点称为(x,y,z)，它有一个非负的不和谐值v(x,y,z)。一个合法的切面满足以下两个条件：

1. 与每个纵轴(一共有P*Q 个纵轴)有且仅有一个交点。即切面是一个函数f(x,y)，对于所有1≤x≤P, 1≤y≤Q,我们需指定一个切割点f(x,y),且1≤f(x,y)≤R。

2. 切面需要满足一定的光滑性要求，即相邻纵轴上的切割点不能相距太远。对于所有的1≤x,x’≤P 和1≤y,y’ ≤Q，若|x-x’|+|y-y’|=1，则|f(x,y)-f(x’,y’)| ≤D，其中D 是给定的一个非负整数。

可能有许多切面f 满足上面的条件，小A 希望找出总的切割点上的不和谐值最小的那个，即v(x, y, f (x, y))x,y 最小。

【输入格式】（input.txt）

从文件input.txt中读入数据，输入文件第一行是三个正整数P,Q,R，表示切糕的长P、宽Q、高R。第二行有一个非负整数D，表示光滑性要求。接下来是R个P行Q列的矩阵，第z个矩阵的第x行第y列是v(x,y,z) (1≤x≤P,1≤y≤Q, 1≤z≤R)。

100%的数据满足P,Q,R≤40，0≤D≤R，且给出的所有的不和谐值不超过1000。

【输出格式】（output.txt）

输出文件output.txt 仅包含一个整数，表示在合法基础上最小的总不和谐值。

【输入输出样例】

input.txt       output.txt

2 2 2            6

1

6 1

6 1

2 6

2 6

input.txt   output.txt

2 2 2        12

0

5 1

5 1

2 5

2 5

【样例解释】

第一组样例中最佳切面的f为f(1,1)=f(2,1)=2,f(1,2)=f(2,2)=1。

第二组样例中最佳切面的f为f(1,1)=f(2,1)=f(1,2)=f(2,2)=1。

最小割 

让图来说话（画得有点儿丑、大佬勿喷）

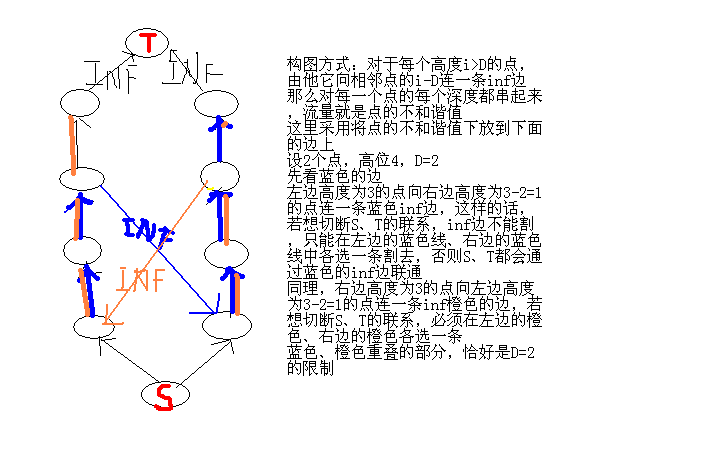
#include<cstdio>
#include<queue>
#define N 70000
#define M 12*N
#define inf 1e9
using namespace std;
int p,q,r,d;
int f[41][41][41];
int dx[4]={-1,0,1,0};
int dy[4]={0,1,0,-1};
int tot=1,ans;
int src,dec;
int front[N],nextt[M],to[M],cap[M],cnt[M],lev[N]; 
queue<int>qq; 
void insert(int u,int v,int w) 
{ 
    to[++tot]=v;cap[tot]=w;nextt[tot]=front[u];front[u]=tot; 
    to[++tot]=u;cap[tot]=0;nextt[tot]=front[v];front[v]=tot; 
} 
bool bfs() 
{ 
    for(int i=0;i<=dec;i++) {cnt[i]=front[i];lev[i]=-1;} 
    while(!qq.empty()) qq.pop(); 
    qq.push(src);lev[src]=0; 
    while(!qq.empty()) 
    { 
        int now=qq.front();qq.pop(); 
        for(int i=front[now];i!=0;i=nextt[i]) 
        { 
            int t=to[i]; 
            if(cap[i]>0&&lev[t]==-1) 
            { 
                qq.push(t); 
                lev[t]=lev[now]+1; 
                if(t==dec) return true; 
            } 
        } 
    } 
    return false; 
} 
int dinic(int now,int flow) 
{ 
    if(now==dec) return flow; 
    int delta,rest=0; 
    for(int & i=cnt[now];i!=0;i=nextt[i]) 
    { 
        int t=to[i]; 
        if(lev[t]==lev[now]+1&&cap[i]>0) 
        { 
            delta=dinic(t,min(cap[i],flow-rest)); 
            if(delta) 
            { 
                cap[i]-=delta;cap[i^1]+=delta; 
                rest+=delta;if(rest==flow) break; 
            } 
        } 
    } 
    if(rest!=flow) lev[now]=-1; 
    return rest; 
} 
int change(int x,int y,int z)
{
    if(!z) return 0;
    return (z-1)*p*q+(x-1)*q+y;
 } 
void build()
{
    for(int i=1;i<=p;i++)
     for(int j=1;j<=q;j++)
      {
          for(int k=1;k<=r;k++)
          {
              insert(change(i,j,k-1),change(i,j,k),f[i][j][k]);
              if(k>d)
              {
                  for(int l=0;l<4;l++)
                  {
                      int nx=i+dx[l],ny=j+dy[l];
                      if(nx>=1&&nx<=p&&ny>=1&&ny<=q)
                       insert(change(i,j,k),change(nx,ny,k-d),inf);
                }
            }
          }
        insert(change(i,j,r),dec,inf);
      }
} 
int main()
{
    freopen("nutcake.in","r",stdin);
    freopen("nutcake.out","w",stdout);
    scanf("%d%d%d%d",&p,&q,&r,&d);
    dec=p*q*r+1;
    for(int i=1;i<=r;i++)
     for(int j=1;j<=p;j++)
      for(int k=1;k<=q;k++)
          scanf("%d",&f[j][k][i]);
    build();
    while(bfs()) ans+=dinic(src,inf); 
    printf("%d",ans);
}