(noi.openjudge.cn) 1.8编程基础之多维数组T21——T25
T21 二维数组右上左下遍历
描述
给定一个row行col列的整数数组array,要求从array[0][0]元素开始,按从左上到右下的对角线顺序遍历整个数组。

输入
输入的第一行上有两个整数,依次为row和col。
余下有row行,每行包含col个整数,构成一个二维整数数组。
(注:输入的row和col保证0 < row < 100, 0 < col < 100)
输出
按遍历顺序输出每个整数。每个整数占一行。

样例输入 3 4 1 2 4 7 3 5 8 10 6 9 11 12 样例输出 1 2 3 4 5 6 7 8 9 10 11 12
先枚举第一行,向左下枚举,再枚举最后一列(除去右上角,因为第一行已经枚举过了)

1 #include<iostream> 2 using namespace std; 3 int n,m,a[101][101]; 4 int main() 5 { 6 cin>>n>>m; 7 for(int i=1;i<=n;i++) 8 for(int j=1;j<=m;j++) 9 cin>>a[i][j]; 10 for(int j=1;j<=m;j++)//枚举第一行 11 { 12 int i=1,k=j;//i:当前行,k:当前列 13 while(i<=n&&k>0)//不超边界 14 { 15 cout<<a[i][k]<<endl; 16 i++;k--; 17 } 18 } 19 for(int i=2;i<=n;i++)//最后一列,从第二行开始 20 { 21 int j=m,k=i;//j:当前列,k:当前行 22 while(k<=n&&j>0)//不超边界 23 { 24 cout<<a[k][j]<<endl; 25 k++;j--; 26 } 27 } 28 }
第一次枚举最后一列时从第一行开始的,0分。。。。。。
T22 神奇的幻方
描述
幻方是一个很神奇的N*N矩阵,它的每行、每列与对角线,加起来的数字和都是相同的。
我们可以通过以下方法构建一个幻方。(阶数为奇数)
1.第一个数字写在第一行的中间
2.下一个数字,都写在上一个数字的右上方:
a.如果该数字在第一行,则下一个数字写在最后一行,列数为该数字的右一列
b.如果该数字在最后一列,则下一个数字写在第一列,行数为该数字的上一行
c.如果该数字在右上角,或者该数字的右上方已有数字,则下一个数字写在该数字的下方
输入
一个数字N(N<=20)
输出
按上方法构造的2N-1 * 2N-1的幻方

样例输入 3 样例输出 17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9
类似于NOIP2015 Day1 T1,但这道题是2*n-1阶的

1 #include<iostream> 2 using namespace std; 3 int n,a[50][50]; 4 int main() 5 { 6 cin>>n; 7 a[1][n]=1; 8 int i=2,x=1,y=n; 9 while(i<=(2*n-1)*(2*n-1)) 10 { 11 if((x==1&&y==2*n-1)||a[x-1][y+1]) x+=1; 12 else if(x==1) x=2*n-1,y+=1; 13 else if(y==2*n-1) x-=1,y=1; 14 else x-=1,y+=1; 15 a[x][y]=i++; 16 } 17 for(int k=1;k<=2*n-1;k++) 18 { 19 for(int l=1;l<=2*n-1;l++) 20 cout<<a[k][l]<<' '; 21 cout<<endl; 22 } 23 }
T23 二维数组回形遍历
描述
给定一个row行col列的整数数组array,要求从array[0][0]元素开始,按回形从外向内顺时针顺序遍历整个数组。如图所示:

输入
输入的第一行上有两个整数,依次为row和col。
余下有row行,每行包含col个整数,构成一个二维整数数组。
(注:输入的row和col保证0 < row < 100, 0 < col < 100)
输出
按遍历顺序输出每个整数。每个整数占一行。

样例输入 4 4 1 2 3 4 12 13 14 5 11 16 15 6 10 9 8 7 样例输出 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
递归遍历即可,一定要注意一个格子只能走一遍以及判断是否输出了所有数,不然会递归死循环

1 #include<iostream> 2 using namespace std; 3 int n,m,a[101][101]; 4 bool v[101][101]; 5 bool ok; 6 bool judge()//判断是否已经输出了所有的数 7 { 8 for(int i=1;i<=n;i++) 9 for(int j=1;j<=m;j++) 10 if(!v[i][j]) return false; 11 return true; 12 } 13 //R向右 ,D向下,L向左,U向上 14 void dfs(int x,int y,char p)//x:当前行,y:当前列,p判断向哪儿走 15 { 16 if(ok) return;//在judge之前先判断是否已经输出了所有点,防止输出完递归回退时多次执行judge函数,浪费时间 17 ok=judge(); 18 if(p=='R')//可以向右走 19 { 20 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y])//不超边界且没有被遍历 21 { 22 cout<<a[x][y]<<endl; 23 v[x][y]=true; 24 dfs(x,y+1,'R');//继续向右走 25 } 26 else p='D',dfs(x+1,y-1,'D');//转为向下走,当执行这个语句时,y已经超出了边界,所以要减1,向下走x+1 27 } 28 else if(p=='D') 29 { 30 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y]) 31 { 32 cout<<a[x][y]<<endl; 33 v[x][y]=true; 34 dfs(x+1,y,'D'); 35 } 36 else p='L',dfs(x-1,y-1,'L'); 37 } 38 else if(p=='L') 39 { 40 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y]) 41 { 42 cout<<a[x][y]<<endl; 43 v[x][y]=true; 44 dfs(x,y-1,'L'); 45 } 46 else p='U',dfs(x-1,y+1,'U'); 47 } 48 else if(p=='U') 49 { 50 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y]) 51 { 52 cout<<a[x][y]<<endl; 53 v[x][y]=true; 54 dfs(x-1,y,'U'); 55 } 56 else p='R',dfs(x+1,y+1,'R'); 57 } 58 } 59 int main() 60 { 61 cin>>n>>m; 62 for(int i=1;i<=n;i++) 63 for(int j=1;j<=m;j++) 64 cin>>a[i][j]; 65 dfs(1,1,'R'); 66 }
T24 蛇形填充数组
描述
用数字1,2,3,4,...,n*n这n2个数蛇形填充规模为n*n的方阵。
蛇形填充方法为:
对于每一条左下-右上的斜线,从左上到右下依次编号1,2,...,2n-1;按编号从小到大的顺序,将数字从小到大填入各条斜线,其中编号为奇数的从左下向右上填写,编号为偶数的从右上到左下填写。
比如n=4时,方阵填充为如下形式:
1 2 6 7 3 5 8 13 4 9 12 14 10 11 15 16
输入
输入一个不大于10的正整数n,表示方阵的行数。
输出
输出该方阵,相邻两个元素之间用单个空格间隔。
注意处理边界情况。
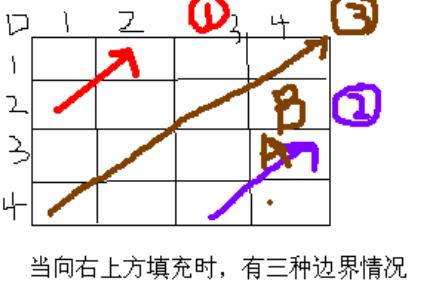
①:超出矩阵上边界,此时位置坐标已经到①出,列与拐弯后的位置的列相等,行少了1,所以行+1,列不变
②:超出矩阵右边界,此时位置坐标已经到②出,行与拐弯后的位置的行少了2行,列多了一列,所以行+2,列-1
③:即超出上边界,又超出右边界,此时位置到③处,我们可以手算一下,若先执行①,再执行②,会到达A处;先执行②,再执行①,会到达B处,而拐弯后的目标位置为B处,所以在程序中,要先判断②的情况,在判断①的情况。
当然为了避免③的情况,也可以另写一个语句直接判断
如果不是边界,直接行减1,列加1
当向左下方填充时,情况类似,就不再写了

1 #include<iostream> 2 using namespace std; 3 int n,a[11][11]; 4 bool ok; 5 int main() 6 { 7 cin>>n; 8 int s=0,p=1; 9 int x=1,y=1; 10 while(s<n*n)//填充,具体解释看上面的题解 11 { 12 while(p%2==0&&s<n*n) 13 { 14 ok=false; 15 s++; 16 a[x][y]=s; 17 x++;y--; 18 if(x>n) x--,y+=2,ok=true; 19 if(y<1) y++,ok=true; 20 if(ok) p++; 21 } 22 while(p%2==1&&s<n*n) 23 { 24 ok=false; 25 s++; 26 a[x][y]=s; 27 x--;y++; 28 if(y>n) x+=2,y--,ok=true; 29 if(x<1) x++,ok=true; 30 if(ok) p++; 31 } 32 } 33 for(int i=1;i<=n;i++) 34 { 35 for(int j=1;j<=n;j++) 36 cout<<a[i][j]<<' '; 37 cout<<endl; 38 } 39 }
一开始没考虑③的情况,先判断的①,在判断的②,导致对角线拐弯时错行
T25 螺旋加密
描述
Chip和Dale发明了一种文本信息加密技术。他们事先秘密约定好矩阵的行数和列数。接着,将字符按如下方式编码:
1. 所有文本只包含大写字母和空格。
2. 每个字符均赋予一个数值:空格=0,A=1,B=2,……,Y=25,Z=26。
按照下图所示的方式,将每个字符对应数值的5位二进制数依次填入矩阵。最后用0将矩阵补充完整。例如,对于信息“ACM”,行列数均为4时,矩阵将被填充为:

将矩阵中的数字按行连起来形成数字串,完成加密。例子中的信息最终会被加密为:0000110100101100。
输入
一行。首先是两个整数R(1≤R≤20)和C(1≤C≤20),表示行数和列数。之后是一个只包含大写字母和空格的字符串。字符串的长度≤(R*C)/5。R和C之间以及C和字符串之间均用单个空格隔开。
输出
一行,为加密后的二进制串。注意你可能需要用0将矩阵补充完整。
先将字符串按要求转化为二进制数字,然后再用类似T23二维数组回形遍历的方法把数字存到矩阵里,最后按顺序输出。这种方法虽然麻烦点儿,但比较快,用时0ms
注意数据的读入方式,为了防止读入多余的空格或少读空格,可以将一整行当字符串用gets读进去,再找空格分开。也可以多输入一个getchar()语句。

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 int n,m,a[101][101]; 6 char s[100]; 7 int ss[1000]; 8 bool v[101][101]; 9 int sum; 10 //R向右 ,D向下,L向左,U向上 11 void dfs(int x,int y,char p)//x:当前行,y:当前列,p判断向哪儿走 12 { 13 if(sum==n*m) return; 14 if(p=='R')//可以向右走 15 { 16 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y])//不超边界且没有被填充 17 { 18 a[x][y]=ss[++sum]; 19 v[x][y]=true; 20 dfs(x,y+1,'R');//继续向右走 21 } 22 else p='D',dfs(x+1,y-1,'D');//转为向下走,当执行这个语句时,y已经超出了边界,所以要减1,向下走x+1 23 } 24 else if(p=='D') 25 { 26 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y]) 27 { 28 a[x][y]=ss[++sum]; 29 v[x][y]=true; 30 dfs(x+1,y,'D'); 31 } 32 else p='L',dfs(x-1,y-1,'L'); 33 } 34 else if(p=='L') 35 { 36 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y]) 37 { 38 a[x][y]=ss[++sum]; 39 v[x][y]=true; 40 dfs(x,y-1,'L'); 41 } 42 else p='U',dfs(x-1,y+1,'U'); 43 } 44 else if(p=='U') 45 { 46 if(x>0&&x<=n&&y>0&&y<=m&&!v[x][y]) 47 { 48 a[x][y]=ss[++sum]; 49 v[x][y]=true; 50 dfs(x-1,y,'U'); 51 } 52 else p='R',dfs(x+1,y+1,'R'); 53 } 54 } 55 int main() 56 { 57 gets(s); 58 int i; 59 for(i=0;i<strlen(s);i++)//取出行 n 60 { 61 if(s[i]!=' ') n=n*10+s[i]-'0'; 62 else break; 63 } 64 int j; 65 for(j=i+1;j<strlen(s);j++)//取出列 m 66 { 67 if(s[j]!=' ') m=m*10+s[j]-'0'; 68 else break; 69 } 70 int l=0; 71 for(int k=j+1;k<strlen(s);k++) //将字符串转化为二进制 72 { 73 if(s[k]==' ')//空格的情况时5个0 74 for(int u=1;u<=5;u++) ss[++l]=0; 75 else 76 { 77 l+=5;//倒着填二进制数 78 int p=s[k]-64,w=0; 79 while(p) 80 { 81 ss[l]=p%2; 82 p/=2; 83 l--; 84 } 85 while(l%5) ss[l]=0,l--;//二进制位数有可能不足5位 86 l+=5;//前面倒着填的再加回去 87 } 88 } 89 for(int k=l+1;k<=n*m;k++) 90 ss[k]=0;//用0将矩阵补充完整 91 dfs(1,1,'R'); 92 for(int p=1;p<=n;p++) 93 for(int k=1;k<=m;k++) 94 cout<<a[p][k]; 95 }
下附简短代码,用时1ms
精简之处1:cin、getchar()与getline()的使用省去上面用gets读入在分离的过程
精简之处2:打表提前打出26个英文字符的二进制,利用c++自带的substr函数省去循环5次存储五位二进制的过程
精简之处3:将二进制数存到矩阵中时,以矩阵的一圈为单位,依次以(1,1)、(2,2)、(3,3)等为起点,用while一圈一圈的存储,而不是dfs
精简之处4:题目要求,用0将矩阵补充完整,全局变量定义数组初始值即为0,可以不用管

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,m,l,c,x,y,t,a[105][105]; 4 string s,ss,q="0000100010000110010000101001100011101000010010101001011011000110101110011111000010001100101001110100101011011010111110001100111010"; 5 int main() 6 { 7 cin>>n>>m; 8 getchar(); 9 getline(cin,s); 10 l=s.size(); 11 for(int k=0;k<l;k++) 12 if(s[k]==' ') ss+="00000"; 13 else ss+=q.substr(5*(s[k]-'A'),5); 14 while(t<5*l) 15 { 16 c++;x=c;y=c; 17 while(y+c<=m+1&&t<5*l){a[x][y]=ss[++t-1]-'0';y++;}y--;x++; 18 while(x+c<=n+1&&t<5*l){a[x][y]=ss[++t-1]-'0';x++;}x--;y--; 19 while(y>=c&&t<5*l){a[x][y]=ss[++t-1]-'0';y--;}y++;x--; 20 while(x>c&&t<5*l){a[x][y]=ss[++t-1]-'0';x--;} 21 } 22 for(int i=1;i<=n;i++) 23 for(int j=1;j<=m;j++) 24 cout<<a[i][j]; 25 return 0; 26 }



