CF1466 E. Apollo versus Pan

 Problem - 1466E - Codeforces

 

题意：

给出一个序列X，求

 

 

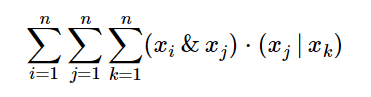
前后两项都有xj，那我们就枚举xj

设所有的数与xj按位与的和为sa

所有的数与xj按位或的和为sb

那么枚举的xj对答案的贡献是sa*sb

按位与的和sa怎么求？

按二进制位考虑，对于xj来说，如果它的第k位二进制为1

这一位1可以与所有的第k位为1的数按位与产生贡献

所以若n个数第k位为1的有cnt个，那么xj的这一位的贡献就是cnt * 2^k

按位或的和sb怎么求？

它等于n个数的和+n倍的xj - sa

就是类似于容斥原理

 

 

#include<bits/stdc++.h>
 
using namespace std;
 
const int mod=1e9+7;
 
#define N 500002
 
long long a[N];
 
long long bit[61]; 
int sum[61];
 
int main()
{
    int T,n;
    long long s1,s2,ans,tot;
    bit[0]=1;
    for(int i=1;i<60;++i) bit[i]=bit[i-1]<<1;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        tot=0;
        memset(sum,0,sizeof(sum));
        for(int i=1;i<=n;++i) 
        {
            scanf("%lld",&a[i]);
            for(int j=0;j<60;++j) 
                if(bit[j]&a[i]) ++sum[j];
            tot=(tot+a[i])%mod;
        }
        ans=0;
        for(int i=1;i<=n;++i)
        {
            s1=s2=0;
            for(int j=0;j<60;++j)
                if(bit[j]&a[i]) s1=(s1+bit[j]%mod*sum[j]%mod)%mod;
            s2=(tot+a[i]%mod*n%mod-s1+mod)%mod;
    //        printf("%lld %lld\n",s1,s2); 
            ans=(ans+s1*s2)%mod;
        }
        printf("%lld\n",ans);
    }
}