牛客练习赛78 F CCA的序列（矩阵乘法优化递推)

https://ac.nowcoder.com/acm/contest/11168/F

 

先考虑如何求给出的n个数有多少个不同的子序列

用f[i]表示以i为最后一个数字的子序列的个数

f[i]= 1 + ∑ f[j]  (1<=j<=k)

意为在之前求出的所有子序列最后加上x，都可以构成一个新的>1的子序列

加1 是i自己构成一个子序列

 

这个可以用一个变量sum记录Σ f[i] 1<=i<=k

每次更新f[i]的时候，在sum里面减去原来的f[i]，加上新的f[i]

最后的答案= ∑ f[i] 

 

然后考虑往后面加m个数

如果加的数是x，会把 f[x]更改为 1 + ∑ f[i] 

那么一定是加f[x]最小的x

根据式子可以发现，f[i]是递增的

所以最后出现时间越靠前的x，f[x]越小

按最后出现时间把f[x]从小到大排序

为什么不能直接按f[x] ? 因为f[x]取模了。。。

 

如果用g(i)表示  最后出现时间为第i小，并且以它为子序列最后一个数的子序列个数

假设k=4

可以得到矩阵转移式子如下：

 

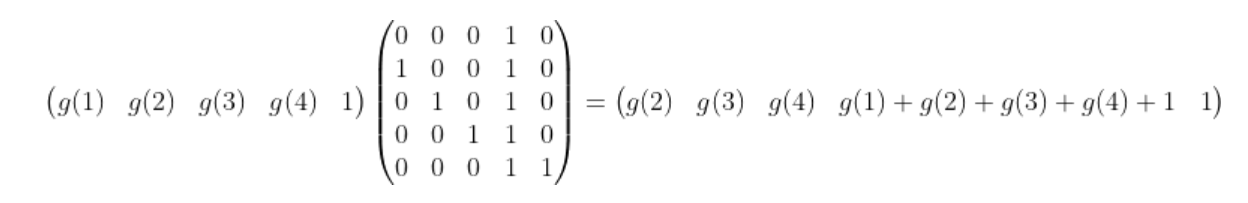
 用矩阵乘法加速即可

 

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;

int k;
int f[111];

const int mod=1e9+7;

int a[111][111];
int g1[111],g2[111][111];

struct node
{
    int pos,tot;
}e[111];

void mul(int x[111],int y[111][111])
{
    memset(g1,0,sizeof(g1));
    for(int i=1;i<=k+1;++i)
        for(int j=1;j<=k+1;++j)
            g1[i]=(g1[i]+1ll*x[j]*y[j][i]%mod)%mod;
    memcpy(f,g1,sizeof(f));
}

void mul(int x[111][111],int y[111][111])
{
    memset(g2,0,sizeof(g2));
    for(int i=1;i<=k+1;++i)
        for(int j=1;j<=k+1;++j)
            for(int l=1;l<=k+1;++l)
                g2[i][j]=(g2[i][j]+1ll*x[i][l]*y[l][j]%mod)%mod;
    memcpy(a,g2,sizeof(a)); 
}

bool cmp(node p,node q)
{
    return p.pos<q.pos;
}

int main()
{
    int n,x,sum=0,t;
    long long m;
    scanf("%d%lld%d",&n,&m,&k);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&x);
        t=e[x].tot;
        e[x].tot=sum+1;
        e[x].pos=i;
        sum=(sum-t+mod)%mod;
        sum=(sum+e[x].tot)%mod;
    }
    sort(e+1,e+k+1,cmp); 
    for(int i=1;i<=k;++i) f[i]=e[i].tot;
    f[k+1]=1;
    for(int i=1;i<k;++i) a[i+1][i]=1; 
    for(int i=1;i<=k+1;++i) a[i][k]=1;
    a[k+1][k+1]=1;
    while(m)
    {
        if(m&1) mul(f,a);
        mul(a,a);
        m>>=1;
    }
    int ans=0;
    for(int i=1;i<=k;++i) ans=(ans+f[i])%mod;
    printf("%d",ans);
}