天梯赛 迎风一刀斩

https://pintia.cn/problem-sets/994805046380707840/problems/994805051631976448

 

一、除了水平或竖直切一刀，两个图形各有1条边不平行于坐标轴

二、切出的两个图形仅有以下几种可能：

三角形+三角形、三角形+直角梯形、三角形+五边形、直角梯形+直角梯形、矩形+矩形

1、三角形+三角形

判断2个三角形是否全等即可，判断全等用SSS更容易

2、三角形+梯形

判断三角形 和 将梯形补成矩形缺的那块三角形 是否全等即可

3、三角形+五边形

判断三角形 和 将五边形补成矩形缺的那块三角形 是否全等

但是寻找缺的那块三角形时，用的平行于坐标轴的边相减，得到缺的直角三角形边长

但是有4条边平行于坐标轴的五边形不一定是缺了三角形，比如下面左图

                  

 

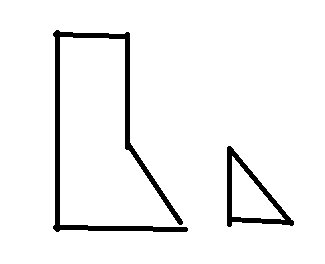
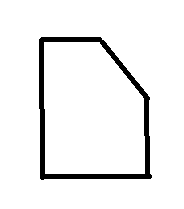
 符合要求的是右图

这两种五边形的区别是：

从不平行于坐标轴的那条边开始，

左图 依次遇到的是 相互平行边中的长边、长边、短边、短边，或者是短短长长

右图 依次遇到的是 相互平行边中的短边、长边、长边、短边

4、直角梯形+直角梯形

判断高相等，以及 图形A上底+图形B下底=图形A下底+图形B上底

5、矩形+矩形

判断是否有一条边相等即可

 

#include<cstdio>
#include<algorithm>

using namespace std; 

struct node
{
    int x,y;
}e[11],f[11];

void cal(node *p,int m,int &x0,int &x1,int &y0,int &y1,int &s)
{
    int b,len;
    x0=x1=y0=y1=s=0;
    for(int i=0;i<m;++i)
    {
        b=(i+1)%m;
        if(p[i].x==p[b].x)
        {
            len=abs(p[i].y-p[b].y);
            if(len>x1) x0=x1,x1=len;
            else x0=len;
            s++;
        }
        else if(p[i].y==p[b].y)
        {
            len=abs(p[i].x-p[b].x);
            if(len>y1) y0=y1,y1=len;
            else y0=len;
            s++;
        }
    }
}

bool judge()
{
    int b,tmp[5],k,a;
    for(int i=0;i<5;++i)
    {
        b=(i+1)%5;
        if(f[i].x==f[b].x) tmp[i]=abs(f[i].y-f[b].y);
        else if(f[i].y==f[b].y) tmp[i]=abs(f[i].x-f[b].x);
        else k=i;
    }
    if(tmp[(k+1)%5]>tmp[(k+3)%5]) a=1;
    else a=-1;
    if(tmp[(k+2)%5]>tmp[(k+4)%5]) b=1;
    else b=-1;
    return a*b<0;
}

bool solve(int m1,int m2)
{
    int x0,x1,y0,y1,X0,Y0,X1,Y1;
    int xa,ya,xb,yb,sa,sb;
    cal(e,m1,x0,x1,y0,y1,sa);
    xa=x1-x0;
    ya=y1-y0;
    cal(f,m2,X0,X1,Y0,Y1,sb);
    xb=X1-X0;
    yb=Y1-Y0;
    if(m1==4 && m2==4) 
    {
        if(sa==4 && sb==4) return x0==X0 || x0==Y0 || y0==X0 || y0==Y0;
        if(sa!=m1-1 || sb!=m2-1) return false;
        int h0,h1,kx0,kx1,kd0,kd1;
        if(!x0) h0=x1,kx0=y0,kd0=y1;
        else h0=y1,kx0=x0,kd0=x1;
        if(!X0) h1=X1,kx1=Y0,kd1=Y1;
        else h1=Y1,kx1=X0,kd1=X1;
        if(h0!=h1 || kx0+kd1!=kd0+kx1) return false;
        if(xa==xb && ya==yb) return true;
        if(xa==yb && ya==xb) return true;
        return false;
    }
    else
    {
        if(sa!=m1-1 || sb!=m2-1 || sa>4 || sb>4) return false;
        if(m1==4 && m2!=4) return false; 
        if(m2==5)
            if((xa==xb && ya==yb)||(xa==yb && ya==xb)) return judge();
            else return false;
        else
        {
            if(xa==xb && ya==yb) return true;
            if(xa==yb && ya==xb) return true;
            return false;
    
        }
    }
}

int main()
{
    int T,m1,m2;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&m1);
        for(int i=0;i<m1;++i) scanf("%d%d",&e[i].x,&e[i].y);
        scanf("%d",&m2);
        for(int i=0;i<m2;++i) scanf("%d%d",&f[i].x,&f[i].y);
        if(m1>m2) swap(m1,m2),swap(e,f);
        puts(solve(m1,m2) ? "YES" : "NO");
    }
    return 0;
} 

 

L3-006 迎风一刀斩 (30分)

 

迎着一面矩形的大旗一刀斩下，如果你的刀够快的话，这笔直一刀可以切出两块多边形的残片。反过来说，如果有人拿着两块残片来吹牛，说这是自己迎风一刀斩落的，你能检查一下这是不是真的吗？

注意摆在你面前的两个多边形可不一定是端端正正摆好的，它们可能被平移、被旋转（逆时针90度、180度、或270度），或者被（镜像）翻面。

这里假设原始大旗的四边都与坐标轴是平行的。

输入格式：

输入第一行给出一个正整数N（≤20），随后给出N对多边形。每个多边形按下列格式给出：

kx​1​​y​1​​⋯x​k​​y​k​​

其中k（2<k≤10）是多边形顶点个数；(x​i​​,y​i​​)（0≤x​i​​,y​i​​≤10​8​​）是顶点坐标，按照顺时针或逆时针的顺序给出。

注意：题目保证没有多余顶点。即每个多边形的顶点都是不重复的，任意3个相邻顶点不共线。

输出格式：

对每一对多边形，输出YES或者NO。

输入样例：

8
3 0 0 1 0 1 1
3 0 0 1 1 0 1
3 0 0 1 0 1 1
3 0 0 1 1 0 2
4 0 4 1 4 1 0 0 0
4 4 0 4 1 0 1 0 0
3 0 0 1 1 0 1
4 2 3 1 4 1 7 2 7
5 10 10 10 12 12 12 14 11 14 10
3 28 35 29 35 29 37
3 7 9 8 11 8 9
5 87 26 92 26 92 23 90 22 87 22
5 0 0 2 0 1 1 1 2 0 2
4 0 0 1 1 2 1 2 0
4 0 0 0 1 1 1 2 0
4 0 0 0 1 1 1 2 0

 

输出样例：

YES
NO
YES
YES
YES
YES
NO
YES