hdu 3511 Prison Break

http://acm.hdu.edu.cn/showproblem.php?pid=3511

 

题意：

给出n个相离或包含的圆，问最里层的圆是第几层

 

竖着的扫描线与圆在最左侧相切时

1、线在圆的上方或下方无交点，则该圆在第1层

2、线在圆的上下方都有交点，且上下方的交点属于同一个圆C，则该圆在圆C的里面一层

3、线在圆的上下方都有交点，上方交于圆E，下方交于圆F，EF其中一个在另一个里面，则该圆与在里面的那个圆处在同一层

4、线在圆的上下方都有交点，上方交于圆E，下方交于圆F，EF在同一层，则该圆与EF在同一层

 

扫描线从左往右扫，用set维护当前扫描线与圆的交点的纵坐标，set在线修改排序规则（这波操作绝了）

每次取出圆上下的交点，计算圆的层次

一个圆往set里加两次，一次用于计算靠上的交点 一次用于计算靠下的交点 ，

往set里加的时候，这个圆与扫描线相切，交点纵坐标是一样的，如果set按交点坐标从大到小排序，必须先加那个用于靠上的交点的，以维持set里交点相对位置的正确。

 

set在线修改排序规则应该不能保证所有数据在新规则下有序，不过插入点的前一个和后一个好像是正确的

 

 

#include<set>
#include<cmath>
#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

#define N 50001

int line;

struct Line
{
    int id,xi;
}e[N<<1];

int lev[N];

bool equal(double a,double b)
{
    return abs(a-b)<1e-7;
}

struct Circle
{
    int x,y,r;
    
    double gety(int f)
    {
        double dy=sqrt(1.0*r*r-1.0*(line-x)*(line-x));
        return y+dy*f;
    }
        
}cir[N];

struct Node
{
    int id,tag;
    
    Node(){}
    Node(int id_,int tag_) : id(id_),tag(tag_) {}
    
    bool operator < (const Node p) const
    {
        double ya=cir[id].gety(tag),yb=cir[p.id].gety(p.tag);
        if(!equal(ya,yb)) return ya>yb;
        return tag>p.tag;
    }

};

set<Node>s; 

bool cmp(Line p,Line q)
{
    return p.xi<q.xi;
}

int main()
{
    int n,m,k,ld,rd,ans;
    set<Node>:: iterator l,r;
    while(scanf("%d",&n)!=EOF)
    {
        m=0;
        for(int i=0;i<n;++i) 
        {
             scanf("%d%d%d",&cir[i].x,&cir[i].y,&cir[i].r);
             e[++m].id=i;
             e[m].xi=cir[i].x-cir[i].r;
            e[++m].id=i+n;
            e[m].xi=cir[i].x+cir[i].r;
        }
        sort(e+1,e+m+1,cmp);
        for(int i=1;i<=m;++i)
        {
            k=e[i].id%n;
            line=e[i].xi;
            if(e[i].id<n)
            {
                s.insert(Node(k,1));
                l=s.lower_bound(Node(k,1));
                r=l;
                r++;
                if(l==s.begin() || r==s.end()) lev[e[i].id]=1;
                else
                {
                    l--;
                    ld=(*l).id;
                    rd=(*r).id;
                    if(ld==rd) lev[e[i].id]=lev[ld]+1;
                    else lev[e[i].id]=max(lev[ld],lev[rd]);
                }
                s.insert(Node(k,-1));
            }
            else
            {
                s.erase(Node(k,1));
                s.erase(Node(k,-1));
            }
        }
        ans=0;
        for(int i=0;i<n;++i) ans=max(ans,lev[i]);
        printf("%d\n",ans);
    }
    return 0;
}    

 

 

Prison Break

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2206    Accepted Submission(s): 714

Problem Description

To save Sara, Michael Scofield was captured by evil policemen and he was arrested in Prison again. As is known to all, nothing can stop Michael, so Prison Break continues.
The prison consists of many circular walls. These walls won't intersect or tangent to each other.



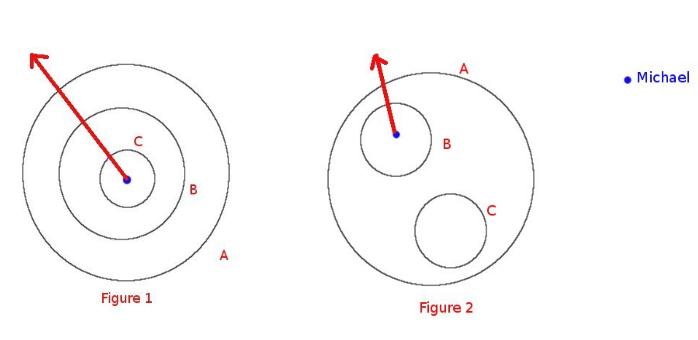
Now Michael is arrested in one of the deepest rooms, and he wants to know how many walls he has to break at least for running out. In figure 1, Michael has to break 3 walls at least and in figure 2, 2 walls are needed.

 

 

Input

There will be multiple test cases (no more than 10) in a test data.
For each test case, the first line contains one number: n (1<=n<=50,000) indicating the total number of circular walls.
Then n lines follow, each line contains three integers x, y, r. (x,y) indicates the center of circular wall and r indicates the radius of the wall.
-100,000<=x,y<=100,000
1 <= r <= 100,000
The input ends up with EOF.

 

 

Output

The least number of walls to break for running out.

 

 

Sample Input

3 0 0 1 0 0 2 0 0 3 3 0 0 10 5 0 1 -5 0 1

 

 

Sample Output

3 2

 

 

Source

2010 ACM-ICPC Multi-University Training Contest（8）——Host by ECNU