poj 2411 Mondriaan's Dream

http://poj.org/problem?id=2411

 

题意：

用1*2骨牌完美覆盖n*m棋盘，求方案数

 

将列的状态压缩，

一个骨牌有三种摆放方式

1表示骨牌竖着放且骨牌的上端在这一列，即这一列向下凸出

0表示骨牌竖着放且骨牌的下端在这一列，即这一列被上一列的一个竖着的骨牌覆盖，或者是骨牌横着覆盖

为什么这样表示

因为如果按行进行dp，只有状态1的覆盖方式对下一行的状态有要求

 

行与行之间的转移：

考虑状态1，相邻两行的同一列不能同时为1

考虑状态0，除了被上一行的1占的位置和本行的1占的位置，剩下的连续的0都是偶数个

所以

dp[i][j]=Σdp[i-1][k] （j&k==0 && j|k连续的0都是偶数个）

 

#include<cstdio>
#include<cstring>

using namespace std;

bool tag[2048];
int bit[12],len,con;

long long dp[12][2048]; 

bool pre(int x,int m)
{
     len=0;
     while(x) bit[++len]=x&1,x>>=1;
     for(int i=len+1;i<=m;++i) bit[i]=0;
     con=0;
     for(int i=1;i<=m;++i)
         if(bit[i]) 
             if(con&1) return false;
             else con=0;
         else con++;
     return !(con&1);
}

int main()
{
    int n,m,t;
    long long ans;
    while(1)
    {
        scanf("%d%d",&n,&m);
        for(int i=0;i<2048;++i) tag[i]=pre(i,m); 
        if((n&1) && (m&1)) 
        {
            printf("0\n");
            continue;
        }
        if(!n) return 0;
        memset(dp,0,sizeof(dp));
        dp[0][0]=1;
        t=(1<<m)-1;
        for(int i=1;i<=n;++i)
             for(int j=0;j<=t;++j)
                 for(int k=0;k<=t;++k)
                     if(!(j&k) && tag[j|k])
                         dp[i][j]+=dp[i-1][k];
        printf("%lld\n",dp[n][0]);
    }
}

 

Mondriaan's Dream

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 24293		Accepted: 13446

Description

Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

Output

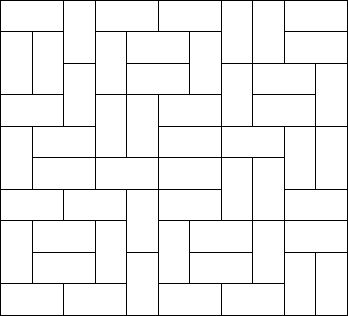For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

Sample Output

1
0
1
2
3
5
144
51205

Source

Ulm Local 2000