线段树——讲课用——扫描线

扫描线求矩形并

扫描线是一根假想的线，按照一个特定方向扫过一个二维平面，在扫描过程中完成相关信息的计算

矩形并的面积=Σ 一条线覆盖的矩形长度*这条线的宽度

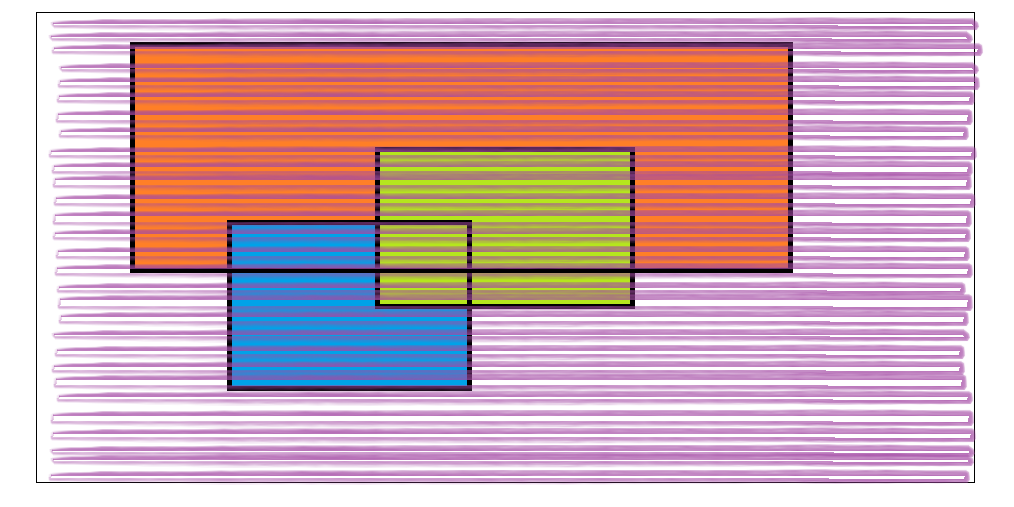
线的宽度呢？

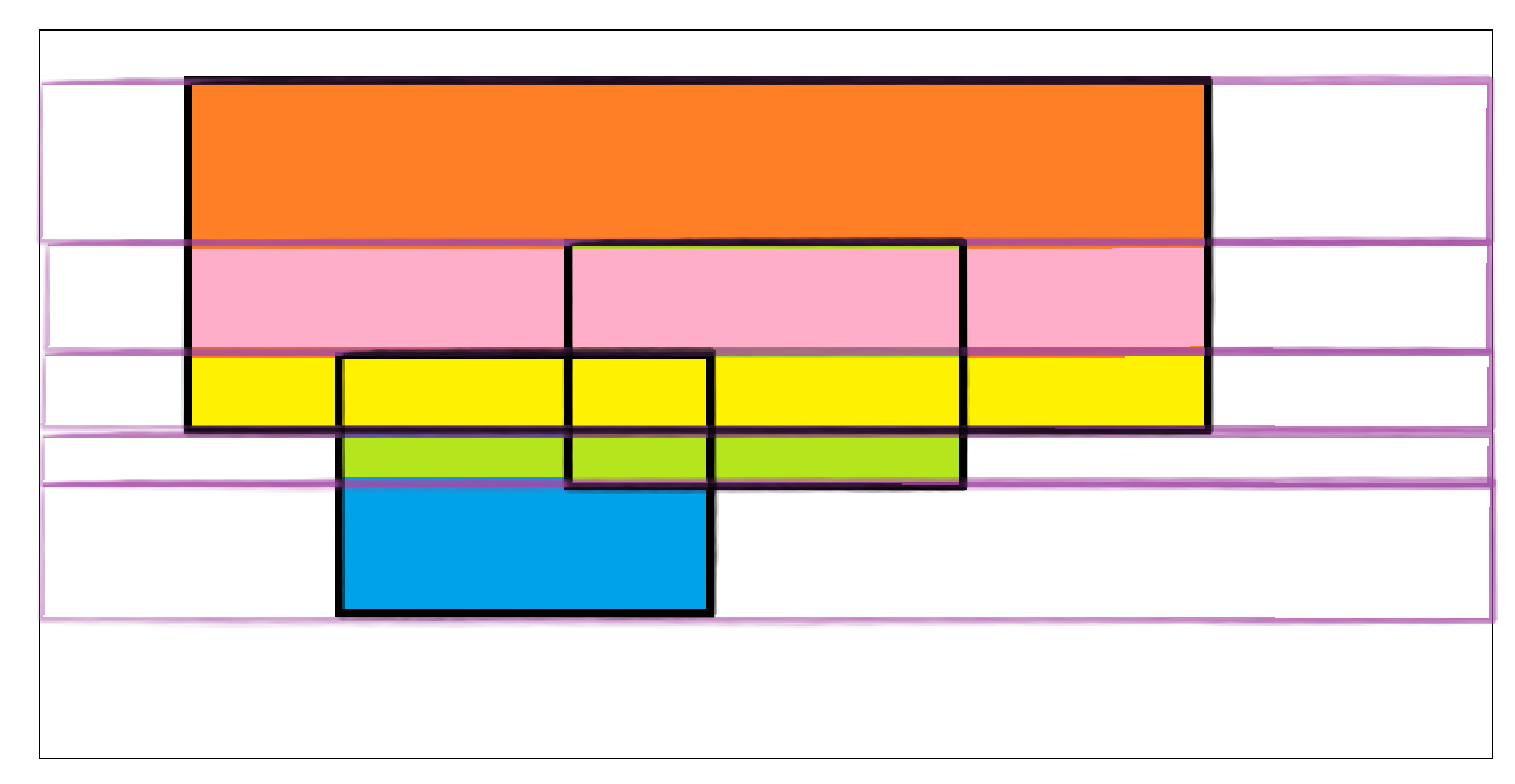
倘若线太细，当线在最下面蓝色区域扫时，它所覆盖的矩形长度不变

倘若线太粗，一条线覆盖的矩形宽度不一致，不能直接相加

所以扫描线在扫描过程中宽度随时调整，上图最终用5条线扫过

 

现在假设有一条线，从下往上扫过整个图形，用线段树维护现在这条线所覆盖的矩形长度

扫到矩形的下边，就往线段树里压入一条线

扫到矩形的上边，就从线段树里退出一条线

如何实现此过程？

用 col表示线段树上节点覆盖的线段条数

用f标记矩形的上下边，下边为1，上边为-1

那么col+=f 即可实现这一过程

当col>0时，表示扫描线上这块区域有矩形覆盖

当col=0时，表示扫描线上这块区域无矩形覆盖

 

所以，

如果扫描线是从下往上或从上往下扫，那就需要将矩形的横边按顺序排列，线段树里维护水平扫描线扫过的长度

如果扫描线是从左往右或从右往左扫，那就需要将矩形的竖边按顺序排列，线段树里维护竖直扫描线扫过的长度

 

矩形个数少，矩形的坐标可能是小数，也可能非常大

所以线段树叶节点不能表示单位长度为1的扫描线

将数据离散化即可

用sum表示扫描线覆盖矩形的实际长度

那么每一条扫描线扫描完毕后，答案累加 实际长度*线的宽度

线的宽度即为相邻两矩形边的坐标之差

 

小细节：

倘若矩形一条边离散化后对应区间为[1,5]，那么线段树中实际操作的区间应为[1,4]

因为线段树的叶节点是点，实际代表的区间是[L,L+1]

 

题目链接：http://codevs.cn/problem/3044/

#include<cstdio>
#include<iostream> 
#include<algorithm>

using namespace std;

#define N 101 

struct node
{
    double y1,y2,x;
    int f;
    bool operator < (node a) const
    {
        return x<a.x;
    }
}e[N<<1];

double hash[N<<1]; 

int opl,opr,fl; 

double sum[N<<3];
int col[N<<3];

void up(int k,int l,int r)
{
    if(col[k]) sum[k]=hash[r+1]-hash[l];
    else if(l==r) { sum[k]=0; return; }
    else sum[k]=sum[k<<1]+sum[k<<1|1];
}

void change(int k,int l,int r)
{
    if(l>=opl && r<=opr)
    {
        col[k]+=fl;
        up(k,l,r);
        return;
    }
    int mid=l+r>>1;
    if(opl<=mid) change(k<<1,l,mid);
    if(opr>mid) change(k<<1|1,mid+1,r);
    up(k,l,r);
}

int main()
{
    int n,m;
    double x1,y1,x2,y2;
    double ans;
    while(1)
    {
        scanf("%d",&n);
        if(!n) return 0;
        for(int i=1;i<=n;++i)
        {
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            e[i*2-1].x=x1; e[i*2-1].f=1; 
            e[i*2-1].y1=y1; e[i*2-1].y2=y2;
            e[i*2].x=x2; e[i*2].f=-1; 
            e[i*2].y1=y1; e[i*2].y2=y2;
            hash[i*2-1]=y1; hash[i*2]=y2;
        }
        sort(hash+1,hash+2*n+1);
        sort(e+1,e+2*n+1);
        m=n<<1; 
        ans=0;
        for(int i=1;i<=m;++i)
        {
            opl=lower_bound(hash+1,hash+m+1,e[i].y1)-hash;
            opr=lower_bound(hash+1,hash+m+1,e[i].y2)-hash-1;
            fl=e[i].f;
            change(1,1,m);
            ans+=sum[1]*(e[i+1].x-e[i].x); 
        }
        printf("%.2lf\n",ans);
    }
}