Codeforces Round #469 Div. 2题解
You are at a water bowling training. There are l people who play with their left hand, r people, who play with their right hand, and aambidexters, who can play with left or right hand.
The coach decided to form a team of even number of players, exactly half of the players should play with their right hand, and exactly half of the players should play with their left hand. One player should use only on of his hands.
Ambidexters play as well with their right hand as with their left hand. In the team, an ambidexter can play with their left hand, or with their right hand.
Please find the maximum possible size of the team, where equal number of players use their left and right hands, respectively.
The only line contains three integers l, r and a (0 ≤ l, r, a ≤ 100) — the number of left-handers, the number of right-handers and the number of ambidexters at the training.
Print a single even integer — the maximum number of players in the team. It is possible that the team can only have zero number of players.
1 4 2
6
5 5 5
14
0 2 0
0
In the first example you can form a team of 6 players. You should take the only left-hander and two ambidexters to play with left hand, and three right-handers to play with right hand. The only person left can't be taken into the team.
In the second example you can form a team of 14 people. You have to take all five left-handers, all five right-handers, two ambidexters to play with left hand and two ambidexters to play with right hand.
题意：有一些保龄球球员，其中一些惯用左手，另一些惯用右手，还有一些两手混用，现在需要使得用左手的球员和用右手的球员两两配对参加比赛，问最多能选择多少个球员参加比赛。
题解：我们贪心的考虑，让两种球员的数量尽可能相等，直接从两手混用的球员里取出尽可能少的球员放到人数较少的那一堆人里，然后最终的答案就是惯用左手的球员和惯用右手的球员的数量之间取个min，乘以2，然后加上两手混用的人数/2下取整（剩下的一拨人分别让他们惯用左手和右手）的值。
题意：一个人截获了一些归档，每个归档有若干个文件，归档中的每个文件是分成若干块传输的。传输后文件的顺序保持不变。如果两个归档的长度相等，这个人就认为这两个归档是同一归档。现在给定两个长度相等的归档和其中每一块的大小，问最多可以把每一个归档划分为多少个文件。
题解：我们贪心的想，对每个归档都做一个前缀和处理，对于我们只需要找出两个前缀和中相同数字的个数就行了，判断的时候不能$O(n^2)$枚举，因为归档的传递是严格从右到左的，所以如果两个文件大小不相等就让较小的前缀和指针后移一个块，如果两个文件大小相等就都后移一个块，答案++，同时把两个文件大小置0.
Oleg writes down the history of the days he lived. For each day he decides if it was good or bad. Oleg calls a non-empty sequence of days a zebra, if it starts with a bad day, ends with a bad day, and good and bad days are alternating in it. Let us denote bad days as 0and good days as 1. Then, for example, sequences of days 0, 010, 01010 are zebras, while sequences 1, 0110, 0101 are not.
Oleg tells you the story of days he lived in chronological order in form of string consisting of 0 and 1. Now you are interested if it is possible to divide Oleg's life history into several subsequences, each of which is a zebra, and the way it can be done. Each day must belong to exactly one of the subsequences. For each of the subsequences, days forming it must be ordered chronologically. Note that subsequence does not have to be a group of consecutive days.
In the only line of input data there is a non-empty string s consisting of characters 0 and 1, which describes the history of Oleg's life. Its length (denoted as |s|) does not exceed 200 000 characters.
If there is a way to divide history into zebra subsequences, in the first line of output you should print an integer k (1 ≤ k ≤ |s|), the resulting number of subsequences. In the i-th of following k lines first print the integer li (1 ≤ li ≤ |s|), which is the length of the i-th subsequence, and then li indices of days forming the subsequence. Indices must follow in ascending order. Days are numbered starting from 1. Each index from 1 to n must belong to exactly one subsequence. If there is no way to divide day history into zebra subsequences, print -1.
Subsequences may be printed in any order. If there are several solutions, you may print any of them. You do not have to minimize nor maximize the value of k.
0010100
3
3 1 3 4
3 2 5 6
1 7
111
-1
题意：给定一个01串，规定形如$01\underbrace{01\cdots01}_{n个}0$的串为斑马串。将给定的01串划分为若干个斑马串，从给定的01串中找若干个子序列，使得每个子序列都是斑马串，问有多少个斑马串，并输出每个斑马串的位置。
题解：贪心的分配01串的每一个字符。把字符串分为斑马串和接近斑马串（以0开头且以1结尾），如果当前字符是个0就加入到接近斑马串中的任意一个，使其变成一个斑马串，如果此时没有接近斑马串就不可能构造出符合题意的斑马串；如果当前字符是1就加入到斑马串中的任意一个，使其变成一个接近斑马串，和前一种情况类似的，如果此时没有斑马串就不可能构造出符合题意的斑马串。如果最后没有接近斑马串的存在，就输出解，否则输出-1.
Dima is a beginner programmer. During his working process, he regularly has to repeat the following operation again and again: to remove every second element from the array. One day he has been bored with easy solutions of this problem, and he has come up with the following extravagant algorithm.
Let's consider that initially array contains n numbers from 1 to n and the number i is located in the cell with the index 2i - 1 (Indices are numbered starting from one) and other cells of the array are empty. Each step Dima selects a non-empty array cell with the maximum index and moves the number written in it to the nearest empty cell to the left of the selected one. The process continues until all nnumbers will appear in the first n cells of the array. For example if n = 4, the array is changing as follows:
You have to write a program that allows you to determine what number will be in the cell with index x (1 ≤ x ≤ n) after Dima's algorithm finishes.
The first line contains two integers n and q (1 ≤ n ≤ 1018, 1 ≤ q ≤ 200 000), the number of elements in the array and the number of queries for which it is needed to find the answer.
Next q lines contain integers xi (1 ≤ xi ≤ n), the indices of cells for which it is necessary to output their content after Dima's algorithm finishes.
For each of q queries output one integer number, the value that will appear in the corresponding array cell after Dima's algorithm finishes.
4 3
2
3
4
3
2
4
13 4
10
5
4
8
13
3
8
9
The first example is shown in the picture.
In the second example the final array is [1, 12, 2, 8, 3, 11, 4, 9, 5, 13, 6, 10, 7].
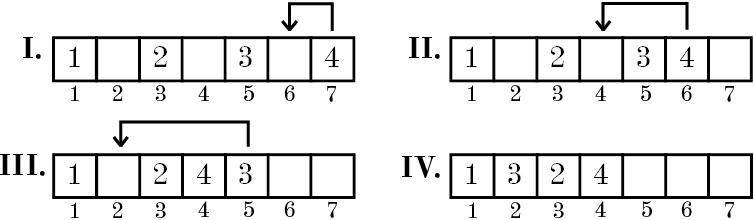
题意：给你一个数组，数组中隔一个格子有一个数，每次跳跃都是将最大的数跳到离它最近的右边一个格子里，有Q次询问，每次询问跳跃完后某个格子里是什么数。
题解：我们假设初始数组长度为$n$，通过打表找规律我们发现，改变后的数组里，下标为奇数的元素的值为$\left\frac{n+1}{2}\rfloor$。
证明：
很容易发现，对于整个初始数组中前$\left\lceil\frac{n}{2}\right\rceil$个元素来说，它们并没有参与移动。对于初始数组中后$\left\lfloor\frac{n}{2}\right\rfloor$个元素来说，它们跳到的位置分两种情况讨论：
对于所有下标为奇数的元素，跳跃的路径上的元素下标一定是偶数，最终到达的元素下标也一定是偶数，也就是$\left\frac{n+1}{2}\rfloor$。
对于所有下标为偶数的元素，我们考虑移动到第$x$位的数，它在初始数组里的位置。我们知道，初始数组里下标为$i$的数为$\frac{i}{2}+1$，且这个数到达的第一个下标为奇数的位置就是它在初始数组中的位置。
最后移动到的的位置是$x$，那么在位置$x$之前有$\left\lfloor\frac{x}{2}\right\rfloor$个奇数位置存在一个数（显然区间$[1,x]$内有$\left\lfloor\frac{x}{2}\right\rfloor$个奇数，这些位置都是有一个数的），容易得到在它的右边有$n-\left\lfloor\frac{x}{2}\right\rfloor$个数（区间$[x+1,n]$中共有$n-\left\lfloor\frac{x}{2}\right\rfloor$个奇数），又因为每次跳跃的数一定是数组里面最右边的一个数，所以我们就得到了最后一次跳跃前这个数的位置$x'=x+\left(n-\left\lfloor\frac{x}{2}\right\rfloor\right)$，如果$x'$还是偶数，那么就继续跳跃，直到这个下标在初始数组中对应一个数为止。
题意：某公司建立了很多个数据中心，每份数据保存在两个数据中心中。每个数据中心在一天内都有一个小时需要维护，维护期间数据无法下载。现在公司想要将一些数据中心的维护时间推迟一个小时，以适应时区夏令时的变更，问最少选择多少个数据中心在同一时间进行维护。
题解：图论题。我们把必须在同一时间进行维护的两个数据中心之间连一条边，然后Tarjan求强连通分量即可。
即满足条件$(a[x]+1)\bmod h=a[y]$连一条$x\rightarrow y$的边，满足条件$(a[y]+1)\bmod h=a[x]$的连一条$y\rightarrow x$的边。
题意：有两个宿管查寝，第一个宿管从$1$号宿舍走到$n$号宿舍，第二个宿管从$n$号宿舍走到$1$号宿舍，并且如果$n$是奇数，则中间的宿舍只会被查一次，每个宿舍里都应该有$b$个学生，但是查寝时学生们不一定在他们应在的宿舍。如果所有宿舍都被查过了，则查寝结束。
查寝过程如下：宣布查寝开始，每个学生可以选择跑到距离自己目前所在宿舍不超过$d$的宿舍，每一个学生也可以选择藏在床底下（这样宿管就看不到他了），也可以选择留在原地。查寝开始，两个宿管分别清点所查宿舍的人数，如果人数不等于应有的人数，就记下来，这个宿舍就gg了，宿管离开宿舍时会把门锁上，没有人能够进出这个宿舍。
现在问采取若最优策略最少被记下多少次。
题解：假设只有一个宿管从左往右查寝，那就从左往右转移人员，如果人太多了就转移到下一个宿舍；如果人不够并且后面的宿舍能凑够人数就凑够人数；如果都不行的话所有学生都跑到下一间宿舍，如果是最后一间宿舍了，那多余的学生就藏在床底下。这样可以保证至少没有宿舍会多出一些人来。这样做需要保证学生走的路径不能交叉（一个学生$i$从$a$宿舍跑到$b$宿舍，另一个学生$j$从$b$宿舍跑到$a$宿舍，什么也没改变，就不是最优解了）。
然后我们只需要维护一个前缀和，表示能移动的学生个数，然后就能快速判断能不能把学生移动到其他宿舍了。
考虑原题给出的条件，类似的，我们将学生尽量向中间宿舍进行转移，这样如果一个宿舍人数不够并且其他宿舍转移不过去的话就放弃这个宿舍，这样下来可以保证至少不会有宿舍多出一些人，最后不行的就是那些无法转移过去的宿舍。
