Codeforces Round #468 Div. 2题解
A. Friends Meeting
Two friends are on the coordinate axis Ox in points with integer coordinates. One of them is in the point x1 = a, another one is in the point x2 = b.
Each of the friends can move by one along the line in any direction unlimited number of times. When a friend moves, the tiredness of a friend changes according to the following rules: the first move increases the tiredness by 1, the second move increases the tiredness by 2, the third — by 3 and so on. For example, if a friend moves first to the left, then to the right (returning to the same point), and then again to the left his tiredness becomes equal to 1 + 2 + 3 = 6.
The friends want to meet in a integer point. Determine the minimum total tiredness they should gain, if they meet in the same point.
The first line contains a single integer a (1 ≤ a ≤ 1000) — the initial position of the first friend.
The second line contains a single integer b (1 ≤ b ≤ 1000) — the initial position of the second friend.
It is guaranteed that a ≠ b.
Print the minimum possible total tiredness if the friends meet in the same point.
3
4
1
101
99
2
5
10
9
In the first example the first friend should move by one to the right (then the meeting happens at point 4), or the second friend should move by one to the left (then the meeting happens at point 3). In both cases, the total tiredness becomes 1.
In the second example the first friend should move by one to the left, and the second friend should move by one to the right. Then they meet in the point 100, and the total tiredness becomes 1 + 1 = 2.
In the third example one of the optimal ways is the following. The first friend should move three times to the right, and the second friend — two times to the left. Thus the friends meet in the point 8, and the total tiredness becomes 1 + 2 + 3 + 1 + 2 = 9.
题目大意：两个人在数轴上的两个不同点上，要走到同一个点上。一个人每走一步积累的疲劳值是这个人总共走的步数，求最小的疲劳值之和。
贪心的考虑。因为一个人走的步数越多，积累的疲劳值越多。所以我们只需要求出中点来，然后让这两个人走到中点即可，这样两人走的步数就是相等的。
对于两个人在负半轴且第二个人在第一个人左侧的情况，还是取区间的中点。
#include <cmath>
#include <cstdio>
using namespace std;
int main()
{
int s=0,x1,x2,l,q,p=0;
scanf("%d%d",&x1,&x2);
l=abs(x1-x2);
if (l%2!=0)p=1;
for (q=1; q<=l/2; q++)s+=q;
s*=2;
s+=q*p;
printf("%d\n",s);
return 0;
}
题目大意：有n支队伍，用编号排名，第一名与第二名比赛，第三名与第四名比赛，以此类推，一场比赛输了的一方退出比赛。给定两个队伍的编号，输出这两支队伍第一次相遇的比赛场次。
题解：首先我们可以确定，设每一轮比赛剩余$cnt$人，则在每一轮比赛之后，都有$\left\lfloor\frac{cnt}{2}\right\rfloor$人被淘汰，所以比赛轮数与$\log_2n$有关，我们直接模拟$\log_2n$次比赛即可。每次比赛中，两人之间的距离会降低到$\left\lfloor|\frac{a}{2}-\frac{b}{2}|\right\rfloor$，因为有$\left\lfloor|a-b|\right\rfloor$场比赛进行。我们并不需要知道在这$\log_2n$场比赛中，哪些人被淘汰了，只需要知道两个人在比赛中所处的相对排名即可。
#include <bits/stdc++.h>
using namespace std;
int rot,n,a,b;
int main()
{
scanf("%d%d%d",&n,&a,&b);
a+=(n-1);
b+=(n-1);
rot=log2(n);
for(int i=1;i<rot;i++)
{
a/=2;
b/=2;
if(a==b){printf("%d",i); return 0;}
}
printf("Final!");
return 0;
}
题目大意：构造一组数据，使得平均值等于给定的数据，并且使得相同的数字个数尽可能小。
思路：stO ljj Orz
如果最大-最小不是2，那么只能输出原序列
如果是2的话，要么把每2个次大的改成一个最小和一个最大，要么把一个最大和一个最小改成2个次大
两种情况取最优
贪心的正确性证明：
如果最大值-最小值为0，则序列中所有数都为同一个数，要想构造一个序列使得其平均值等于原序列，则构造出的序列一定与原序列相同。
如果最大值-最小值为1，则序列中所有数要么为最大值，要么为最小值，要想构造一个序列使得其平均值等于原序列，则构造出的序列一定与原序列相同。
如果最大值-最小值为2，那么序列中除最大值和最小值外，可能还有一个次大值，那么我们有两种修改方法：1.把一个最大值和一个最小值改为两个次大值，平均值不变；2.把两个次大值改为一个最大值和一个最小值，平均值也不变。明显的只要修改，那么就与原来的值不同，对答案没有贡献，只有需要保持不变的时候，才对答案有贡献，所以套用以上两个贪心的策略进行修改，使得尽可能多的值与原来的值不同即可。
In Arcady's garden there grows a peculiar apple-tree that fruits one time per year. Its peculiarity can be explained in following way: there are n inflorescences, numbered from 1 to n. Inflorescence number 1 is situated near base of tree and any other inflorescence with number i (i > 1) is situated at the top of branch, which bottom is pi-th inflorescence and pi < i.
Once tree starts fruiting, there appears exactly one apple in each inflorescence. The same moment as apples appear, they start to roll down along branches to the very base of tree. Each second all apples, except ones in first inflorescence simultaneously roll down one branch closer to tree base, e.g. apple in a-th inflorescence gets to pa-th inflorescence. Apples that end up in first inflorescence are gathered by Arcady in exactly the same moment. Second peculiarity of this tree is that once two apples are in same inflorescence they annihilate. This happens with each pair of apples, e.g. if there are 5 apples in same inflorescence in same time, only one will not be annihilated and if there are 8 apples, all apples will be annihilated. Thus, there can be no more than one apple in each inflorescence in each moment of time.
Help Arcady with counting number of apples he will be able to collect from first inflorescence during one harvest.
First line of input contains single integer number n (2 ≤ n ≤ 100 000) — number of inflorescences.
Second line of input contains sequence of n - 1 integer numbers p2, p3, ..., pn (1 ≤ pi < i), where pi is number of inflorescence into which the apple from i-th inflorescence rolls down.
Single line of output should contain one integer number: amount of apples that Arcady will be able to collect from first inflorescence during one harvest.
3
1 1
1
5
1 2 2 2
3
18
1 1 1 4 4 3 2 2 2 10 8 9 9 9 10 10 4
4
In first example Arcady will be able to collect only one apple, initially situated in 1st inflorescence. In next second apples from 2nd and 3rd inflorescences will roll down and annihilate, and Arcady won't be able to collect them.
In the second example Arcady will be able to collect 3 apples. First one is one initially situated in first inflorescence. In a second apple from 2nd inflorescence will roll down to 1st (Arcady will collect it) and apples from 3rd, 4th, 5th inflorescences will roll down to 2nd. Two of them will annihilate and one not annihilated will roll down from 2-nd inflorescence to 1st one in the next second and Arcady will collect it.
题目大意：给你一棵树，树上每个节点都有一个苹果。你在树根处，每一秒钟可以摘一个苹果，摘完苹果后，上一层的苹果会滚动到它的父亲结点，但是一个结点最多允许有一个苹果，如果一个结点的苹果个数为x，则在滚动后这个节点剩下$x\bmod 2$个苹果。问你能得到多少个苹果。
题解：将树分层，对于同一层，在下一秒内会滚动到父亲节点，由于一个节点最多有1个苹果，同时如果树上同一层有偶数个苹果则所有苹果都会消失，所以只需要做一遍DFS记录下每一层的苹果个数，答案就是有奇数个苹果的层数。
例如样例3，我们有树状图如下：
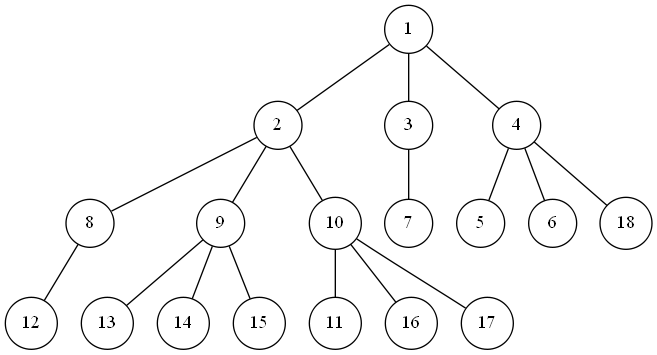
初始状态，在1处有一个苹果，collect掉
第一次滚动后，在1处有原来2,3,4的苹果，剩下1个，collect掉
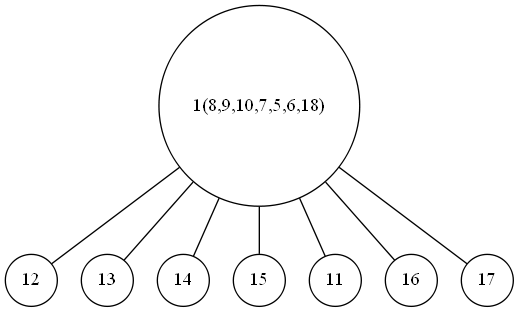
第二次滚动，在1处有原来8,9,10,7,5,6,18的苹果，剩下1个，collect掉
第三次滚动，在1处有原来12,13,14,15,11,16,17的苹果，剩下1个，collect掉
#include<cstdio>
using namespace std;
const int maxn=100000*2+10;
struct Edge{int u,v;}edge[maxn];
int head[maxn],cnt;
inline void add(int u,int v){edge[++cnt].u=head[u],edge[cnt].v=v,head[u]=cnt;}
int n,v,maxdep,ans;
int vis[maxn],depth[maxn];
void dfs(int pos,int dep)
{
if(dep>maxdep)maxdep=dep;
depth[dep]++;
for(int i=head[pos];i;i=edge[i].u)
{
int v=edge[i].v;
if(!vis[v])
{
vis[v]=1;
dfs(v,dep+1);
}
}
}
int main()
{
scanf("%d",&n);
for(int i=2;i<=n;i++)
{
scanf("%d",&v);
add(v,i);
}
dfs(1,1);
for(int i=1;i<=maxdep;i++)
if(depth[i]&1)++ans;
printf("%d\n",ans);
return 0;
}
Vasya and Kolya play a game with a string, using the following rules. Initially, Kolya creates a string s, consisting of small English letters, and uniformly at random chooses an integer k from a segment [0, len(s) - 1]. He tells Vasya this string s, and then shifts it k letters to the left, i. e. creates a new string t = sk + 1sk + 2... sns1s2... sk. Vasya does not know the integer k nor the string t, but he wants to guess the integer k. To do this, he asks Kolya to tell him the first letter of the new string, and then, after he sees it, open one more letter on some position, which Vasya can choose.
Vasya understands, that he can't guarantee that he will win, but he wants to know the probability of winning, if he plays optimally. He wants you to compute this probability.
Note that Vasya wants to know the value of k uniquely, it means, that if there are at least two cyclic shifts of s that fit the information Vasya knowns, Vasya loses. Of course, at any moment of the game Vasya wants to maximize the probability of his win.
The only string contains the string s of length l (3 ≤ l ≤ 5000), consisting of small English letters only.
Print the only number — the answer for the problem. You answer is considered correct, if its absolute or relative error does not exceed 10 - 6.
Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if 
technocup
1.000000000000000
tictictactac
0.333333333333333
bbaabaabbb
0.100000000000000
In the first example Vasya can always open the second letter after opening the first letter, and the cyclic shift is always determined uniquely.
In the second example if the first opened letter of t is "t" or "c", then Vasya can't guess the shift by opening only one other letter. On the other hand, if the first letter is "i" or "a", then he can open the fourth letter and determine the shift uniquely.
题目大意：给你一个字符串s，随机选取一段区间[0,k]，将这一段区间移动到剩下的字符串的左边，不知道t是什么，但是知道t的第一个字母，还能随便看t中的任意一个字母，问最优策略下获胜的概率是多少。
题解：概率题。固定起点为0，然后枚举不同字母开头，移动区间长度为[0,l-1]的结果。在枚举过程中记录不同的字符串种数和一个字符串的最大出现次数，最后计算概率即可。
题意：给定一个坐标轴，坐标轴上有很多条线段，保证一个整数点不被所有线段覆盖，最多询问k次，每次询问一个整数点上有多少条线段，问最多询问多少次（明显的答案小于等于k）才能知道这张图是不是满足给定的条件。
题解：读入时用差分数组维护线段，然后在O(n)的时间内把差分数组转为前缀和（数组中的每个元素表示每个点被覆盖的次数），然后做一遍最长上升子序列与最长下降子序列，则答案就是最长上升子序列和最长下降子序列的长度。
我们可以发现，在前缀和数组中如果遇到了下降的区间，则说明在下降的区间中有线段结束了。但是如果查询的时候不去查询那个线段，在这个不确定的地方形成了上升子序列，那么无法确定这个地方是新添了一条线段（有一条线段结束了），或者是原有的线段没有结束，所以任务就是确定不相交线段的条数。
至于怎么维护这个LIS的问题，直接$O(n\log n)$的方法，二分或者用树状数组/线段树查询区间$[1,i-1]$的区间最大值即可。
（如果英语水平比较高的话，直接看http://codeforces.com/blog/entry/58153?#comment-41833，这个评论给出了更加详细的解释。）
（终于知道什么叫做Confusing Problem了，highly misleading的题面qwq）
/*
So other people have been saying that they've seen this problem before, but I haven't, so I'll try to explain it as if you haven't seen it before either.
First thing's first, we notice that if a point is not in all segments, that is equivalent to saying that you can find two segments that are disjoint (draw a picture, you will see why this is true).
Next thing, we notice that if the number of segments decreases and then increases, there must be a pair of disjoint intervals (that is, Sasha is sure Teodor isn't lying). Let's look at sample test 2 to see what I mean. If you were to query the number of segments at each point going from left to right, you would get 1 2 2 1 2 2. Because at points 3, 4, and 5, the queries are 2, 1, and 2, that is, they go down and then up, so we know that there is some interval that ends at 3 and some other interval that starts at 5, so we have two disjoint intervals, and Sasha is sure there is a point that is not in all intervals. HOWEVER, if we were to only query points 1, 2, 3, 5, and 6, Sasha's knowledge of the above array would be 1 2 2 _ 2 2. If the blank was filled in with a 2, he still could not tell whether Teodor was lying. If you play around with the numbers more, you'll see that this is the case for any non-increasing sequence, non-decreasing sequence, and unimodal sequence. For example, other arrays like [1 _ _ 3 _ 5 6], [8 _ 2 2 _ 1], or [1 2 4 _ 6 _ _ 2 1] would not give Sasha enough information to tell whether Teodor is lying.
Thus, we can reformulate the question as follows: what is the longest unimodal subsequence of the array a, where a is the array such that ai is the number of intervals at index i.
This is easily solvable if you know $O(n\log n)$ LIS algorithm, since we just find LIS at each index, and LDS at each index, and test each possible point to be the peak, which will be linear, making the whole thing $O(n\log n)$. Also, constructing the array a is easily done in linear time, since we know all the segments in advance, so we can just increment left endpoints, decrement 1 past right endpoints, and calculate partial sums to get a.
*/
