Codeforces Round #467 Div.2题解

The recent All-Berland Olympiad in Informatics featured n participants with each scoring a certain amount of points.

As the head of the programming committee, you are to determine the set of participants to be awarded with diplomas with respect to the following criteria:

At least one participant should get a diploma.
None of those with score equal to zero should get awarded.
When someone is awarded, all participants with score not less than his score should also be awarded.

Determine the number of ways to choose a subset of participants that will receive the diplomas.

Input

The first line contains a single integer n (1 ≤ n ≤ 100) — the number of participants.

The next line contains a sequence of n integers a1, a2, ..., an (0 ≤ ai ≤ 600) — participants' scores.

It's guaranteed that at least one participant has non-zero score.

Output

Print a single integer — the desired number of ways.

Examples

input

Copy

4
1 3 3 2

output

input

Copy

3
1 1 1

output

input

Copy

4
42 0 0 42

output

Note

There are three ways to choose a subset in sample case one.

Only participants with 3 points will get diplomas.
Participants with 2 or 3 points will get diplomas.
Everyone will get a diploma!

The only option in sample case two is to award everyone.

Note that in sample case three participants with zero scores cannot get anything.

题目大意：给定$n$个人的成绩，如果一个人得了奖，则所有比他分数高得人都有奖励，得零分的人没有奖励，问有多少种发奖方案。

题解：这不是水题吗。就是统计一下给定数列中非零数的个数，顺便去个重就行了。

#include<cstdio>
#include<iostream>
using namespace std;
int n;
int num;
int ans=0;
bool vis[700];
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%d",&num);
        if(!num)continue;
        else if(vis[num])continue;
        else ans++,vis[num]=1; 
    }
    printf("%d\n",ans);
    return 0;
}

The weather is fine today and hence it's high time to climb the nearby pine and enjoy the landscape.

The pine's trunk includes several branches, located one above another and numbered from 2 to y. Some of them (more precise, from 2to p) are occupied by tiny vile grasshoppers which you're at war with. These grasshoppers are known for their awesome jumping skills: the grasshopper at branch x can jump to branches 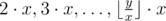$\text{[math]}$ .

Keeping this in mind, you wisely decided to choose such a branch that none of the grasshoppers could interrupt you. At the same time you wanna settle as high as possible since the view from up there is simply breathtaking.

In other words, your goal is to find the highest branch that cannot be reached by any of the grasshoppers or report that it's impossible.

Input

The only line contains two integers p and y ($2 ≤ p ≤ y ≤ 10^9$).

Output

Output the number of the highest suitable branch. If there are none, print -1 instead.

Examples

input

Copy

3 6

output

input

Copy

3 4

output

-1

Note

In the first sample case grasshopper from branch 2 reaches branches 2, 4 and 6 while branch 3 is initially settled by another grasshopper. Therefore the answer is 5.

It immediately follows that there are no valid branches in second sample case.

题意：给定有$y$个节点的一棵树，初始时在1号点有一只蝗虫，并且在$2,3,\ldots,p$的倍数的位置也有一只蝗虫，问没有蝗虫且编号最大的点的编号。如果所有点都被蝗虫占领输出-1.

题解：素数的变形。考虑一个事实，两素数隔的数的个数远远小于$10^9$，可以暴力判断是否为素数。所以我们可以从$y$开始，倒序枚举每一个点，暴力判断是否满足条件即可。事实上最多只需要枚举300个数就可以了，参考维基百科Prime Gap这个词条可以得知素数之间的间隔应该在$\log n$级别上。

比赛的时候一眼看出素数，开始往线性筛素数等方面考虑，然而线性筛会MLE+TLE，然后开始思考一些奇奇怪怪的方案。然后gg。

#include<cstdio>
#include<cstdlib>
using namespace std;
int p, y;
int ck(int n)
{
    for(int i = 2; i * i <= n && i <= p; i++)
        if(n % i == 0) return false;
    return true;
}
int main()
{
    scanf("%d%d",&p,&y);
    for(int i = y; i > p; i--)
        if(ck(i)) 
            printf("%d\n", i),exit(0);
    puts("-1");
    return 0;
}

Julia is going to cook a chicken in the kitchen of her dormitory. To save energy, the stove in the kitchen automatically turns off after k minutes after turning on.

During cooking, Julia goes to the kitchen every d minutes and turns on the stove if it is turned off. While the cooker is turned off, it stays warm. The stove switches on and off instantly.

It is known that the chicken needs t minutes to be cooked on the stove, if it is turned on, and 2t minutes, if it is turned off. You need to find out, how much time will Julia have to cook the chicken, if it is considered that the chicken is cooked evenly, with constant speed when the stove is turned on and at a constant speed when it is turned off.

Input

The single line contains three integers k, d and t (1 ≤ k, d, t ≤ 1018).

Output

Print a single number, the total time of cooking in minutes. The relative or absolute error must not exceed 10 - 9.

Namely, let's assume that your answer is x and the answer of the jury is y. The checker program will consider your answer correct if 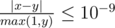$\text{[math]}$ .

Examples

input

Copy

3 2 6

output

6.5

input

Copy

4 2 20

output

20.0

Note

In the first example, the chicken will be cooked for 3 minutes on the turned on stove, after this it will be cooked for $\text{[math]}$ . Then the chicken will be cooked for one minute on a turned off stove, it will be cooked for $\text{[math]}$ . Thus, after four minutes the chicken will be cooked for $\text{[math]}$ . Before the fifth minute Julia will turn on the stove and after 2.5 minutes the chicken will be ready $\text{[math]}$ .

In the second example, when the stove is turned off, Julia will immediately turn it on, so the stove will always be turned on and the chicken will be cooked in 20 minutes.

题意：一个人要烤鸡，炉子每加热$k$分钟后就自动转到保温模式，直到这个人把它重新打开为止。加热状态下烤鸡需要$t$分钟，保温状态下烤鸡需要$2t$分钟。这个人每隔$d$分钟会去厨房看一次，转换到加热模式，问这个人多长时间以后才能吃到烤鸡。

题解：注意到有很多时间段是重复的，可以直接跳过。开始分类讨论：

如果$k\le d$，那么当这个人来的时候，炉子已经在保温状态了。这个人就会把炉子打开。从而继续加热$d$分钟。所以加热状态的时间段长度为$d$。

其他情况下，这个人每隔$p$分钟都会来一次开炉子。

计算一下周期，最后处理好不是完整周期的部分即可。

无需担心精度问题，因为每次都是除以二。

数学计算一下就行了。

#include<cstdio>
using namespace std;
typedef long long ll;
int main()
{
    ll k,d,t;
    scanf("%lld%lld%lld",&k,&d,&t);
    ll T = ((k-1)/d+1)*d;
    double ans = 0;
    double oneT = (T-k)*0.5+k;
    ans += ll(t/oneT)*T;
    ll ht = t/oneT;
    double st = t-ht*oneT;
    if(st < k)ans += st;
    else ans = ans+k+(st-k)*2;
    printf("%.1lf\n", ans);
    return 0;
}

Petya and Vasya arranged a game. The game runs by the following rules. Players have a directed graph consisting of n vertices and medges. One of the vertices contains a chip. Initially the chip is located at vertex s. Players take turns moving the chip along some edge of the graph. Petya goes first. Player who can't move the chip loses. If the game lasts for 106 turns the draw is announced.

Vasya was performing big laboratory work in "Spelling and parts of speech" at night before the game, so he fell asleep at the very beginning of the game. Petya decided to take the advantage of this situation and make both Petya's and Vasya's moves.

Your task is to help Petya find out if he can win the game or at least draw a tie.

Input

The first line of input contain two integers n and m — the number of vertices and the number of edges in the graph (2 ≤ n ≤ 105, 0 ≤ m ≤ 2·105).

The next n lines contain the information about edges of the graph. i-th line (1 ≤ i ≤ n) contains nonnegative integer ci — number of vertices such that there is an edge from i to these vertices and ci distinct integers ai, j — indices of these vertices (1 ≤ ai, j ≤ n, ai, j ≠ i).

It is guaranteed that the total sum of ci equals to m.

The next line contains index of vertex s — the initial position of the chip (1 ≤ s ≤ n).

Output

If Petya can win print «Win» in the first line. In the next line print numbers v1, v2, ..., vk (1 ≤ k ≤ 106) — the sequence of vertices Petya should visit for the winning. Vertex v1 should coincide with s. For i = 1... k - 1 there should be an edge from vi to vi + 1 in the graph. There must be no possible move from vertex vk. The sequence should be such that Petya wins the game.

If Petya can't win but can draw a tie, print «Draw» in the only line. Otherwise print «Lose».

Examples

input

Copy

output

Win
1 2 4 5

input

Copy

output

Lose

input

Copy

output

Draw

Note

In the first example the graph is the following:

$\text{[math]}$

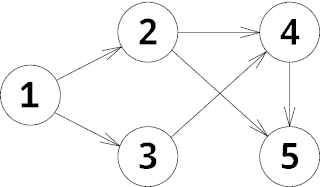
Initially the chip is located at vertex 1. In the first move Petya moves the chip to vertex 2, after that he moves it to vertex 4 for Vasya. After that he moves to vertex 5. Now it is Vasya's turn and there is no possible move, so Petya wins.

In the second example the graph is the following:

$\text{[math]}$

Initially the chip is located at vertex 2. The only possible Petya's move is to go to vertex 1. After that he has to go to 3 for Vasya. Now it's Petya's turn but he has no possible move, so Petya loses.

In the third example the graph is the following:

$\text{[math]}$

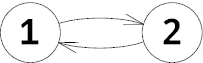
Petya can't win, but he can move along the cycle, so the players will draw a tie.

题意：在一个有向图上，两人移动一个物品，不能移动者输，但是后手睡着了，所以需要先手帮她完成这个比赛。先手想要赢得胜利，若能胜利输出方案，若先手一定输输出Lose，若游戏打平输出Draw。

题解：明显的，这道题的目的就是让后手走入死胡同，即要求一条终点为出度为0的点且经过偶数个点的路径。可以使用DFS来解决。

用DFS先对图进行黑白染色，起点设为黑色。如果能找到一个终点为白色的点，则说明能赢，输出方案。

否则再进行一次DFS，判断一个点能否变色（即到达一个点可能有很多不同路径，这些不同的路径经过的点的个数也有可能不同），如果终点可以变色就说明能赢，输出方案。

剩下的情况是不能获胜的方案。此时就需要在图中找一个环，明显的，如果在环中，先手一定有可走的点，即打平。用DFS判断一个点是否被多次访问即可，当然也能Tarjan判环。

Welcome to another task about breaking the code lock! Explorers Whitfield and Martin came across an unusual safe, inside of which, according to rumors, there are untold riches, among which one can find the solution of the problem of discrete logarithm!

Of course, there is a code lock is installed on the safe. The lock has a screen that displays a string of n lowercase Latin letters. Initially, the screen displays string s. Whitfield and Martin found out that the safe will open when string t will be displayed on the screen.

The string on the screen can be changed using the operation «shift x». In order to apply this operation, explorers choose an integer xfrom 0 to n inclusive. After that, the current string p = αβ changes to βRα, where the length of β is x, and the length of α is n - x. In other words, the suffix of the length x of string p is reversed and moved to the beginning of the string. For example, after the operation «shift 4» the string «abcacb» will be changed with string «bcacab », since α = ab, β = cacb, βR = bcac.

Explorers are afraid that if they apply too many operations «shift», the lock will be locked forever. They ask you to find a way to get the string t on the screen, using no more than 6100 operations.

Input

The first line contains an integer n, the length of the strings s and t (1 ≤ n ≤ 2 000).

After that, there are two strings s and t, consisting of n lowercase Latin letters each.

Output

If it is impossible to get string t from string s using no more than 6100 operations «shift», print a single number - 1.

Otherwise, in the first line output the number of operations k (0 ≤ k ≤ 6100). In the next line output k numbers xi corresponding to the operations «shift xi» (0 ≤ xi ≤ n) in the order in which they should be applied.

Examples

input

Copy

6
abacbb
babcba

output

4
6 3 2 3

input

Copy

3
aba
bba

output

-1

In the first example, after applying the operations, the string on the screen will change as follows:

abacbb $\text{[math]}$ bbcaba
bbcaba $\text{[math]}$ ababbc
ababbc $\text{[math]}$ cbabab
cbabab $\text{[math]}$ babcba

题意：给定一个字符串，每次可以执行shift操作，这个操作接受一个参数x，表示将这个字符串的前x位提取出来，放到原字符串的后面，同时原字符串的另一部分翻转过来。操作次数不能大于6100次。问能否将字符串转换为给定的状态。

题解：构造法。很明显，如果源字符串与目标字符串有多段不同，那么无法实现。即如果源字符串与目标字符串有不同的字母或相同的字符数量不同，那么无法实现。

考虑如何构造一组合法解。问题的操作次数上界是3n。

假设当前字符串$s$形如$b\ldots p\ldots$，其中$b$是$t$的前缀，$pb$是$t$的后缀，$p$的下标为$x$。先$shift(n)$，$s=\ldots p\ldots b^R$，再$shift(x−1)$, $s=b\ldots p$，最后$shift(1)$，$s=pb\ldots$。

$I d e a :$

还是举个例子比较容易理解：

从后往前构造：假设已经构造出了字符串$XyZ$，前缀$X$是$t$的后缀，下面要把$y$加进去：

翻转整个串，得到字符串$Z'yX$；
翻转$X'$，得到$XZ'y$；
翻转$y$，得到$yXZ'$。

官方题解操作次数2.5n：

通过5次操作，可以在任意子串的前后各加上一个字符，所以可以利用这个性质，从中间开始构造这个字符串，如果最后字符串反了的话，就再进行一次操作翻转回来。

posted @ 2018-03-03 16:13 baka 阅读(506) 评论(0) 编辑收藏举报

刷新页面返回顶部

baka

⑨

Codeforces Round #467 Div.2题解

公告