【字符串】Lyndon 分解

题目描述

定义 Lyndon Word：\(s\) 是 Lyndon Word 当且仅当 \(s\) 是其所有后缀中最小的一个串。

给定字符串 \(s\) ，请把这个字符串分成若干个子串，使得每个子串都是 Lyndon Word 。并且从左到右每个字符串都大于等于下一个。

最后输出每一个子串右端点异或和。

\(1 \leq n \leq 5 \times 10^6\) 。

算法描述

此处使用时间复杂度 \(\Theta(n)\) ，空间复杂度 \(\Theta(1)\) （不记录划分方案）的方法：Duval 算法

首先可以证明 Lyndon 分解存在且唯一。

我们使用 \(i,j,k\) 三个指针， \([1,i - 1]\) 代表前面已经定好的串；\([i,k]\) 代表正在划分的串，\([k + 1,n]\) 代表没有加入的串。

我们断言，\([i,k]\) 既然没有被确定，一定会形如 \(uuu\dots v\) （后面解释），其中 \(u\) 是一个定长子串，\(v\) 是一个没有确定的子串，其中最后一个字符 （也就是 \(k\)） 和 \(u\) 的相应位置不一定一样，前面都一样。此时 \(j\) 就指向这一位置：

首先我们要知道一件事情：像 \(uuu\) 这样并列相等的串一定要被分开，因为 \(uu\) 并不是一个 Lyndon 串。（后缀 \(u < uu\)）

也就是说， \(j\) 就是 \(u\) 这样的串中和 \(k\) ”同步匹配“ 的指针，现在我们来讨论 \(j,k\) 的大小关系：

• \(s_j < s_k\) ：容易发现如果将 \(k\) 分出去，就不满足 "前面大于后面" 这个性质，所以 \([i,k]\) 要分在一起。所以从 \(k + 1\) 开始，\([i,k]\) 整体变成了一个串 \(u'\)，将指针 \(j = i\)。

• \(s_j > s_k\) ：发现如果将 \(k\) 和前面的串划分成一个，就会出现后缀比整体小的情况，所以确定前面所有 \(u\) 的划分结果，将这些 \(u\) 划分出去，具体方法是将 \(i += (k - j)\) 直到大于 \(j\) 为止。

• \(s_j = s_k\) ：没有问题，继续匹配下一个 ，\(j = j + 1,k = k + 1\) 。

由此还可以得出每次划分时 \((k - j)\) 就是串长，\(i\) 就是开头位置。因为每次 \(j\) 左移至 \(i\) 时中间的部分都划进了一个串。

由此解答前面的问题，只有在 \(k - j\) 等于某个值的时候，对比到很多次的 \(s_j = s_k\) ，\([j,k]\) 像一个滑动窗口一样右移，以至于 \(j\) 已经超过了原来 \(k\) 的位置，就会形成一个周期 \(u\)。

具体在实现代码的时候，采用枚举 \(i\) 的方法，对于每个 \(i\) ，从 \(j = i,k = i + 1\) 开始扫描，扫到 \(s_j > s_k\) 为止，然后移动 \(i\) 。

时间复杂度 \(\Theta(n)\) ，证明详见 OI-Wiki。

#include<bits/stdc++.h>
using namespace std;
const int N = 5e6 + 5;
char s[N];
int n;
vector <int> rt;
int main()
{
	scanf("%s",s + 1);
	n = strlen(s + 1);
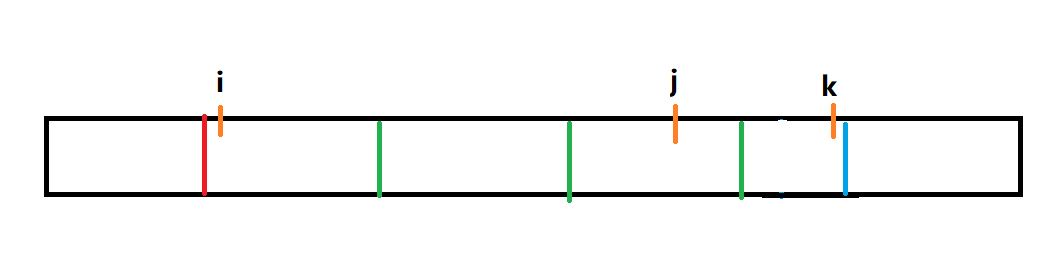
	int i = 1,j,k;
	while(i <= n)
	{
		for(j = i,k = i + 1;k <= n && s[j] <= s[k];)
		{
			if(s[j] == s[k]) j++,k++;
			else j = i,k++;
		}
		for(int len = k - j;i <= j;i += (k - j)) rt.push_back(i + len - 1);
	}
	int res = 0;
	for(auto in : rt) res ^= in;
	cout<<res;
	return 0;
}

用处

目前蒟蒻作者只知道这个可以解决一个串的最小表示法问题：

我们知道每一个 Lyndon 子串小于所有后缀，所以从每个子串的开头一定是最优的，然而我们又知道前面的子串大于等于后面的子串，所以直接取最后一个子串开头即可。