线代相关的 3 道神题

高消神题

考虑设 $f_{x,y}$ 为点在 $(x,y)$ 时的期望步数，有：

\[f_{x,y} = p_1f_{x + 1,y} + p_2f_{x,y + 1} + p_3f_{x - 1,y} + p_4f_{x,y - 1} + 1 \]

直接高斯消元求出，复杂度 $\Theta(R^6)$ 。不能过。

对于这种项数很少的有一种东西叫做 “带状消元”，自行了解。

这里考虑消元的各项都有递推关系，我们考虑主元，从左到右，从上到下转移，对于每一行，将最左边的在圆内的点作为主元，用 $f_{x,y},f_{x - 1,y},f_{x,y - 1},f_{x + 1,y}$ 来推出 $f_{x,y + 1}$ ，移项即可，如图，黑点就是主元，蓝色代表转移方向：

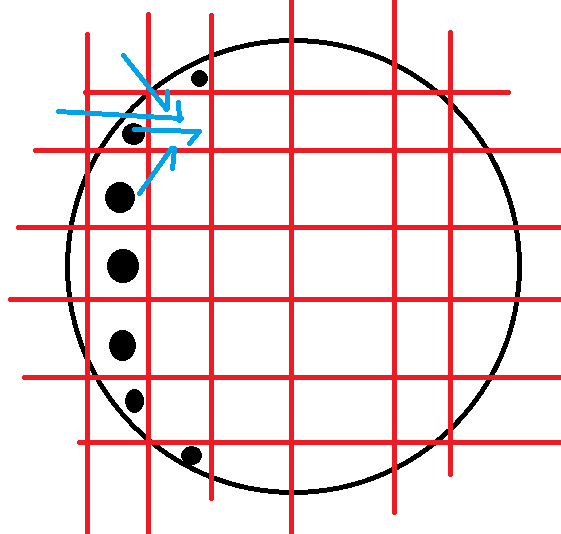
我们容易发现主元有 $2R + 1$ 个，每一行末尾第一个超出圆的点也可以被主元表示，但是值为 $0$ 。可以列出一个方程，这样就可以列 $2R + 1$ 个方程，高斯消元就可以解出主元，由于我们知道 $f_{0,0}$ 关于主元的表达式，直接代入即可。

时间复杂度 $\Theta(R^3)$ 。

#include<bits/stdc++.h>
using namespace std;
const int N = 55,MOD = 1e9 + 7;
typedef long long ll;
int M,len,R,a1,a2,a3,a4;
ll p1,p2,p3,p4;
inline ll ksm(ll base,int pts)
{
    ll ret = 1;
    for(;pts > 0;pts >>= 1,base = base * base % MOD)
        if(pts & 1)
            ret = ret * base % MOD;
    return ret;
 } 
struct Vector{
    ll a[N * 2];
}f[2 * N][2 * N],one;
ll V[N * 2][N * 2];
inline Vector operator +(Vector x,Vector y)
{
    Vector z;
    for(int i = 1;i <= len + 1;i++) z.a[i] = (x.a[i] + y.a[i]) % MOD;
    return z;
}
inline Vector operator -(Vector x,Vector y)
{
    Vector z;
    for(int i = 1;i <= len + 1;i++) z.a[i] = (x.a[i] - y.a[i] + MOD) % MOD;
    return z;
}
inline Vector operator *(ll x,Vector y)
{
    Vector z;
    for(int i = 1;i <= len + 1;i++) z.a[i] = y.a[i] * x % MOD;
    return z;
}
inline bool in(int x,int y) {return x * x + y * y <= R * R;}
inline void Gauss()
{
    for(int i = 1;i <= len;i++)
    {
        int tmp = i;
        while(tmp < len && V[tmp][i] == 0) tmp++;
        swap(V[tmp],V[i]);
        ll now = ksm(V[i][i],MOD - 2);
        for(int j = 1;j <= len + 1;j++) V[i][j] = V[i][j] * now % MOD;
        for(int j = 1;j <= len;j++)
        {
            if(j == i) continue;
            ll rate = V[j][i];
            for(int k = 1;k <= len + 1;k++) V[j][k] = (V[j][k] - V[i][k] * rate % MOD + MOD) % MOD;
        } 
    }
}
int main()
{
    cin>>R>>a1>>a2>>a3>>a4;
    len = 2 * R + 1; M = R + 1;
    ll inv = ksm(a1 + a2 + a3 + a4,MOD - 2);
    p1 = a1 * inv % MOD; p2 = a2 * inv % MOD; p3 = a3 * inv % MOD; p4 = a4 * inv % MOD;
    one.a[len + 1] = 1;
    for(int i = R;i >= -R;i--)
        for(int j = -R;j <= R;j++)
            if(in(i,j) && !in(i,j - 1)) f[i + M][j + M].a[i + M] = 1;
    for(int j = -R;j <= R;j++)
        for(int i = R;i >= -R;i--)
            if(in(i,j))
            {
                f[i + M][j + M + 1] = ksm(p4,MOD - 2) * (f[i + M][j + M] - p1 * f[i + M + 1][j + M] - p2 * f[i + M][j + M - 1] - p3 * f[i + M - 1][j + M] - one);
            }
    for(int j = -R;j <= R;j++)
        for(int i = R;i >= -R;i--)
            if(in(i,j) && !in(i,j + 1))
            {
                for(int k = 1;k <= len;k++) V[i + M][k] = f[i + M][j + M + 1].a[k];
                V[i + M][len + 1] = MOD - f[i + M][j + M + 1].a[len + 1];
            }
    Gauss();
    ll ans = 0;
    for(int i = 1;i <= len;i++) ans = (ans + f[M][M].a[i] * V[i][len + 1] % MOD) % MOD;
    ans = (ans + f[M][M].a[len + 1]) % MOD; 
    cout<<ans;
    return 0; 
}

矩阵树神题

Mirror Box

手模 $114$ 个图可以发现一些规律：

图可以看作是格点与格点连边，将格点黑白染色，则只能同色连边
想要每条棱都被覆盖，不能有环
想做到相邻两个相通，某一种颜色的格点要全部连通。

知道这些，做法就十分简单：对于确定的边，并查集处理，不确定的方格，两种边都有可能，将并查集上这两个连通块间连一条边，对于这种颜色，最后跑一遍矩阵树即可。

由于没填的格子不超过 $200$ 个，所以并查集缩成的节点数是 $\Theta(k)$ 的。

我们观察到两种颜色不可能同时连通，一种颜色有了生成树，另一种颜色的连法唯一。

所以答案就是两种颜色分别的生成树数量之和。

时间复杂度 $\Theta(nm\alpha(nm) + k^3)$ 。

#include<bits/stdc++.h>
using namespace std;
const int N = 305;
int n,m,MOD,sym[N * N];
char s[N][N];
struct UFS{
    int fa[N * N];
    inline void init() {for(int i = 1;i <= (n + 1) * (m + 1);i++) fa[i] = i;}
    inline int find(int x) {return (fa[x] == x) ? x : fa[x] = find(fa[x]);}
    inline void unionn(int x,int y) {x = find(x); y = find(y); fa[x] = y;}
}t;
typedef long long ll;
inline ll ksm(ll base,int pts)
{
    ll ret = 1;
    for(;pts > 0;pts >>= 1,base = base * base % MOD)
        if(pts & 1)
            ret = ret * base % MOD;
    return ret;
}
struct Graph{
    ll V[3 * N][3 * N],cnt;
    inline void add(int x,int y)
    {
        V[x][x]++; V[y][y]++; V[x][y]--; V[y][x]--;
    }
    inline ll getdet()
    {
        ll ret = 1;
        for(int i = 1;i <= cnt - 1;i++)
        {
            int tmp = i;
            while(tmp < cnt - 1 && V[tmp][i] == 0) ++tmp;
            if(tmp ^ i) swap(V[i],V[tmp]),ret = MOD - ret;
            ret = ret * V[i][i] % MOD;
            for(int j = i + 1;j <= cnt - 1;j++)
            {
                ll rate = V[j][i] * ksm(V[i][i],MOD - 2) % MOD;
                for(int k = 1;k <= cnt - 1;k++) V[j][k] = (V[j][k] - V[i][k] * rate % MOD + MOD) % MOD;
            } 
        }
        return ret;
    }
}g[2];
inline int num(int x,int y) // 格点 (x,y) 左上角
{
    return (x - 1) * (m + 1) + y;
} 
int main()
{
    cin>>n>>m>>MOD;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            cin>>s[i][j];
    t.init();
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
        {
            if(s[i][j] == '/') t.unionn(num(i,j + 1),num(i + 1,j));
            else if(s[i][j] == '\\') t.unionn(num(i,j),num(i + 1,j + 1));
        }
    for(int i = 1;i <= n + 1;i++)
        for(int j = 1;j <= m + 1;j++)
            if(t.find(num(i,j)) == num(i,j) && ((i + j) & 1))
                sym[num(i,j)] = ++g[1].cnt;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            if(s[i][j] == '*')
            {
                if(t.find(num(i,j)) != t.find(num(i + 1,j + 1)) && ((i + j) & 1))
                    g[(i + j) & 1].add(sym[t.find(num(i,j))],sym[t.find(num(i + 1,j + 1))]);
                if(t.find(num(i + 1,j)) != t.find(num(i,j + 1)) && ((i + j) & 1 ^ 1))
                    g[(i + j) & 1 ^ 1].add(sym[t.find(num(i + 1,j))],sym[t.find(num(i,j + 1))]);
            }
    for(int i = 1;i <= n + 1;i++)
        for(int j = 1;j <= m + 1;j++)
            if(t.find(num(i,j)) == num(i,j) && !((i + j) & 1))
                sym[num(i,j)] = ++g[0].cnt;
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            if(s[i][j] == '*')
            {    
                if(t.find(num(i,j)) != t.find(num(i + 1,j + 1)) && !((i + j) & 1))
                    g[(i + j) & 1].add(sym[t.find(num(i,j))],sym[t.find(num(i + 1,j + 1))]);
                if(t.find(num(i + 1,j)) != t.find(num(i,j + 1)) && !((i + j) & 1 ^ 1))
                    g[(i + j) & 1 ^ 1].add(sym[t.find(num(i + 1,j))],sym[t.find(num(i,j + 1))]);
            }
    cout<<(g[0].getdet() + g[1].getdet()) % MOD;
    return 0;
}

LGV 神题

Ascending Matrix

给定 $n,m,k,r,c,v$ ，求有多少个正整数构成的 $n \times m$ 矩阵，满足值域为 $[1,k]$ ，且满足：

每行单调不降
每列单调不降
$a_{r,c} = v$

答案模 $998244353$ 。

$1 \leq n,m \leq 200,1 \leq k \leq 100$ 。

以下过程建议读者全程画图模拟。

考虑如果没有 $(r,c) = v$ 这个限制，我们将格子的顶点编号为 $1 \sim n + 1$ 行，则每行列单调不降等价于从 $(n + 1,1)$ 到 $(1,m + 1)$ 选 $k - 1$ 条不交叉的路径（可以相交）。

最上面的路径代表左侧是 $ \leq 1$ 的格子，右侧是 $> 1$ 的格子。

考虑将不交叉转化为彻底不交，就是将原来横竖方向的重叠分开，将第 $i$ 条线向右下平移 $i - 1$ 格即可，起点变成 $(n + i,i)$ ，终点变成 $(i,m + i)$ ，求不相交路径组。

容易发现和 LGV 模板题一样，这题还是只有起、终点顺序对应才有解，所以直接考虑 LGV 即可。

现在加上 $(r,c) = v$ ，相当于要求有 $v - 1$ 条路径要在 $(r,c)$ 格点左上方（或经过），我们将其平移 $v - 1$ 格得到 $(r + v - 1,c + v - 1)$ ，由于不交的性质，观察得到必须有 $v - 1$ 条路径在这个点的 左上方（不经过）。

不经过是因为前面的 $v - 1$ 条路径最多向右下平移了 $(v - 2)$ 格，这个点平移了 $(v - 1)$ 格，如果经过，原图上实际在下方，不满足要求。

同理，原本该在下方的路径如果经过这个点，在原图上就会在这个点上方，也不满足，所以这个点不能被经过。

分析到这里可能有一点小问题：限制点被移动后，对于前面的点，由于起点比较高，可能出现在限制点上方，但是这条路径不满足原来的限制，这样的情况，如何避免？

假设出现了这样的情况，可以发现由于所有路径没有交点，那么后面的路径在这条平移对角线上一定依次往下，第 $v - 1$ 条路径一定会在限制点的下方（或经过），这个路径集就不满足要求了。所以这种方法可以排除掉所有不合法的情况。

至于强制 $v - 1$ 个点，统计的时候用变元，将路径条数转化为 $(ax + b)$ ，$a$ 是上方的路径， $b$ 是下方的。最后求 $[x^{v - 1}]$ 系数即可。

这个多项式次数为 $k - 1$ ，复杂度是 $\Theta(k^5)$ 的，难以通过。

所以我们只需要求 $v - 1$ 次系数，考虑拉格朗日插值，我们代入 $k$ 个系数进去，跑 $k$ 次 LGV ，然后假设每次得到的点值是 $a_i$ ，我们插出系数即可。

时间复杂度 $\Theta(k^4)$ 。

拉格朗日插值求系数：

假设我们有 $k$ 个点值是 $y_1 \sim y_k$ ，横坐标是 $x_1 \sim x_k$ ，考虑拉插式子：

\[f(X) = \sum_i y_i \frac{\prod_{j \neq i}(X - x_j)}{\prod_{j \neq i}(x_i - x_j)} \]

提出常数项，设为 $a_i$：

\[a_i = \frac {y_i}{\prod_{j \neq i}(x_i - x_j)} \]

可以 $\Theta(n^2)$ 求出。

设 $g(X) = \prod_i (X - x_i)$ ，则原式为：

\[f(X) = \sum_i a_i \frac{g(X)}{X - x_i} \]

$g(X)$ 可以简单地 $\Theta(n^2)$ 递推。

我们设 $p_i(X) = \frac {g(X)}{X - x_i}$ ，如果能够 $\Theta(n)$ 推出 $p_i(X)$ ，那么就枚举 $i$ ，$\Theta(n^2)$ 推出多项式 $f$ 。

移项发现：

\[(X - x_i)p_i(X) = g(X) \]

两边同时取项：

\[[X^{j - 1}]p_i - x_i[X^j]p_i = [X^j]g \]

最终得到：

\[[X^j]p_i = \frac{[X^{j - 1}p_i - [X^j]g]}{x_i} \]

$[X^0]p_i = \frac{[X^0]g}{-x_i}$ ，递推即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 405,MOD = 998244353;
typedef long long ll;
int n,m,k,r,c,v,ptx,pty;
pair <ll,ll> poly[N][N];
inline ll ksm(ll base,int pts)
{
	ll ret = 1;
	for(;pts > 0;pts >>= 1,base = base * base % MOD)
		if(pts & 1)
			ret = ret * base % MOD;
	return ret;
} 
struct Binom{
	ll frac[N * 3],inv[N * 3];
	inline void init()
	{
		frac[0] = inv[0] = 1;
		for(int i = 1;i < N * 3;i++) frac[i] = frac[i - 1] * i % MOD;
		inv[N * 3 - 1] = ksm(frac[N * 3 - 1],MOD - 2);
		for(int i = N * 3 - 2;i >= 1;i--) inv[i] = inv[i + 1] * (i + 1) % MOD;
	}
	inline ll C(int y,int x)
	{
		if(y < 0 || x < 0 || y < x) return 0ll;
		return frac[y] * inv[x] % MOD * inv[y - x] % MOD;
	}
	inline ll path(int x,int y,int xx,int yy)
	{
		if(x < xx) return 0ll; if(y > yy) return 0ll;
		return C(x - xx + yy - y,yy - y);
	}
}B;
struct Matrix{
	ll a[N][N],len;
	inline ll getdet()
	{
		ll ret = 1;
		for(int i = 1;i <= len;i++)
		{
			int tmp = i;
			while(tmp < len && a[tmp][i] == 0) tmp++;
			if(tmp ^ i) swap(a[tmp],a[i]),ret = MOD - ret;
			ret = ret * a[i][i] % MOD;
			for(int j = i + 1;j <= len;j++)
			{
				ll rate = a[j][i] * ksm(a[i][i],MOD - 2) % MOD;
				for(int k = 1;k <= len;k++) a[j][k] = (a[j][k] - a[i][k] * rate % MOD + MOD) % MOD;
			}
		}
		return ret;
	}
}g;
struct Lagrange{
	ll y[N],f[N],g[N],a[N],p[N];
	inline void solve()
	{
		for(int i = 0;i <= k;i++)
		{
			a[i] = 1;
			for(int j = 0;j <= k;j++)
				if(j != i)
					a[i] = a[i] * (i - j + MOD) % MOD;
			a[i] = ksm(a[i],MOD - 2) * y[i] % MOD;
		}
		g[0] = 1;
		for(int i = 0;i <= k;i++)
		{
			for(int j = i + 1;j >= 1;j--) 
				g[j] = (g[j] * (MOD - i) % MOD + g[j - 1]) % MOD;
			g[0] = g[0] * (MOD - i) % MOD;
		}
		for(int i = 0;i <= k;i++)
		{
			ll inv = ksm(i,MOD - 2);
			if(!inv) 
			{
				for(int j = 0;j <= k;j++) p[j] = g[j + 1];
			}
			else
			{
				p[0] = g[0] * ksm(MOD - i,MOD - 2) % MOD;
				for(int j = 1;j <= k;j++) 
					p[j] = (p[j - 1] - g[j] + MOD) * inv % MOD;
			}
			for(int j = 0;j <= k;j++)
				f[j] = (f[j] + p[j] * a[i] % MOD) % MOD;
		}
	}
}t;
int main()
{
	cin>>n>>m>>k>>r>>c>>v;
	ptx = r + v - 1; pty = c + v - 1;
	B.init();
	g.len = k - 1;
	for(int i = 1,sx,sy;i <= g.len;i++)
	{
		sx = n + i; sy = i;	
		for(int j = 1,tx,ty;j <= g.len;j++)
		{
			tx = j; ty = m + j;
			ll a = 0,b = (B.path(sx,sy,tx,ty) - B.path(sx,sy,ptx,pty) * B.path(ptx,pty,tx,ty) % MOD + MOD) % MOD;
			for(int o = 1;o < min(ptx,pty);o++)
				a = (a + B.path(sx,sy,ptx - o,pty - o) * B.path(ptx - o,pty - o,tx,ty) % MOD) % MOD;
			b = (b - a + MOD) % MOD;
			poly[i][j] = make_pair(a,b);
		}
	}
	for(int i = 0;i <= k;i++)
	{
		for(int j = 1;j <= g.len;j++)
			for(int o = 1;o <= g.len;o++)
				g.a[j][o] = (poly[j][o].first * i % MOD + poly[j][o].second) % MOD;
		t.y[i] = g.getdet();
	}
	t.solve();
	cout<<t.f[v - 1];
	return 0;
}

posted @ 2023-12-27 09:06 The_Last_Candy 阅读(7) 评论(0) 编辑收藏举报

刷新页面返回顶部

The_Last_Candy

线代相关的 3 道神题

高消神题

矩阵树神题

LGV 神题

拉格朗日插值求系数：

公告