【数据结构】lxl 的 DS 修炼

线段树 & 平衡树

用线段树/平衡树维护的序列问题可以分为两类：

1.静态型：维护一个类似于 $\sum_{l, r} . . . .$ 的值，或者是多次询问区间或全局的一些特征值。

2.动态型：支持动态修改和动态询问区间信息的类型。

对于静态型，我们通常首先思考怎样求单个区间的答案值，同理，动态型通常先考虑不带修，也就是一个序列怎么做。

对于一个难以维护的题目，我们可以先写出要维护的信息，然后画出一个信息和另一个的依赖推导关系，最后得到闭包求出答案。

例如：

「Wdsr-2.7」文文的摄影布置

这题可以转化为：求区间内任意三元组 $(i, j, k) (i < j < k)$ 的 $A_{i} - B_{j} + A_{k}$ 最大值。

考虑静态问题，观察能不能计算跨过分治中心的答案，架构序列分治的模型。我们发现有四种情况：

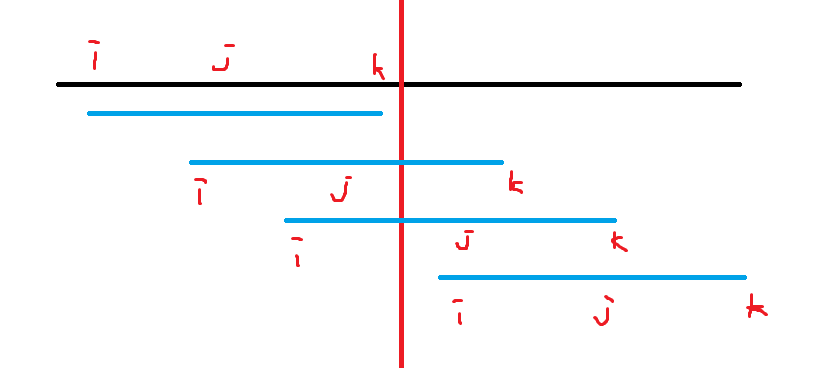
考虑 $i, j, k$ 全在左右边，就是左右边单独的答案 $max$ 。考虑 $i, j$ 在左边的情况：

首先由于 $k$ 一定在右边，取 $max a_{k}$ 一定是最优的。所以左边要求 $a_{i} - b_{j}$ 的最大值。

考虑左边的区间，同样地，我们发现， $a_{i} - b_{j}$ 要么就是左边儿子的答案，要么就是右边儿子的答案，要么就是左边 $max a_{i}$ 减去右边 $min b_{j}$ ，这样我们将问题转化为了求 $a, b$ 的最值，成功解决。

其他情况同样讨论即可。

按照上面的说法，这张图画下来就应该是这样的：

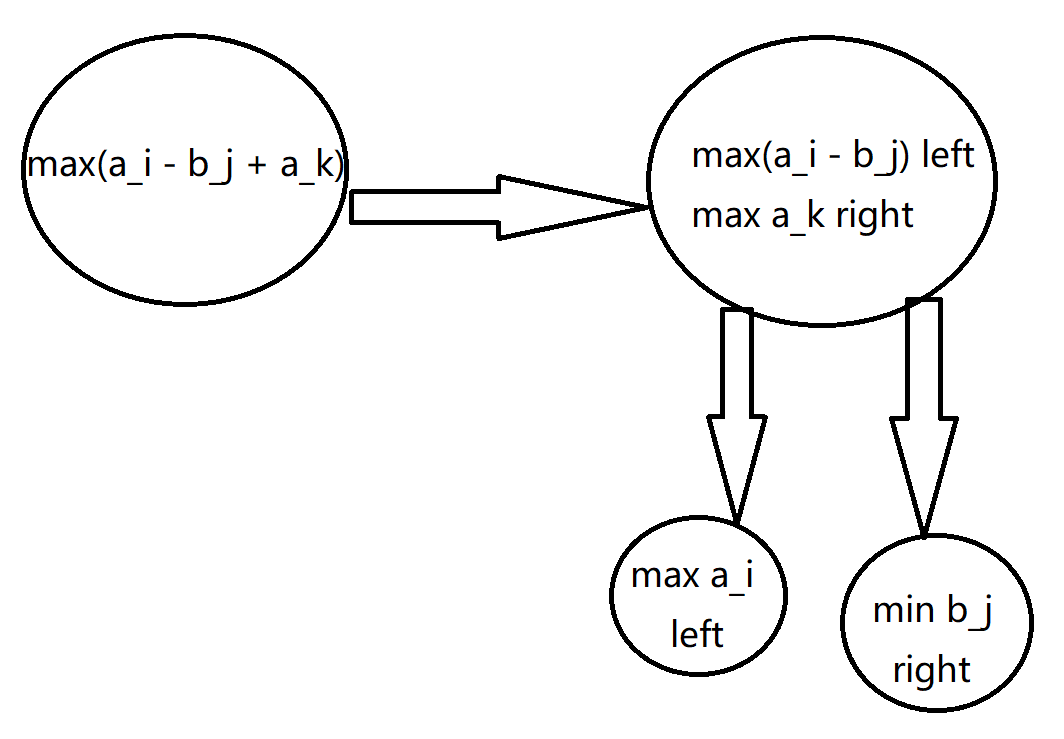
展开到最后一步，理清思路，再返回实现代码，很快就可以做完。

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5,inf = 0x3f3f3f3f;
int n,m,A[N],B[N];
struct Node{
    int mxa,mnb,ansij,ansjk,ans;
};
Node operator +(Node x,Node y)
{
    Node z;
    z.mxa = max(x.mxa,y.mxa);
    z.mnb = min(x.mnb,y.mnb);
    z.ansij = max(max(x.ansij,y.ansij),x.mxa - y.mnb);
    z.ansjk = max(max(x.ansjk,y.ansjk),y.mxa - x.mnb);
    z.ans = max(max(x.ans,y.ans),max(x.ansij + y.mxa,x.mxa + y.ansjk));
    return z;
}
struct Segment_Tree{
    Node a[N << 2];
    inline void pushup(int pos) {a[pos] = a[pos << 1] + a[pos << 1 | 1];}
    inline void modify(int l,int r,int x,int k,int type,int pos)
    {
        if(l == r) {if(type == 1) a[pos].mxa = k; else a[pos].mnb = k; return;}
        int mid = (l + r) >> 1;
        if(x <= mid) modify(l,mid,x,k,type,pos << 1);
        else modify(mid + 1,r,x,k,type,pos << 1 | 1);
        pushup(pos);
    }
    inline Node query(int l,int r,int L,int R,int pos)
    {
        if(L <= l && r <= R) return a[pos];
        int mid = (l + r) >> 1; Node ret = {-inf,-inf,-inf,-inf,-inf};
        if(L <= mid) ret = query(l,mid,L,R,pos << 1);
        if(R > mid) {if(ret.mxa == -inf) ret = query(mid + 1,r,L,R,pos << 1 | 1); else ret = ret + query(mid + 1,r,L,R,pos << 1 | 1);}
        return ret;
    }
    inline void build(int l,int r,int pos)
    {
        if(l == r) {a[pos].mxa = A[l]; a[pos].mnb = B[l]; a[pos].ansij = a[pos].ansjk = a[pos].ans = -inf; return;}
        int mid = (l + r) >> 1;
        build(l,mid,pos << 1); build(mid + 1,r,pos << 1 | 1);
        pushup(pos); 
    }
}t;
int main()
{
    cin>>n>>m;
    for(int i = 1;i <= n;i++) cin>>A[i];
    for(int i = 1;i <= n;i++) cin>>B[i];
    t.build(1,n,1);
    Node ret = t.query(1,n,1,n,1);
    for(int i = 1,op,x,y;i <= m;i++)
    {
        cin>>op>>x>>y;
        if(op == 1 || op == 2) t.modify(1,n,x,y,op,1);
        else cout<<t.query(1,n,x,y,1).ans<< '\n';
    }
    return 0;
 }

技巧

[HNOI2011] 括号修复 / [JSOI2011]括号序列

按照套路，首先考虑静态怎么做，发现可以转化：

尽量匹配所有的括号，删掉，剩下的一定形如 ))))))...((((((

所以我们只需要改成 ()()()()()()()()()()()()...

假设剩右括号有 $p$ 个，左括号有 $q$ 个，我们可以发现答案就是 $⌈ \frac{p}{2} ⌉ + ⌈ \frac{q}{2} ⌉$ 。

解决了静态序列的问题，容易看出来这个东西是好合并的，讨论一下即可。

分开考虑维护几个操作：

1.Replace

区间推平，线段树上用一个标记即可，推平后整个区间的值可以 $Θ (1)$ 计算。

2.Swap

翻转串，这里意识到需要用平衡树，平衡树上 tag 照样可以维护第一个，所以套文艺平衡树即可，再用一个 tag。

3.Invert

取反，这个很不好做，先前再 Flower's Land 当中见过类似套路，观察到取反再取反就不变，状态数 $Θ (1)$ 个，我们同时维护 $2$ 种状态的答案，取反时打标记再交换答案即可。

这样我们就用平衡树维护了操作，可以回答询问。但是笔者仍然调了两个小时，最后发现，问题出在 Swap 上，线段树区间操作的两大要求就是 懒标记的可并性 和 当前区间被整个包含时 $Θ (1)$ 得出答案 。就是说翻转后的区间答案不一样，我们要求 $Θ (1)$ 算出，怎么办呢？

发现翻转这个东西也是只有 $2$ 个状态的操作，所以我们再同时维护出翻转前后的答案即可。

这样，我们用 $3$ 个标记， $4$ 个状态大常数 $Θ (n \log n)$ 地维护出了信息。

注意标记顺序要将 Invert 放在第一位，并且取反后要将推平标记也取反。推平后要将取反标记归零。

#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 5;
int n,q,a[N];
char s[N];
struct fhq{//正/反，换/不换 
    int val[2][N],valpre[2][2][N],valsuf[2][2][N],tot = 0,lc[N],rc[N],hp[N],siz[N],tagflip[N],tagrev[N],tagcov[N],root = 0,y,z,w,p;
    inline void pushup(int pos)
    {
        valpre[0][0][pos] = valpre[0][0][lc[pos]] + max(0,valpre[0][0][rc[pos]] + (val[0][pos] == 1 ? 1 : -1) - valsuf[0][0][lc[pos]]);
        valsuf[0][0][pos] = valsuf[0][0][rc[pos]] + max(0,valsuf[0][0][lc[pos]] + (val[0][pos] == 0 ? 1 : -1) - valpre[0][0][rc[pos]]);
        valpre[0][1][pos] = valpre[0][1][lc[pos]] + max(0,valpre[0][1][rc[pos]] + (val[1][pos] == 1 ? 1 : -1) - valsuf[0][1][lc[pos]]);
        valsuf[0][1][pos] = valsuf[0][1][rc[pos]] + max(0,valsuf[0][1][lc[pos]] + (val[1][pos] == 0 ? 1 : -1) - valpre[0][1][rc[pos]]);
        swap(lc[pos],rc[pos]);
        valpre[1][0][pos] = valpre[1][0][lc[pos]] + max(0,valpre[1][0][rc[pos]] + (val[0][pos] == 1 ? 1 : -1) - valsuf[1][0][lc[pos]]);
        valsuf[1][0][pos] = valsuf[1][0][rc[pos]] + max(0,valsuf[1][0][lc[pos]] + (val[0][pos] == 0 ? 1 : -1) - valpre[1][0][rc[pos]]);
        valpre[1][1][pos] = valpre[1][1][lc[pos]] + max(0,valpre[1][1][rc[pos]] + (val[1][pos] == 1 ? 1 : -1) - valsuf[1][1][lc[pos]]);
        valsuf[1][1][pos] = valsuf[1][1][rc[pos]] + max(0,valsuf[1][1][lc[pos]] + (val[1][pos] == 0 ? 1 : -1) - valpre[1][1][rc[pos]]);
        swap(lc[pos],rc[pos]);
        siz[pos] = siz[lc[pos]] + siz[rc[pos]] + 1;
    }
    inline void change_flip(int pos)
    {
        if(!pos) return;
        swap(val[0][pos],val[1][pos]);
        swap(valpre[0][0][pos],valpre[0][1][pos]); swap(valsuf[0][0][pos],valsuf[0][1][pos]);
        swap(valpre[1][0][pos],valpre[1][1][pos]); swap(valsuf[1][0][pos],valsuf[1][1][pos]);
        tagflip[pos] ^= 1;
        if(tagcov[pos] != -1) tagcov[pos] ^= 1;
    }
    inline void change_rev(int pos)
    {
        if(!pos) return;
        swap(lc[pos],rc[pos]); 
        swap(valpre[0][0][pos],valpre[1][0][pos]); swap(valpre[0][1][pos],valpre[1][1][pos]);
        swap(valsuf[0][0][pos],valsuf[1][0][pos]); swap(valsuf[0][1][pos],valsuf[1][1][pos]);
        tagrev[pos] ^= 1;
    }
    inline void change_cov(int pos,int x)
    {
        if(!pos) return;
        val[0][pos] = x; val[1][pos] = x ^ 1;
        if(x == 0) 
        {
            valpre[0][0][pos] = 0; valsuf[0][0][pos] = siz[pos];
            valpre[0][1][pos] = siz[pos]; valsuf[0][1][pos] = 0;
            valpre[1][0][pos] = 0; valsuf[1][0][pos] = siz[pos];
            valpre[1][1][pos] = siz[pos]; valsuf[1][1][pos] = 0;
        }
        else
        {
            valpre[0][0][pos] = siz[pos]; valsuf[0][0][pos] = 0;
            valpre[0][1][pos] = 0; valsuf[0][1][pos] = siz[pos];
            valpre[1][0][pos] = siz[pos]; valsuf[1][0][pos] = 0;
            valpre[1][1][pos] = 0; valsuf[1][1][pos] = siz[pos];
        }
        tagcov[pos] = x; tagflip[pos] = 0;
    }
    inline void pushdown(int pos)
    {
        if(tagflip[pos])
        {
            change_flip(lc[pos]); change_flip(rc[pos]);
            tagflip[pos] = 0;
        }
        if(tagrev[pos])
        {
            change_rev(lc[pos]); change_rev(rc[pos]);
            tagrev[pos] = 0;
        }
        if(tagcov[pos] != -1)
        {
            change_cov(lc[pos],tagcov[pos]); change_cov(rc[pos],tagcov[pos]);
            tagcov[pos] = -1;
        }
    }
    inline void split(int &x,int &y,int k,int pos)
    {
        if(!pos) {x = y = 0; return;}
        pushdown(pos);
        if(siz[lc[pos]] + 1 <= k) x = pos,split(rc[x],y,k - siz[lc[pos]] - 1,rc[pos]);
        else y = pos,split(x,lc[y],k,lc[pos]);
        pushup(pos);
    }
    inline int merge(int x,int y)
    {
        pushdown(x); pushdown(y);
        if(!x || !y) return x + y;
        if(hp[x] < hp[y])
        {
            rc[x] = merge(rc[x],y);
            pushup(x);
            return x;
        }
        else
        {
            lc[y] = merge(x,lc[y]);
            pushup(y);
            return y;
        }
    }
    inline int new_node(int x)
    {
        ++tot;
        val[0][tot] = x; val[1][tot] = x ^ 1;
        valpre[0][0][tot] = x; valsuf[0][0][tot] = x ^ 1;
        valpre[0][1][tot] = x ^ 1; valsuf[0][1][tot] = x;
        valpre[1][0][tot] = x; valsuf[1][0][tot] = x ^ 1;
        valpre[1][1][tot] = x ^ 1; valsuf[1][1][tot] = x;
        lc[tot] = rc[tot] = 0;
        siz[tot] = 1;
        hp[tot] = 1ll * rand() * rand();
        return tot;
    }
    inline void ist(int x)
    {
        root = merge(root,new_node(x));
    }
    inline void cover(int l,int r,int x)
    {
        split(y,z,l - 1,root);
        split(w,p,r - l + 1,z);
        change_cov(w,x);
        root = merge(y,merge(w,p));
    }
    inline void reverse(int l,int r)
    {
        split(y,z,l - 1,root);
        split(w,p,r - l + 1,z);
        change_rev(w);
        root = merge(y,merge(w,p));
    }
    inline void flip(int l,int r)
    {
        split(y,z,l - 1,root);
        split(w,p,r - l + 1,z);
        change_flip(w);
        root = merge(y,merge(w,p));
    }
    inline int query(int l,int r)
    {
        split(y,z,l - 1,root);
        split(w,p,r - l + 1,z);
        int nowp = valpre[0][0][w],nows = valsuf[0][0][w];
        root = merge(y,merge(w,p));
        return (nowp + 1) / 2 + (nows + 1) / 2;
    }
}t;
int main()
{
    fill(t.tagcov,t.tagcov + N,-1);
    srand(time(NULL));
    cin>>n>>q;
    scanf("%s",s + 1);
    for(int i = 1;i <= n;i++) a[i] = (s[i] == '(') ? 0 : 1;
    for(int i = 1;i <= n;i++) t.ist(a[i]);
    string op; char d; int x,y;
    for(int i = 1;i <= q;i++)
    {
        cin>>op;
        if(op == "Replace")
        {
            cin>>x>>y>>d;
            t.cover(x,y,(d == ')') ? 1 : 0); 
        }
        else if(op == "Swap")
        {
            cin>>x>>y;
            t.reverse(x,y);
        }
        else if(op == "Invert")
        {
            cin>>x>>y;
            t.flip(x,y);
        }
        else if(op == "Query")
        {
            cin>>x>>y;
            cout<<t.query(x,y)<< '\n'; 
        }
    }
    return 0;
}

ODT/颜色段均摊

考虑一个题是否能用 ODT 的重要条件：

1.每次在遍历颜色段消耗复杂度的时候有没有相应的减少颜色段个数。

2.能不能通过构造两步操作，让程序花费代价并且回到原来的状态。

2 条件如果可以构造出来，就不能直接 ODT ，需要一定的转化或者其他方法。

扫描线

自由度：询问根据几个变量，自由度就为几，例如区间询问 $[l, r]$ 的自由度为 $2$ ，询问区间 $[l, r]$ 中 $\leq k$ 的数字个数，自由度为 $3$ 。

我们称一个 $4 - s i d e$ 的矩形是对于四条边都有限制的矩形，同理， $3 - s i d e$ 的矩形就是有一条边没有限制的矩形。

一个 $4 - s i d e$ 矩形可以通过差分转换为四个 $2 - s i d e$ 矩形。

对于一般的矩形统计问题，静态情况下是二维的，扫描线算法就是将静态问题转化为动态问题，并且降一个维度的算法。动态扫描一维，用数据结构统计另一维，就可以完成对 $4 - s i d e$ 矩形的统计。

CF1000F One Occurrence

长 $n$ 的序列， $m$ 次询问区间有多少个只出现一次的数字。

$1 \leq n, m \leq 5 \times 10^{5}$ 。

接下来讲两种做法：

第一种，我们考虑静态统计，看到 “只出现一次” 经典转化：记录 $p r e_{i}$ 为 $a_{i}$ 在 $i$ 之前出现的位置，就是求区间 $[l, r]$ 中 $p r e_{i} < l$ 的数量，将 $(i, p r e_{i})$ 看作一个点，就是数一个 $3 - s i d e$ 矩形中的点，静态做可以主席树 $Θ (n \log n)$ 解决。

第二种，我们不妨换一个角度，考虑每一种颜色，将区间 $[l, r]$ 视为点 $(l, r)$ ，这种颜色只有在区间中只出现一次时才贡献，所以列举出 $x$ 的出现位置，将会对左右断点在以下范围内的区间产生贡献：

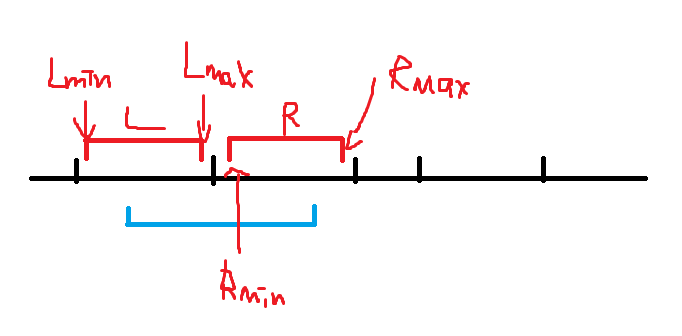
我们发现这个可以表示成一个矩形加的形式，即对左上角为 $(L_{m i n}, R_{m i n})$ ，右上角为 $(L_{m a x}, R_{m a x})$ 这个矩形加 $1$ 。

最后的询问区间就相当于单点询问，由于所有颜色的出现次数和不会超过 $n$ ，所以矩形的个数是 $Θ (n)$ 个的。最后 $Θ (n \log n)$ 扫描线即可。

这种方法的好处在于将刚才的矩形查变成了单点查，转化为了更利于扫描线的形式。

[Ynoi2015] 即便看不到未来

长度为 $n$ 的序列，多次询问 $[l, r]$ 内的数组成的值域中长度为 $[1, 10]$ 的极长连续段的个数。

$1 \leq n, m \leq 10^{6}$ 。

考虑扫描线，扫描右端点，考虑每次将 $a_{r}$ 加入这个值域会有什么影响，发现最多只会影响原来值域在 $[a_{r} - 10, a_{r} + 10]$ 中的数。

考虑在 $[l a s t_{a_{r}} + 1, r]$ 中挑出对于 $x \in [a_{r} - 10, a_{r} + 10]$ ， $x$ 最后一次出现的位置。这样最多有 $20$ 个关键点，将 $[l a s t_{a_{r}} + 1, r]$ 分成了若干段，每一段在加入 $a_{r}$ 前，周围的值域分布是一样的。

只需要求出来 $a_{r}$ 左边连续多少个，右边连续多少个。 $a_{r}$ 的加入带来的影响就是将左边和右边两段合并起来，变成一段更长的而已。相应地进行修改即可。

将询问挂在右端点上，对应地查找 $10$ 个值即可。这个需要用到区间加，单点查，减小常数可以使用树状数组。

本题的一大难点在于你分析出时间复杂度是 $Θ (10 (n + m) \log n)$ 还要相信这个东西能过。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n,m,a[N],pos[N],ans[11][N],vis[N];
vector <pair <int,int> > q[N];
vector <pair <int,int> > np;
inline int read()
{
    int s = 0; char k = getchar();
    while(!isdigit(k)) k = getchar();
    while(isdigit(k)) s = (s << 3) + (s << 1) + (k ^ 48),k = getchar();
    return s;
}
struct BIT{
    int b[N];
    inline int lowbit(int x) {return x & (-x);}
    inline void modify(int x,int k) {for(;x <= n;x += lowbit(x)) b[x] += k;}
    inline int query(int x) {int ret = 0; for(;x;x -= lowbit(x)) ret += b[x]; return ret;}
    inline void md(int l,int r,int k) {modify(l,k); modify(r + 1,-k);}
}t[12];
int main()
{
    n = read(); m = read();
    for(int i = 1;i <= n;i++) a[i] = read();
    for(int i = 1,x,y;i <= m;i++)
    {
        x = read(); y = read();
        q[y].push_back(make_pair(x,i));
    }
    for(int i = 1;i <= n;i++)
    {
        np.clear();
        for(int j = max(1,a[i] - 11);j <= min(n,a[i] + 11);j++) 
            if(pos[j] > pos[a[i]])
                np.push_back(make_pair(pos[j],j));
        sort(np.begin(),np.end(),[&](pair <int,int> x,pair <int,int> y) {return x.first > y.first;});
        int tmp = i,nl = a[i],nr = a[i];
        for(auto in : np)
        {
            if(nl < a[i]) t[a[i] - nl].md(in.first + 1,tmp,-1);
            if(nr > a[i]) t[nr - a[i]].md(in.first + 1,tmp,-1);
            if(nr - nl + 1 <= 11) t[a[i] - nl + nr - a[i] + 1].md(in.first + 1,tmp,1);
            vis[in.second] = 1;
            while(vis[nl - 1] > 0) nl--;
            while(vis[nr + 1] > 0) nr++;
            tmp = in.first;
        }
        for(auto in : np) vis[in.second] = 0;
        if(nl < a[i]) t[a[i] - nl].md(pos[a[i]] + 1,tmp,-1);
        if(nr > a[i]) t[nr - a[i]].md(pos[a[i]] + 1,tmp,-1);
        if(nr - nl + 1 <= 11) t[a[i] - nl + nr - a[i] + 1].md(pos[a[i]] + 1,tmp,1);
        for(auto in : q[i])
            for(int j = 1;j <= 10;j++) 
                ans[j][in.second] = t[j].query(in.first);
        pos[a[i]] = i;
    }
    for(int i = 1;i <= m;i++,putchar('\n'))
        for(int j = 1;j <= 10;j++)
            printf("%d",ans[j][i] % 10);
    return 0;
}

特殊的扫描方法

虽然没有例题，顺带提一句，扫描线可以很特殊地做。

比如说有时我们会遇到一些难以撤销的操作（像是维护单调栈），这时如果再扫时间，维护序列的状态就不太可做。

我们发现，其实时间和序列相当于两维，所以我们可以换过来扫。

我们扫描序列的每一位，DS 上维护每一个时间节点这个位置的值，这样做的依据是序列操作通常是区间操作，上一个位置和这个位置很多修改是重叠的，可以通过 $Θ (m)$ 次线段树上操作来维护，如果是单点查信息的话，直接对应位置问时间节点即可。

这样还可以统计 “某个位置在过去的 $[l, r]$ 时间里” 这样的信息。

区间历史和

和之前一样，最关键的东西就是在于分析 “历史版本更新” 标记和其他标记怎么 $Θ (1)$ 合并。

例如 lxl 上课讲的区间乘，假如现在有一个标记序列：

乘 $a$ 、乘 $b$ 、历史加、历史加、乘 $c$ 、历史加

首先合并同类项：

乘 $a b$ 、历史加 $\times 2$ 、乘 $c$ 、历史加

我们主要考虑前面的乘对后面历史加的影响，发现乘 $x$ 后再加入历史可以看作加入历史 $x$ 次，所以这个序列被拍扁了，成为：

乘法标记： $a b c$

历史标记： $2 a b + a b c$

相应的历史标记在打的时候调用当时的乘法标记即可。

再例如区间加，假如现在有一个标记序列：

加 $a$ 、历史加、加 $c$ 、历史加

考虑历史版本也被额外加了一些值，我们再维护一个 $δ$ ，代表历史和额外加上了多少，观察得到上面的 $δ = 2 a + c$ 。

考虑父亲的 lazytag 向儿子合并的过程：

父亲：加法标记 $a$ ，历史标记 $b$ ，历史和额外加 $c$ 。

儿子：加法标记 $d$ ，历史标记 $e$ ，历史和额外加 $f$ 。

儿子：加法标记 $a + d$ ，历史标记 $b + e$ 是显然的。

我们考虑 $b$ 对儿子的历史和的影响，发现儿子加的 $d$ 被多贡献了 $b$ 次，儿子新的历史和额外标记就是 $c + f + b d$ 。

（有没有像 cdq 分治？）

对儿子值的影响：

$h i s + = s u m^{'} \times b + (c + b d) \times (r - l + 1)$ 。

考虑 $s u m^{'}$ 是原来的 $s u m$ ，首先多加了 $b$ 遍，然后要考虑历史和额外的影响，发现历史和比原来多了 $(c + b d)$ ，所以区间上就要加 $(c + b d) \times (r - l + 1)$ 。

$s u m + = a \times (r - l + 1)$ （显然）

这样，一个节点维护 $a, b, c, h i s, s u m$ 五个值就可以完成了。

分块与莫队

莫队的本质

莫队本质上是一种用 $Θ (n \sqrt{n})$ 的代价去掉问题的两维限制的一种高效算法。（不要看不起根号，这个效率已经很高了）。

比如说，现在询问区间 $[l, r]$ 中，值域在 $[x, y]$ 中的数有多少个。

四维统计十分困难，所以我们可以用莫队除掉两维，假设去掉 $[l, r]$ ，我们通过指针的移动得到区间 $[l, r]$ 的信息，转化为全局问题：

支持插入，删除数字，求 $[x, y]$ 中的有多少个。

可以用 BIT 做，时间复杂度 $Θ (\log n)$ 。总复杂度 $Θ (n \sqrt{n} \log n)$ 。

太多了？考虑到莫队的移动是 $Θ (n \sqrt{n})$ ，但询问是 $Θ (n)$ 次。所以考虑平衡，我们需要一个 $Θ (\sqrt{n})$ 询问， $Θ (1)$ 修改的结构，值域分块即可。

这样，我们就做到了 $Θ (n \sqrt{n})$ 。

如果我们把两端点 $[l, r]$ 看作一个点的话，那么莫队就可以看作一个坐标系内 $m$ 个点的较短的哈密尔顿回路。用大约 $Θ (n \sqrt{m})$ 的路程遍历完了 $m$ 的路程。

至此来看，莫队不仅限于一个区间的问题，而是将一个集合序列 $S_{1}, S_{2}, \dots S_{m}$ 排序，使得相邻两项的对称差尽量小的一个问题。

莫队 “尾巴” 复杂度的优化

通常我们发现，在比较复杂的问题当中，莫队的指针无法做到 $Θ (1)$ 移动，例如上题就是 $Θ (\log n)$ 的。

这种题一般有调整数据结构或者二次离线两种做法。

二次离线自行百度。

P4396 [AHOI2013] 作业

类似，值域分块即可。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
struct Q{
    int l,r,a,b,pos;
    pair <int,int> ans;
}q[N];
int n,m,B,a[N];
inline int kuai(int x) {return (x - 1) / B + 1;}
struct Part{
    int pot[N],potK[N],num[N],numK[N];
    inline int st(int x) {return (x - 1) * B + 1;}
    inline int ed(int x) {return x * B;}
    inline void ist(int x)
    {
        if(!pot[x]) num[x]++,numK[kuai(x)]++;
        pot[x]++,potK[kuai(x)]++; 
    }
    inline void del(int x)
    {
        pot[x]--,potK[kuai(x)]--;
        if(!pot[x]) num[x]--,numK[kuai(x)]--;
    }
    inline pair <int,int> query(int l,int r)
    {
        pair <int,int> ret = make_pair(0,0);
        if(kuai(l) == kuai(r))
        {
            for(int i = l;i <= r;i++) ret.first += pot[i],ret.second += num[i];
            return ret;
        }    
        for(int i = l;i <= ed(kuai(l));i++) ret.first += pot[i],ret.second += num[i];
        for(int i = kuai(l) + 1;i <= kuai(r) - 1;i++) ret.first += potK[i],ret.second += numK[i];
        for(int i = st(kuai(r));i <= r;i++) ret.first += pot[i],ret.second += num[i];
        return ret;
    }
}t;
int main()
{
    cin>>n>>m;
    B = sqrt(n);
    for(int i = 1;i <= n;i++) cin>>a[i];
    for(int i = 1;i <= m;i++) cin>>q[i].l>>q[i].r>>q[i].a>>q[i].b,q[i].pos = i;
    sort(q + 1,q + m + 1,[&](Q x,Q y) {return (kuai(x.l) ^ kuai(y.l)) ? kuai(x.l) < kuai(y.l) : x.r < y.r;});
    for(int i = 1,nl = 1,nr = 0;i <= m;i++)
    {
        while(nr < q[i].r) {++nr; t.ist(a[nr]);}
        while(nl > q[i].l) {--nl; t.ist(a[nl]);}
        while(nr > q[i].r) {t.del(a[nr]); --nr;}
        while(nl < q[i].l) {t.del(a[nl]); ++nl;}
        q[i].ans = t.query(q[i].a,q[i].b);
    }
    sort(q + 1,q + m + 1,[&](Q x,Q y) {return x.pos < y.pos;});
    for(int i = 1;i <= m;i++) cout<<q[i].ans.first<<" "<<q[i].ans.second<< '\n';
    return 0;
}

P5386 [Cnoi2019] 数字游戏

这题我们考虑扫下标很困难，所以我们扫描值域，将当前值域固定在 $[x, y]$ 上，中间值对应的位置赋为 $1$ ，其余的赋为 $0$ 。我们要求的值和极长 $1$ 连续段的平方有关。

可以用回滚莫队 + 带撤销并查集解决，但是带撤销并查集有 $Θ (\log n)$ 的时间，所以我们考虑用 $Θ (1)$ 代替，记录一个连续段右端点对应的左端，和左端对应的右端，得到长度。

~~事实上这个写着很麻烦，并查集貌似可以过。~~

莫队模型的转化

莫队由于是区间统计信息，经常可以用差分将自由度降低，简化问题。

P4689 [Ynoi2016] 这是我自己的发明

考虑子树可以用 dfn 序转化为区间，考虑以一个随机点为根建树，讨论 $x$ 和 $r o o t$ 的位置关系：

如果 $r o o t$ 在 $x$ 的子树外，那么 $x$ 对应的就是原来的子树。
如果 $r o o t$ 在 $x$ 的子树内，假设 $v$ 是 $x$ 在 $r o o t$ 方向的儿子，那么 $x$ 对应的就是整棵树除了 $v$ 以外的部分。

所以 $x, y$ 顶多对应 $2$ 个区间， $x$ 的区间和 $y$ 的两两对应，加起来就是答案。

我们考虑两个区间各选一个点的答案，设为 $f (a, b, c, d)$ ，区间为 $[a, b], [c, d]$ 。

我们发现 “对面的区间与自己相同的数字个数” 这个信息是可以差分的，所以：

f (a, b, c, d) = f (1, b, c, d) - f (1, a - 1, c, d)

= f (1, b, 1, d) - f (1, a - 1, 1, d) - f (1, b, 1, c - 1) + f (1, a - 1, 1, c - 1)

对于两个前缀，直接双指针，移动指针的时候答案加/减对面区间与这一位相同的数字个数就好了。

这样，我们就将一个询问转化为了 16 个区间问题。

题解区有 9 和 4 个的转化方式，本质相同，自行阅读。

至于 $16 \times 5 e 5$ 次莫队为什么能过，貌似是因为这道题使用莫队的 “哈密尔顿回路” 很短？

#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
typedef long long ll;
struct Query1{
    vector <pair <int,int> > A,B;
    vector <int> addans;
}q1[N];
struct Query2{
    int a,b,c,d;
    ll ans;
    vector <int> add,minu;
}q2[N * 4];
struct Query3{
    int l,r,pos;
    ll ans;
}q3[N * 16];
int n,m,a[N],tot = 0,fa[21][N],dep[N],nowroot = 1,dfn[N],siz[N],cnt1 = 0,cnt2 = 0;
int potA[N],potB[N],B;
vector <int> G[N];
inline int read()
{
    int s = 0; char k = getchar();
    while(!isdigit(k)) k = getchar();
    while(isdigit(k)) {s = (s << 3) + (s << 1) + (k ^ 48); k = getchar();}
    return s;
}
inline void dfs(int x,int last)
{
    dfn[x] = ++tot;
    siz[x] = 1;
    dep[x] = dep[last] + 1;
    fa[0][x] = last;
    for(auto to : G[x])
    {
        if(to == last) continue;
        dfs(to,x);
        siz[x] += siz[to];
    }
}
inline int jump(int x,int dep)
{
    for(int i = 17;i >= 0;i--) if(dep >= (1 << i)) dep -= (1 << i),x = fa[i][x];
    return x;
}
inline int kuai(int x) {return (x - 1) / B + 1;}
int main() 
{
    n = read(); m = read();
    for(int i = 1;i <= n;i++) a[i] = read();
    for(int i = 1,x,y;i <= n - 1;i++)
    {
        x = read(); y = read();
        G[x].push_back(y);
        G[y].push_back(x); 
    } 
    dfs(nowroot,0);
    for(int i = 1;i <= 17;i++)
        for(int j = 1;j <= n;j++)
            fa[i][j] = fa[i - 1][fa[i - 1][j]];
    static int val[N],nowcnt = 0;
    for(int i = 1;i <= n;i++) val[++nowcnt] = a[i];
    sort(val + 1,val + nowcnt + 1);
    nowcnt = unique(val + 1,val + nowcnt + 1) - (val + 1);
    for(int i = 1;i <= n;i++) a[i] = lower_bound(val + 1,val + nowcnt + 1,a[i]) - val;
    for(int i = 1;i <= n;i++) val[dfn[i]] = a[i];
    for(int i = 1;i <= n;i++) a[i] = val[i];
    for(int i = 1,op,x,y;i <= m;i++)
    {
        op = read();
        if(op == 1)
        {
            x = read(); 
            nowroot = x;
        }
        else
        {
            x = read(); y = read();
            if(dep[x] < dep[nowroot])
            {
                if(jump(nowroot,dep[nowroot] - dep[x]) == x)
                {
                    int now = jump(nowroot,dep[nowroot] - dep[x] - 1);
                    if(dfn[now] > 1) q1[i].A.push_back(make_pair(1,dfn[now] - 1));
                    if(dfn[now] + siz[now] <= n) q1[i].A.push_back(make_pair(dfn[now] + siz[now],n));
                }
                else q1[i].A.push_back(make_pair(dfn[x],dfn[x] + siz[x] - 1));
            }
            else if(x == nowroot) q1[i].A.push_back(make_pair(1,n));
            else q1[i].A.push_back(make_pair(dfn[x],dfn[x] + siz[x] - 1));

            if(dep[y] < dep[nowroot])
            {
                if(jump(nowroot,dep[nowroot] - dep[y]) == y)
                {
                    int now = jump(nowroot,dep[nowroot] - dep[y] - 1);
                    if(dfn[now] > 1) q1[i].B.push_back(make_pair(1,dfn[now] - 1));
                    if(dfn[now] + siz[now] <= n) q1[i].B.push_back(make_pair(dfn[now] + siz[now],n));
                }
                else q1[i].B.push_back(make_pair(dfn[y],dfn[y] + siz[y] - 1));
            }
            else if(y == nowroot) q1[i].B.push_back(make_pair(1,n));
            else q1[i].B.push_back(make_pair(dfn[y],dfn[y] + siz[y] - 1));
        }
    }
    for(int i = 1;i <= m;i++)
    {
        if(q1[i].A.empty()) continue;
        for(auto in : q1[i].A)
            for(auto to : q1[i].B)
            {
                ++cnt1;
                q2[cnt1].a = in.first,q2[cnt1].b = in.second,q2[cnt1].c = to.first,q2[cnt1].d = to.second;
                q1[i].addans.push_back(cnt1); 
            }
    }
    for(int i = 1;i <= cnt1;i++)
    {
        ++cnt2;
        q3[cnt2].pos = cnt2; q3[cnt2].l = q2[i].b; q3[cnt2].r = q2[i].d; q2[i].add.push_back(cnt2); 
        ++cnt2;
        q3[cnt2].pos = cnt2; q3[cnt2].l = q2[i].a - 1; q3[cnt2].r = q2[i].d; q2[i].minu.push_back(cnt2);
        ++cnt2;
        q3[cnt2].pos = cnt2; q3[cnt2].l = q2[i].b; q3[cnt2].r = q2[i].c - 1; q2[i].minu.push_back(cnt2);
        ++cnt2;
        q3[cnt2].pos = cnt2; q3[cnt2].l = q2[i].a - 1; q3[cnt2].r = q2[i].c - 1; q2[i].add.push_back(cnt2);
    }
    if(n < sqrt(cnt2)) B = sqrt(n);
    else B = (int)(n / sqrt(cnt2));
    for(int i = 1;i <= cnt2;i++)
    {
        int x = q3[i].l,y = q3[i].r;
        q3[i].l = min(x,y);
        q3[i].r = max(x,y);
    }
    sort(q3 + 1,q3 + cnt2 + 1,[&](Query3 x,Query3 y) {return (kuai(x.l) ^ kuai(y.l)) ? (kuai(x.l) < kuai(y.l)) : ((kuai(x.l) & 1) ? x.r < y.r : x.r > y.r);});
    ll nowans = 0;
    for(int i = 1,nl = 0,nr = 0;i <= cnt2;i++)
    {
        if(q3[i].l == 0 || q3[i].r == 0) {q3[i].ans = 0; continue;}
        while(nr < q3[i].r) {++nr; nowans += potA[a[nr]]; potB[a[nr]]++;}
        while(nl > q3[i].l) {nowans -= potB[a[nl]]; potA[a[nl]]--; --nl;}
        while(nr > q3[i].r) {nowans -= potA[a[nr]]; potB[a[nr]]--; --nr;}
        while(nl < q3[i].l) {++nl; nowans += potB[a[nl]]; potA[a[nl]]++;}
        q3[i].ans = nowans;
    }
    sort(q3 + 1,q3 + cnt2 + 1,[&](Query3 x,Query3 y) {return x.pos < y.pos;});
    for(int i = 1;i <= cnt1;i++) 
    {
        q2[i].ans = 0;
        for(auto in : q2[i].add) q2[i].ans += q3[in].ans;
        for(auto in : q2[i].minu) q2[i].ans -= q3[in].ans;
    }
    for(int i = 1;i <= m;i++)
    {
        if(q1[i].A.empty()) continue;
        ll res = 0;
        for(auto in : q1[i].addans) res += q2[in].ans;
        cout<<res<< '\n';
    }
    return 0;
}

P3245 [HNOI2016] 大数

探究 $[l, r]$ 整除的条件，容易想到模数为 $0$ 。假设 $s_{i}$ 为 $[i, n]$ 组成的数字，则：

\frac{s_{l} - s_{r + 1}}{10^{r - l + 1}} \equiv 0 \mod p

分类讨论，如果 $p \neq 2, p \neq 5$ ，那么 $gcd (10, p) = 1$ ，所以 $10^{r - l + 1}$ 一定有逆元。

所以 $s_{l} - s_{r + 1} \equiv 0 \mod p$ 。

所以算出取模结果后移动指针加上桶的个数（相同数字的个数）即可。

如果 $p = 2$ ，整除的充要条件就是最后一位为偶数，这个可以直接莫队计算。

如果 $p = 5$ ，整除的充要条件就是最后一位为 $5, 0$ ，同理。

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
int n,p,m,B,sum[N],a[N],b[N],pw[N];
typedef long long ll;
struct Q{
    int l,r,pos;
    ll ans;
}q[N];
string s;
inline void spe()
{
    ll nowans = 0;
    for(int i = 1,nl = 1,nr = 0,num = 0;i <= m;i++)
    {
        while(nr < q[i].r) 
        {
            ++nr;
            if(p == 2 && a[nr] % 2 == 0) nowans += nr - nl + 1,num++;
            if(p == 5 && a[nr] % 5 == 0) nowans += nr - nl + 1,num++;
        }
        while(nl > q[i].l)
        {
            --nl;
            if(p == 2 && a[nl] % 2 == 0) num++;
            if(p == 5 && a[nl] % 5 == 0) num++;
            nowans += num; 
        }
        while(nr > q[i].r)
        {
            if(p == 2 && a[nr] % 2 == 0) nowans -= nr - nl + 1,num--;
            if(p == 5 && a[nr] % 5 == 0) nowans -= nr - nl + 1,num--;
            nr--;
        }
        while(nl < q[i].l)
        {
            nowans -= num;
            if(p == 2 && a[nl] % 2 == 0) num--;
            if(p == 5 && a[nl] % 5 == 0) num--;
            nl++;
        }
        q[i].ans = nowans;
    }
}
inline int ksm(int base,int pts)
{
    int ret = 1;
    for(;pts > 0;pts >>= 1,base = 1ll * base * base % p)
        if(pts & 1)
            ret = 1ll * ret * base % p;
    return ret;
}
inline void solve()
{
    static int val[N],cnt = 0,pot[N];
    for(int i = 1;i <= n + 1;i++) val[++cnt] = sum[i];
    sort(val + 1,val + cnt + 1);
    cnt = unique(val + 1,val + cnt + 1) - (val + 1);
    for(int i = 1;i <= n + 1;i++) sum[i] = lower_bound(val + 1,val + cnt + 1,sum[i]) - val;
    ll nowans = 0; pot[sum[1]]++;
    for(int i = 1,nl = 1,nr = 0;i <= m;i++)
    {
        while(nr < q[i].r) {++nr; nowans += pot[sum[nr + 1]]; pot[sum[nr + 1]]++;}
        while(nl > q[i].l) {--nl; nowans += pot[sum[nl]]; pot[sum[nl]]++;}
        while(nr > q[i].r) {pot[sum[nr + 1]]--; nowans -= pot[sum[nr + 1]]; nr--;}
        while(nl < q[i].l) {pot[sum[nl]]--; nowans -= pot[sum[nl]]; nl++;}
        q[i].ans = nowans;
    }
}
inline int kuai(int x) {return (x - 1) / B + 1;}
int main()
{
    cin>>p;
    cin>>s;
    n = s.length();
    B = sqrt(n);
    pw[0] = 1;
    for(int i = 1;i <= n;i++) pw[i] = 1ll * pw[i - 1] * 10 % p;
    for(int i = 0;i < n;i++) a[i + 1] = (s[i] - '0');
    cin>>m;
    for(int i = 1;i <= m;i++)
    {
        cin>>q[i].l>>q[i].r;
        q[i].pos = i;
    }
    for(int i = n;i >= 1;i--) sum[i] = (sum[i + 1] + 1ll * a[i] * pw[n - i] % p) % p;
    sort(q + 1,q + m + 1,[&](Q x,Q y) {return (kuai(x.l) ^ kuai(y.l)) ? (kuai(x.l) < kuai(y.l)) : (x.r < y.r);});
    if(p == 2 || p == 5) spe(); 
    else solve();
    sort(q + 1,q + m + 1,[&](Q x,Q y) {return x.pos < y.pos;});
    for(int i = 1;i <= m;i++) cout<<q[i].ans<< '\n';
    return 0;
}

可持久化数据结构

我们考虑扫描线的过程，我们因为需要知道扫描线扫到中间某个点的时候，当前数据结构（例如线段树）的状态，所以我们离线询问做这个问题，动态做扫描线。

那么，我们可不可以 “离线这个扫描线”，达到动态回答询问的效果呢？答案显然是可以，就是这个可持久化的数据结构，考虑到修改单点的次数总共是 $Θ (n)$ 的，所以我们每次从上一个版本继承大部分的信息，只新开一些节点存储当前的信息。

这个方法叫做 “Path Copy” ，已经可以解决绝大多数的可持久化问题。

可持久化 01 trie

「2017 山东三轮集训 Day6」C

考虑 01 trie 可以解决 “全局异或 $x$ 后的第 $k$ 大” 这个问题，我们对序列做可持久化之后就可以通过差分得到区间的信息。解决 “区间异或 $x$ 后的第 $k$ 大” 这样的问题。

所以对于本题的异或操作，我们直接对于每一个二进制位打一个翻转标记，查第 $k$ 小时直接异或上这一位再贪心选择即可。

但是我们发现，trie 树上或 + 与等于将某一位的所有 $0 / 1$ 子树和另外一个并起来，这个不好解决，但是我们发现，全局做了一次操作以后，当前位就会变得一样，后面的与/或操作可以看成这一位上面的异或操作。

所以 “真正的” 与 + 或操作不会超过 $Θ (\log V)$ 次。

复杂度有保证就好做了，直接暴力重构 01 trie 即可，时间复杂度 $Θ (n \log^{2} V)$ ，注意回收空间，不要傻乎乎地开 $Θ (n \log^{2} V)$ 的空间。

~~没写，代码咕。~~

主席树

Listening to Music

这种题目的套路是，考虑 $x$ 的取值范围被每个 $a_{i}$ 分成了 $a_{i} + 1$ 段，每一段面临的局面都是一样的，所以我们考虑在线作答，就建出这些局面的主席树，每次在主席树上区间修改，区间查询最小值。

这里对于主席树，不好 pushdown，所以我们考虑标记永久化，记录节点的 $v a l, t a g$ ，更新：

v a l = min (v a l_{l c}, v a l_{r c}) + t a g

所以我们就做完了。

MLE ？？？一看发现这题空限 64 MB ，卡死主席树，于是我们玩点骚操作：

考虑值，值最多是 $n$ ， $\leq 2^{17}$ 。
线段树左右儿子下标，考虑一个 unsigned long long ，减去 18 位还剩 46 位，左右儿子各分 23 位，可以达到 $8 \times 10^{6}$ ，假设足够。

所以，我们用 “位域” 这个神秘的东西压下了三个信息，这样可以支持开 $2 e 5 \times 40$ 个节点。

但是还有一个标记，这里我们考虑将 $x$ 从大到小排序，维护 “大于等于 $x$ 的数有多少个”，取最大值然后取 $max$ （因为取 $min$ 这里会出现神秘 WA，猜测可能是因为加法标记是正数的原因）。

然后我们不记录这个标记，每次区间被包含就将 $v a l + +$ ，向下递归前可以得到这个点的 $t a g = v a l - max (v a l_{l c}, v a l_{r c})$ 。这样就还原了 $t a g$ 信息。

考虑这样仍然不够，会 RE，我们想到一个小优化：叶节点不需要新开节点，一旦递归到叶节点，那么情况只有一种，举例子：如果当前点 $p o s$ 的 $l c$ 是叶节点 $(l = r)$ ，那么直接将 $l c$ 记为这个值，假设我们基于前面的 $p o s y$ ，那么 $p o s y$ 也是这样构成的，所以直接 $p o s = p o s y + 1$ 即可，查询的时候特判。

这样相当于削掉了底层的节点，看似不多，恰好够卡过这道题。

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5;
bool st;
struct Node{
	unsigned long long v : 18,lc : 23,rc : 23;
}t[N * 40];
int tot = 0;
inline int getv(int l,int r,int x) {return (l == r) ? x : t[x].v;}
inline int modify(int l,int r,int L,int R,int posy)
{
	if(l == r) 	return posy + 1;
	int pos = ++tot; t[pos] = t[posy];
	if(L <= l && r <= R) {t[pos].v++; return pos;}
	int mid = (l + r) >> 1,tg = t[pos].v - max(getv(l,mid,t[pos].lc),getv(mid + 1,r,t[pos].rc));
	if(L <= mid) t[pos].lc = modify(l,mid,L,R,t[posy].lc);
	if(R > mid) t[pos].rc = modify(mid + 1,r,L,R,t[posy].rc);
	t[pos].v = max(getv(l,mid,t[pos].lc),getv(mid + 1,r,t[pos].rc)) + tg; 
	return pos;
}
inline int query(int l,int r,int L,int R,int pos)
{
	if(l == r) return pos; 
	if(!pos) return 0;
	if(L <= l && r <= R) return (int)t[pos].v;
	int mid = (l + r) >> 1,ret = 0;
	if(L <= mid) ret = max(ret,query(l,mid,L,R,t[pos].lc));
	if(R > mid) ret = max(ret,query(mid + 1,r,L,R,t[pos].rc));
	ret += t[pos].v - max(getv(l,mid,t[pos].lc),getv(mid + 1,r,t[pos].rc));
	return ret;
}
int n,m,s,B,val[N],root[N],cnt = 0,a[N];
inline int fd(int x)
{
	int l = 0,r = n;
	while(l < r)
	{
		int mid = (l + r + 1) >> 1;
		if(val[a[mid]] >= x) l = mid;
		else r = mid - 1;
	}
	return l;
}
bool ed;
inline int read()
{
	int s = 0; char k = getchar();
	while(!isdigit(k)) k = getchar();
	while(isdigit(k)) s = (s << 3) + (s << 1) + (k ^ 48),k = getchar();
	return s;
}
int main()
{
	n = read(); m = read(); B = n - m + 1;
	for(int i = 1,x;i <= n;i++) x = read(),a[i] = x;
	for(int i = 1;i <= n;i++) val[++cnt] = a[i],a[i] = i;
	sort(a + 1,a + n + 1,[&](int x,int y) {return val[x] > val[y];});
	tot = 0;
	for(int i = 1;i <= n;i++) 
		root[i] = modify(1,B,max(1,a[i] - m + 1),min(B,a[i]),root[i - 1]);
	s = read();
	int lastans = 0;
	for(int i = 1,l,r,x;i <= s;i++)
	{
		l = read(); r = read(); x = read();
		x ^= lastans;
		x = fd(x);
		lastans = m - query(1,B,l,r,root[x]);
		printf("%d\n",lastans);
	}
	return 0;
}

posted @ 2023-11-23 21:24 The_Last_Candy 阅读(195) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 【数据结构】线段树解决历史问题

· 【数据结构】吉司机线段树

· 莫队算法学习笔记

· 莫队学习笔记

· 莫队算法学习笔记

阅读排行：
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 单线程的Redis速度为什么快？
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决：字节Trae VS Cursor，谁才是开发者新宠？
· 展开说说关于C#中ORM框架的用法！

公告

友链

jeefy
hfjh
cyantist
ricky_lin
神犇Smallbasic

昵称： The_Last_Candy
园龄： 2年1个月
粉丝： 6
关注： 6

+加关注

2025年3月

日

一

二

三

四

五

六

The_Last_Candy

【数据结构】lxl 的 DS 修炼

【数据结构】lxl 的 DS 修炼

线段树 & 平衡树

技巧

ODT/颜色段均摊

扫描线

特殊的扫描方法

区间历史和

分块与莫队

莫队的本质

莫队 “尾巴” 复杂度的优化

莫队模型的转化

可持久化数据结构

可持久化 01 trie

主席树

公告

友链

搜索

常用链接

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论