【图论】一般图最大匹配

题目描述

给出一张 \(n\) 个点和 \(m\) 条边的无向图，求最大匹配数及方案。

\(2 \leq n \leq 10^3,1 \leq m \leq 5 \times 10^4\) 。

算法概述

带花树算法，在基于 bfs 版本的匈牙利上改造。考虑一般的二分图，它的特征是出现环的情况下只有偶环。然而一般的图里面可能有奇环，找匹配点不只可以找同侧点，所以不能用匈牙利。

我们将一个图二分图染色，如果是黑色，就找白色或者未染色出边，匹配那个点，然后将那个点的 \(match_{v}\) 拿去和其他点匹配。所以记这个黑点和“预选”的白点之间的连接为 \(pre\) 指针，每次 \(pre_v = u\) ，然而一个黑点向上一个，就是原本匹配的白点（现在可能要换）的连边就是 \(match\) ，连边就像这样：

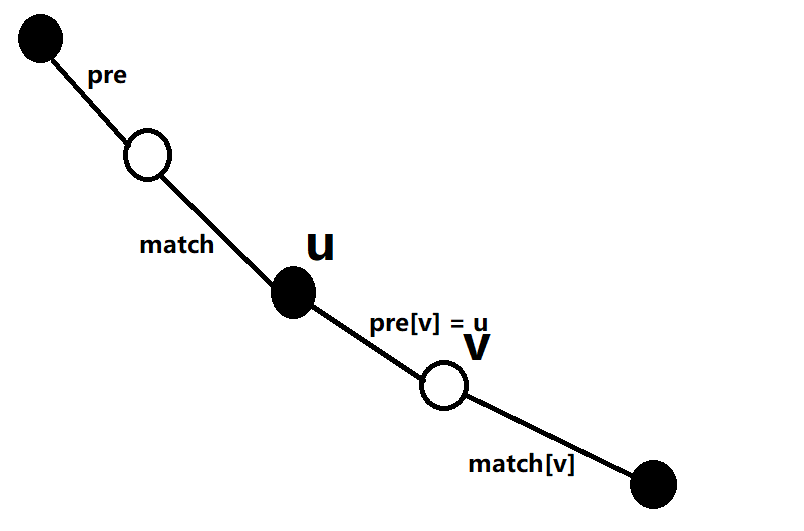
注意队列里只有黑点，没有白点。

这里，我们只需要考虑黑点向黑点连边的情况，我们发现现在连成了一个奇环。环上一定是 \(pre\) 边和 \(match\) 边交替的情况，考虑这个奇环可以缩点在一起，当作同一个点向外匹配，由于内部的交错情况是不确定的，所以要将所有点的状态都置为黑点，所有边都连上 \(pre\) 标记。

考虑并查集完成这一过程，首先找到两个点在搜索路径上的 \(lca\) （花根）。然后从两个方向依次向上跳。跳跃过程中暂时保存节点的匹配情况，也就是 \(match\) 值不变，改变每个点的颜色为黑色，并且并查集缩在一起，就可以完成合并。

至于去找这个花根，从两个点开始交错向上跳，跳过的黑点打标记，如果跳到了一个标记相同的点，一定是花根。

然后如果找到了没匹配的点的话，就直接通过 \(pre\) 和 \(match\) 标记遍历回起点，路上将增广路取反即可。（这里求增广路这个过程就更加形象了）

这个算法主要麻烦的一点就是连边不是单纯的通过 \(match\) 连，而是 \(match\) 和 \(pre\) 交替连边，所以跳的时候有点麻烦，细节见代码。

时间复杂度和匈牙利一样，是 \(\Theta(n^3)\) 。

Code

#include<bits/stdc++.h>
using namespace std;
const int N = 1005,M = 5e4 + 5;
struct Edge{
	int v,next;
}e[M * 2];
int vis[N],match[N],mark[N],head[N],pre[N],n,m,tot = 0;
inline void add(int x,int y)
{
	++tot;
	e[tot].v = y;
	e[tot].next = head[x];
	head[x] = tot;
}
queue <int> q;
int fa[N];
inline int find(int x)
{
	if(x == fa[x]) return x;
	return find(fa[x]);
}
inline int getlca(int x,int y)
{
	++tot;
	x = find(x); y = find(y);
	while(mark[x] != tot)
	{
		mark[x] = tot;
		x = find(pre[match[x]]);
		if(y) swap(x,y);
	} 
	return x;
}
inline void blossom(int x,int y,int z)
{
	while(find(x) != z)
	{
		pre[x] = y;
		y = match[x];
		if(vis[y] != 1) vis[y] = 1,q.push(y);
		if(find(x) == x) fa[x] = z;
		if(find(y) == y) fa[y] = z;
		x = pre[y];		
	}
}
inline bool try_match(int st)
{
	for(int i = 1;i <= n;i++) fa[i] = i;
	memset(vis,0,sizeof(vis)); memset(pre,0,sizeof(pre));
	while(!q.empty()) q.pop();
	q.push(st);
	vis[st] = 1;
	while(!q.empty())
	{
		int x = q.front(); q.pop();
		for(int i = head[x];i;i = e[i].next)
		{
			int to = e[i].v;
			if(find(x) == find(to)) continue; // in the same flower
			if(vis[to] == 2) continue; //even circle
			if(!vis[to]) 
			{
				pre[to] = x; vis[to] = 2;
				if(!match[to])
				{
					for(int j = to,k;j;j = k)
					{
						k = match[pre[j]];
						match[j] = pre[j];
						match[pre[j]] = j;
					}
					return true;
				}
				else q.push(match[to]),vis[match[to]] = 1;
			}
			else
			{
				int z = getlca(x,to);
				blossom(x,to,z);
				blossom(to,x,z); 
			}
		}
	}	
	return 0;
}
int main()
{
	cin>>n>>m;
	for(int i = 1,x,y;i <= m;i++) cin>>x>>y,add(x,y),add(y,x);
	int ans = 0; tot = 0;
	for(int i = 1;i <= n;i++) if(!match[i]) ans += try_match(i); 
	cout<<ans<<endl;
	for(int i = 1;i <= n;i++) cout<<match[i]<<" ";
	return 0;
}