【枚举】【贪心技巧】【集训队互测2021】子集匹配

题目描述

给定 \(n,k(2k \geq n)\) ，二进制中有 \(k\) 个 \(1\) 的不超过 \(n\) 位的数有 \(\binom{n}{k}\) 个，有 \(k - 1\) 个 \(1\) 的有 \(\binom n{k - 1}\) 个，后者显然大于等于前者，要求对于每一个 \(k\) 个 \(1\) 的数 \(x\)，都找出一个 \(k - 1\) 位的数 \(y\) 与之对应，且 \(x \& y = y\)，每一个 \(y\) 只能对应一个 \(x\) 。

\(1 \leq k \leq n \leq 27\) 。

算法概述

这道题要求我们 \(O(1)\) 地将一个集合映射到一个集合上且不重不漏，考虑一种神秘的构造方法：从小到大枚举每一个要进行映射的数，从高到低枚举每一位 \(1\) ，去掉这一位形成一个新的数 \(y\) ，如果 \(y\) 没有用过就对应 \(y\) 。

感性理解，就是前面的数很小，后面的数很大，我们优先去掉高位，让占用的数尽量小，更少地影响到后面的大数，一定能分配好。

这样做要用一个 \(bitset\) 维护，空间 \(\Theta(\frac nw)\) ，如果我们需要 \(O(1)\) 的空间呢？

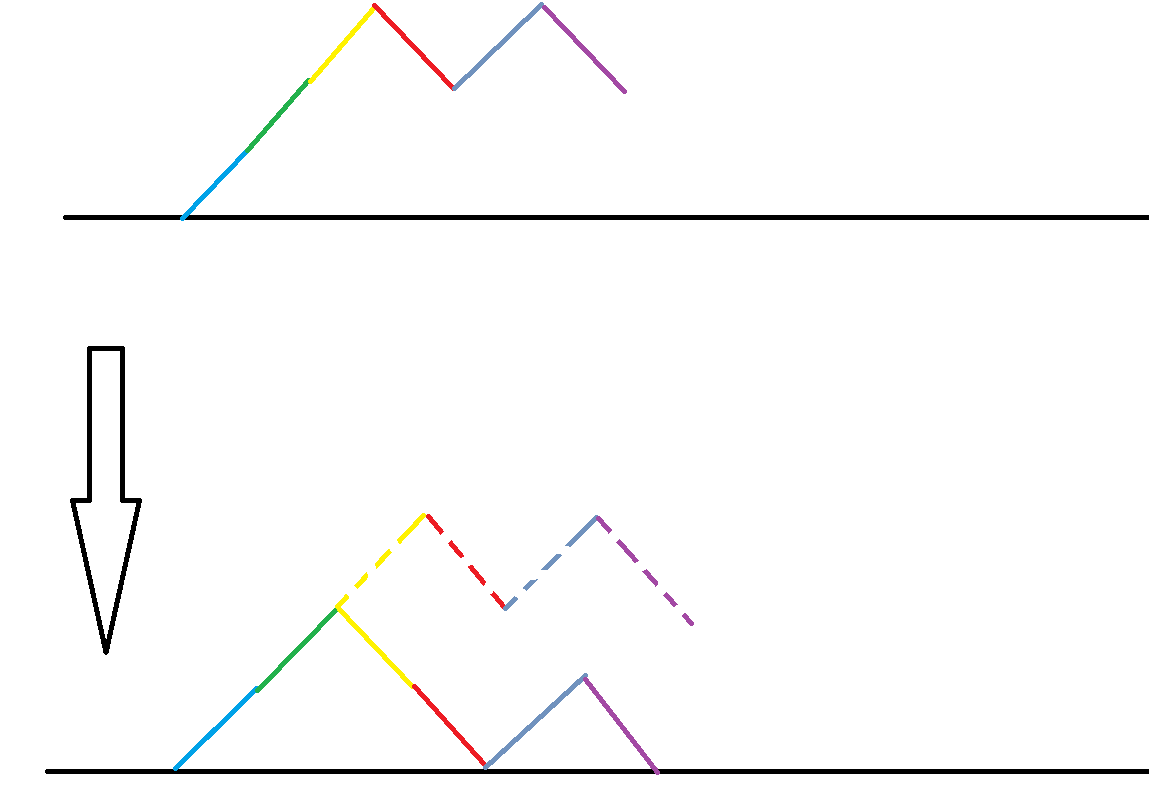
我们将二进制从低到高看作一个折线图，\(1\) 为 \(+1\) ，\(0\) 为 \(-1\) ，我们找到它最前面的最高点 \(maxk\) ，这一定是一个 \(1\)，我们将它变成 \(0\) ，求出对应的数，就可以完成匹配。

为什么呢？考虑变化以后的图，最高点一定是 \(maxk - 1\) ，并且我们发现这个点后面的最大值原来是 \(maxk\) ，现在整体减 \(2\) 变成了 \(maxk - 2\) ，所以这个 \(maxk - 1\) 一定是最后一个 \(maxk - 1\) ，所以对于一个最高点是 \(maxk - 1\) 的数，我们将其最后一个 \(maxk - 1\) 后面的一个数变成 \(+1\)，就得到了唯一的一个有 \(k\) 个 \(1\) 的数。不用担心这个 \(maxk - 1\) 后面是否有数，顺向变化时的 \(maxk\) 下降后 \(maxk - 1\) 是它前面一个值，也就是说 \(maxk - 1\) 后面一定会有一个值，且为 \(maxk - 2\) 。

这样我们就证明了存在一部分 \(k - 1\) 个 \(1\) 的数与 \(k\) 个 \(1\) 的数的一一对应。

#include<bits/stdc++.h>
using namespace std;
const int N = 1e8 + 4e7;vector <int> p;

bitset <N> s;
int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int n,k;
	cin>>n>>k;
	int cnt = 0;
	for(int i = 1,nw = 0;i < (1 << n);++i)
	{
		if(i >= (1 << (nw + 1))) nw++;
		if(__builtin_popcount(i) == k)
		{
			++cnt;
			for(int j = nw;j >= 0;j--) 
				if((i >> j) & 1) 
					if(!s[i - (1 << j)])
					{
						s[i - (1 << j)] = 1;
						cout<<(i - (1 << j)) << '\n';
						break;
					}
		}
	}
	cerr<<1.00 * sizeof(s) / 1024 / 1024<< '\n';
	return 0;
} 

（考场上的第一种映射法。）