【数学】计算几何小结
【数学】计算几何小结
计算几何，即将几何图形在计算机中表达出来。是一门高深（毒瘤）的计算机分支。下面对近期学习的计算几何初步内容进行总结。
精度消除
精度是使无数OIer十分头疼的问题，几何平面中涉及实数，不免会使用\(double\)类型进行运算，就会产生精度问题，比如两个线段长度本来相等，但是计算中误差导致其在小数点后15位不一样，就会产生错误的判断，所以我们一般采用\(eps\)的方法，如果其绝对值小于等于\(eps\)，我们就记它为0，只要\(eps\)开得足够小，就不会出现问题。
声明：
typedef long double ld;
const ld eps = 1e-12;
判断正负（这个函数很重要！）
inline int dcmp(ld x)
{
return x < -eps ? -1 : (x > eps ? 1 : 0);
}
实数绝对值：
inline ld Fabs(ld x)
{
return x * dcmp(x);
}
向量
向量是高中数学必修一中学习的内容，这里我们用向量（一个点可以代表一个向量）进行相关运算，十分方便，而且涉及除法少，也避免了许多分讨，十分方便。
声明：
struct Point{
ld x,y;
};
#define Vector Point
向量有几个基本运算：
向量加：
Vector operator +(Vector p,Vector q)
{
return (Vector){p.x + q.x,p.y + q.y};
}
向量减：（一般用作一个点（终点）减一个点（起点）就得到两点之间的向量）
Vector operator -(Point p,Point q)
{
return (Vector){p.x - q.x,p.y - q.y};
}
数乘：（用于缩放向量）
Vector operator *(Vector p,ld q)
{
return (Vector){p.x * q,p.y * q};
}
点乘（内积）：
ld operator *(Vector p,Vector q)
{
return p.x * q.x + p.y * q.y;
}
叉乘（外积）：
ld operator ^(Vector p,Vector q)
{
return p.x * q.y - p.y * q.x;
}
模长：
inline ld Len(Vector p)
{
return sqrt(p.x * p.x + p.y * p.y);
}
点乘可以辨别一个向量与另一个向量的相对前后关系：
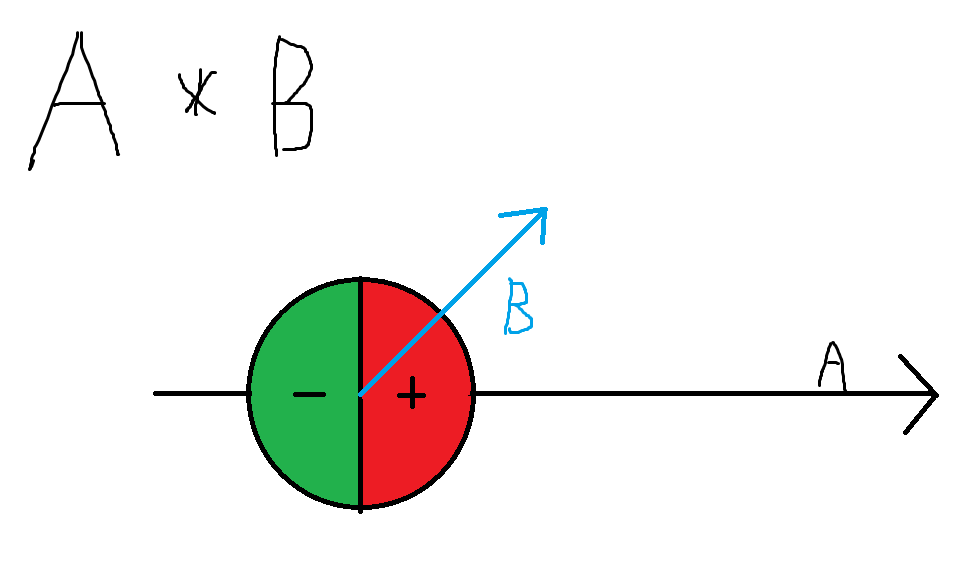
叉乘可以辨别一个向量与另一个向量的相对左右关系：
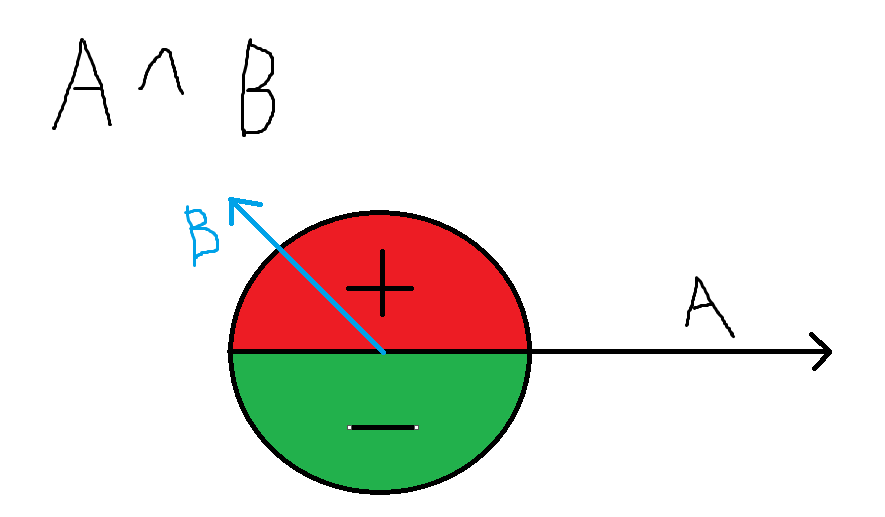
两个向量的叉积是以它们为邻边的平行四边形的有向面积：
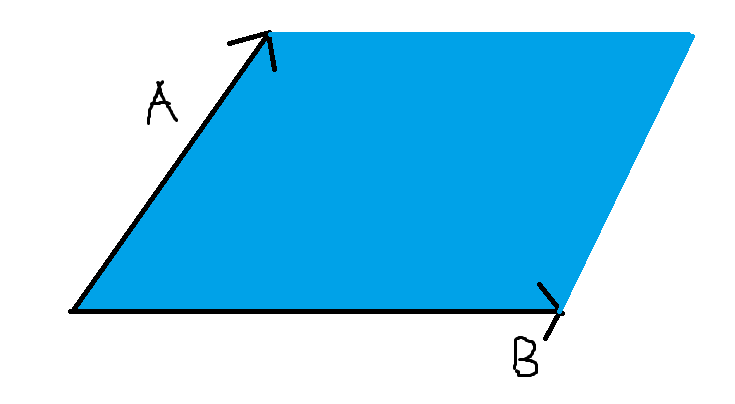
向量的极角：定义向量的极角为向量与\(x\)轴正半轴的夹角，我们一般利用c++自带的\(arctan\)函数求出夹角。
inline ld get_theta(Vector p)
{
return atan2(p.y,p.x);
}
注意是先传\(y\)再传\(x\)。
极角排序：就是将其按照极角的大小排序，但是有时我们不用求极角的办法，而是利用叉积判断两个向量之间的关系（我们简单认为一个向量极角大于一个向量当且仅当它在第二个左边）
inline bool cmp(Point p,Point q)
{
return dcmp(p ^ q) > 0 || (dcmp(p ^ q) == 0 && Len(p) < Len(q));
}
(这个是以极角为第一关键字，长度为第二关键字，从小到大排序。)
直线
一般用起点和终点来表达（有方向）：
struct Line{
Point s,t;
};
点在直线上：
直线代表向量和询问点到直线起点的向量的叉积为0，则共线。
点在线段上：
在直线上且\(x\)坐标在两点之间。
点在直线\线段左右：
叉积正\负。
线段和线段是否相交：
如果相交，那么从一个线段的端点到另一个线段的起点和终点的向量应该处于这个线段的不同侧，叉积正负值不同：
求直线交点：
采用面积法，设两个向量为\(p\)和\(q\)，所以两个向量构成的四边形的面积就是\(\frac {p_1 \times p_2}2\)（\(\times\)表示叉积）。我们记一个\(z\)，为从\(q\)的起点指向\(p\)的起点的向量，所以\(q \times z\)就是一部分的面积：
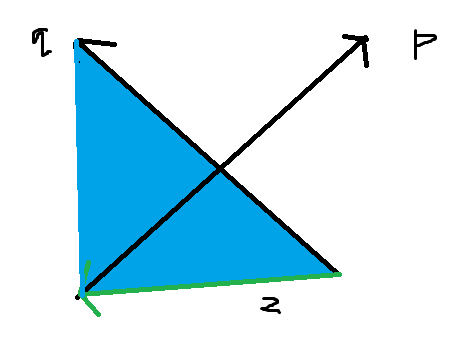
用部分面积除以总面积，就是交点到\(p\)的起点的长度与\(p\)长度的比例，将\(p\)的起点沿\(p\)方向移动那么多就可以了。
inline Point Cross(Line p,Line q)
{
Vector x = p.t - p.s,y = q.t - q.s,z = p.s - q.s;
return p.s + x * ((y ^ z) / (x ^ y));
}
注意这求的是直线的交点，就算线段不交，也会返回它们延长线的交点。
笔者对此处有一种理解：其实\(Line\)和\(Vector\)指的都是向量，但是\(Line\)是有起始位置的。
多边形
工具讲完了，终于开始讲正式的东西了。
对于多边形，存储的方式很多样，一般采用存储点集的方式。
声明：
struct Polygon{
vector <Point> pts;
};
判断是否是凸多边形：定向枚举边，看每条边拐向是否相同，即向量叉积符号是否相同。
判断点是否在多边形内部：
作一条水平射线，如果交边界次数为奇数则在多边形内（思路很妙），复杂度\(O(n)\)。
判断点是否在凸多边形内部：二分法。
以一个端点为源点，将剩下的顶点极角排序，首先二分到一个点的极角所在位置，再判断询问点与源点的连线与横穿这一区域的边是否相交。
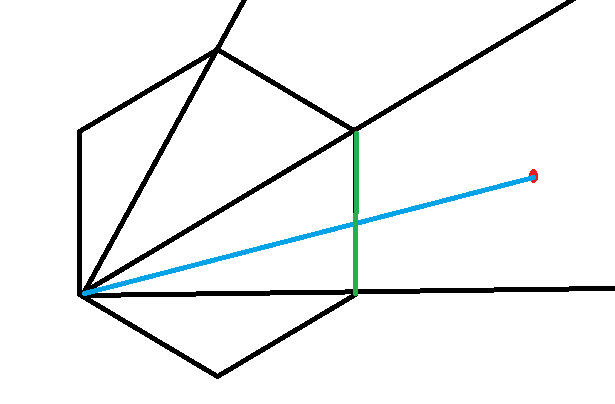
inline int sch(int l,int r,Point p,vector <Point> &c)
{
if(l == r) return l;
int mid = (l + r) >> 1;
if(((c[mid] - c[0]) ^ (p - c[0])) > 0) return sch(l,mid,p,c);
else return sch(mid + 1,r,p,c);
}
inline bool query(Point p,vector <Point> &c)
{
if((c[c.size() - 1] - c[0]) * p < 0 || p * (c[1] - c[0]) < 0) return false;
int pos = sch(0,c.size() - 1,p,c);
// cout<<c[pos].x<<" "<<c[pos].y<<" <- "<<c[pos - 1].x<<" "<<c[pos - 1].y<<endl;
return dcmp((p - c[(pos - 1 + c.size()) % c.size()]) ^ (c[pos] - c[(pos - 1 + c.size()) % c.size()])) >= 0;
}
(注意\(vector\)数组要用传址不然时空间会炸)
求多边形面积：三角剖分法，将相邻两个顶点与源点\((0,0)\)的向量叉积加起来，再除以2即可。过程详见：Computational Geometry (Polygon) - VisuAlgo（点"area"）。
凸包
凸包是指覆盖平面上 n 个点的周长最小凸多边形。
一般求凸包有两种方法：
Graham算法
先找到 y 坐标最小的点 (一定在凸包内) 加入凸包，然后对其他点极角排序后依次加入凸
包，然后不断将凸包中不符合性质的点弹出。
程序：咕
Andrew算法
先按 x 坐标排序，然后从左到右依次考虑，先找到上凸壳，然后再从右往左做一遍找到下
凸壳。
求凸壳时，凸壳必须满足斜率不断减小（不断向右拐），因此每加入一个点就和之前的进行判断，弹出不合法的即可。
inline void Andrew(vector<Point> &v)
{
int top = 0;
sort(v.begin(),v.end(),cmp);
for(int i = 0;i < v.size();i++)
{
while(top >= 2 && dcmp((v[i] - s[top]) ^ (s[top] - s[top - 1])) <= 0) --top;
s[++top] = v[i];
}
int tmp = top;
for(int i = v.size() - 2;i >= 0;i--)
{
while(top >= tmp + 1 && dcmp((v[i] - s[top]) ^ (s[top] - s[top - 1])) <= 0) --top;
s[++top] = v[i];
}
v.clear();
for(int i = 1;i <= top;i++) v.push_back(s[i]);
}
动态凸包
使用 Graham 法维护凸包，首先在凸包第一次有三个点的时候取这个三角形的重心（这个重心恒在凸包内），作为原点。
然后加入的每一个点都按照与这个原点的极角排序，存到一个 set 里面，考虑插入一个点的时候，先插进去，然后查看其前驱和后继与这个点的位置关系是否满足是沿着凸包方向折叠的。“凸包方向”有点抽象，具体的可以在纸上手模。
插入凸包的时候要判断，如果本来就在凸包里面，就不用插入了，这个可以找到前驱和后继，根据 \(pre \to suf\) 和 \(pre \to x\) 的向量外积来判断 \(x\) 究竟在里面还是外面。
细节见代码。
Point cen;
bool operator <(Point p,Point q) {return dcmp(p.theta - q.theta) ? (dcmp(p.theta - q.theta) < 0) : p.x < q.x;}
set <Point> s;
inline void init()
{
Point ori[4]; int op;
for(int i = 1;i <= 3;i++)
cin>>op>>ori[i].x>>ori[i].y; //op 没有用，是模板题 CF70D 中的操作
cen.x = (ori[1].x + ori[2].x + ori[3].x) / 3.00;
cen.y = (ori[1].y + ori[2].y + ori[3].y) / 3.00;
for(int i = 1;i <= 3;i++)
s.insert(Point{ori[i].x,ori[i].y,atan2(ori[i].y - cen.y,ori[i].x - cen.x)});
}
set <Point> :: iterator pre(set <Point> :: iterator p)
{
if(p == s.begin()) p = s.end();
p--; return p;
}
set <Point> :: iterator suf(set <Point> :: iterator p)
{
if(p == s.end()) p = s.begin();
p++;
if(p == s.end()) return s.begin();
return p;
}
inline bool inside(Point p)
{
set <Point> :: iterator it = s.lower_bound(p),id;
it = (it == s.end() ? s.begin() : it); id = pre(it);
if((((*it) - (*id)) ^ (p - (*id))) >= 0) return true;
return false;
}
inline void insert(Point p)
{
if(inside(p)) return;
s.insert(p);
set <Point> :: iterator it = pre(s.find(p)),id;
id = pre(it);
while((((*it) - (*id)) ^ (p - (*it))) <= 0) s.erase(it),it = id,id = pre(id);
it = suf(s.find(p)); id = suf(it);
while((((*it) - (*id)) ^ (p - (*it))) >= 0) s.erase(it),it = id,id = suf(id);
}
闵可夫斯基和
定义两个点集\(S_1,S_2\)的闵可夫斯基和为：
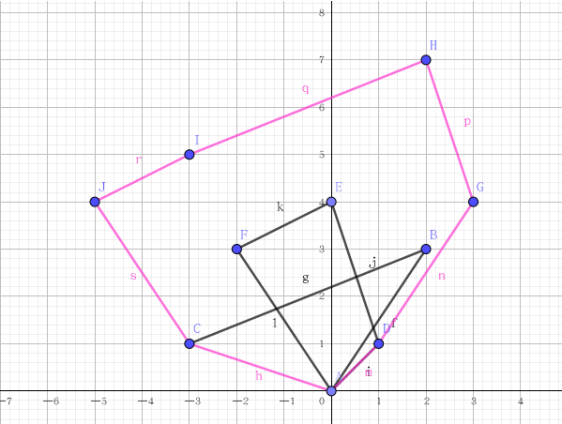
上图粉色就是四边形和三角形的闵可夫斯基和。不难发现闵和的边数等于两部分边数之和。
有以下结论：
1.两个凸包的闵可夫斯基和是一个凸包
2.任意一条A、B凸包上的边，一定是A + B的边
所以我们求出A、B的凸包，将凸包上的边极角排序，再顺次连接起来即可。
inline vector <Point> merge(vector <Point> &p,vector <Point> &q)
{
vector <Vector> vp,vq,vt;
for(int i = 1;i < p.size();i++) vp.push_back(p[i] - p[i - 1]); vp.push_back(p[1] - p[p.size() - 1]);
for(int i = 1;i < q.size();i++) vq.push_back(q[i] - q[i - 1]); vq.push_back(q[1] - q[q.size() - 1]);
int tpp = 0,tpq = 0;
Point last = p[0] + q[0]; vt.push_back(last);
while(tpp < vp.size() && tpq < vq.size())
{
if(dcmp(vp[tpp] ^ vq[tpq]) < 0) vt.push_back(last + vp[tpp++]);
else vt.push_back(last + vq[tpq++]);
last = vt[vt.size() - 1];
}
while(tpp < vp.size()) vt.push_back(last + vp[tpp++]),last = vt[vt.size() - 1];
while(tpq < vq.size()) vt.push_back(last + vq[tpq++]),last = vt[vt.size() - 1];
return vt;
}
旋转卡壳
给定平面上 n 个点，求凸包直径。
即“平面最远点对"问题。
不难发现这对点一定在凸包上，首先求出凸包，我们枚举每一条边，如果我们顺时针旋转枚举顺序，那么所对应的离这条边最远的点就一定是顺时针移动的，这个可以用双指针做到\(O(n)\)。
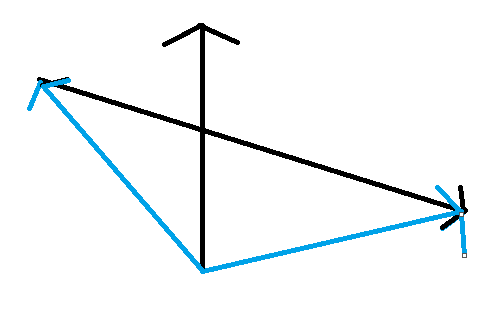
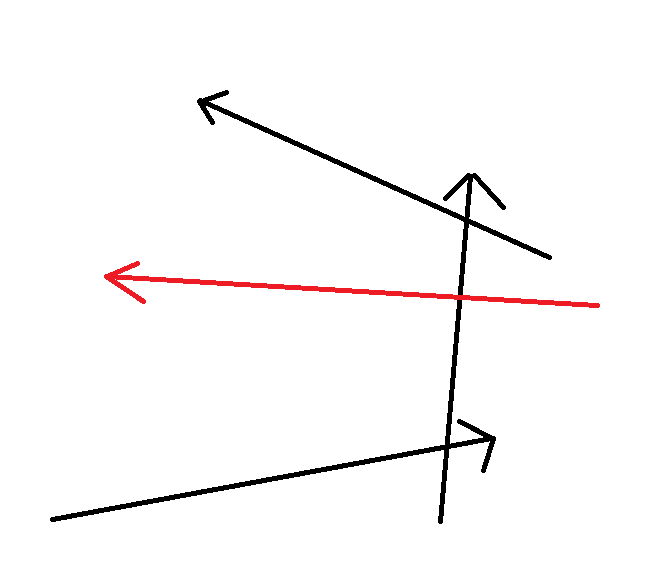
为什么和常人的直觉不一样，不能直接枚举两个点用双指针呢？因为手模可以发现，对于一个点，它和凸包上其他点的距离不是先增后降的，例如：
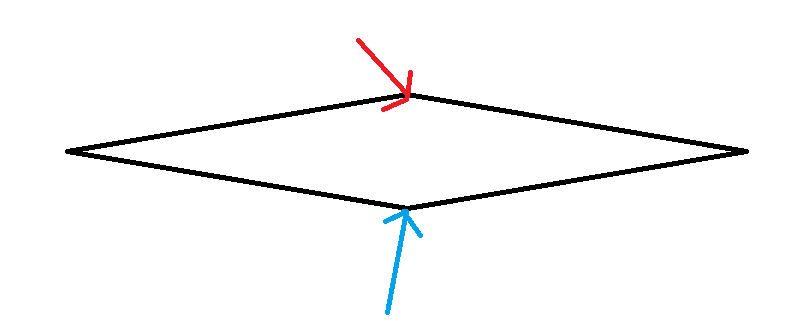
蓝色箭头到红色箭头走左半边已经先增后减了，但是走右边还会增，所以不符合单调性，但对于边，就满足这一点。
cin>>n;
for(int i = 1;i <= n;i++) cin>>a[i].x>>a[i].y;
sort(a + 1,a + n + 1,cmp);
for(int i = 1;i <= n;i++)
{
while(top >= 2 && (a[i] - s[top]) * (s[top] - s[top - 1]) <= 0) --top;
s[++top] = a[i];
}
int tmp = top;
for(int i = n - 1;i >= 1;i--)
{
while(top >= tmp + 1 && (a[i] - s[top]) * (s[top] - s[top - 1]) <= 0) --top;
s[++top] = a[i];
}
for(int i = 1;i < top;i++) b[++tail] = s[i];
for(int i = 1;i <= tail;i++) b[tail + i] = b[tail + tail + i] = b[i];
for(int i = 2;i <= tail;i++) l[i].s = b[i - 1],l[i].t = b[i];
l[1].s = b[tail];l[1].t = b[1];
ld ans = 0;
for(int i = 1,j = 2;i <= tail;i++)
{
while(Dis(b[j],l[i]) < Dis(b[j + 1],l[i])) ++j;
ans = max(ans,max(Lensq(l[i].s - b[j]),Lensq(l[i].t - b[j])));
}
cout<<(long long)ans;
半平面交
半平面交，顾名思义，就是一堆一半平面的交点。给定一些直线，其中直线的一边有效（默认是左侧），求出这些有效面的交的状态。
对于半平面交问题，我们采用\(S \& I\)算法。首先对这些直线进行极角排序，然后去除斜率相同的直线，由于取左半边，我们就保留最左的一条。将这些直线顺次加入一个队列，每次用新加入的元素更新，对于一个新加入的直线，如果原来两直线的交点在其右边，这个交点就作废，发现一个事实，就是这两直线只可能是队首和队尾（凸包两端）的直线（就算中间的直线交点也在右边，某一端的交点也会靠的更右），所以每次先更新队尾，再更新队首。
其实还不止如此，半平面交可能成为一个闭合凸包，所以队尾元素需要满足队头的约束，我们可以看成要将队头元素插入，用同样的方式更新队尾即可。
如果最后删得只剩一条边，那么有两种情况：1.没有交 2.最后一条边是最高的。
inline Polygon inter()
{
Polygon ret;
int head = 1,tail = 0;
Line q[1005];
q[++tail] = l[1];
q[++tail] = l[2];
for(int i = 3;i <= cnt;i++)
{
while(head < tail && dcmp(Cross((cross(q[tail - 1],q[tail]) - l[i].s) , (l[i].t - l[i].s))) >= 0) --tail;
while(head < tail && dcmp(Cross((cross(q[head],q[head + 1]) - l[i].s) , (l[i].t - l[i].s))) >= 0) ++head;
q[++tail] = l[i];
}
while(head < tail && dcmp(Cross((cross(q[tail - 1],q[tail]) - q[head].s) , (q[head].t - q[head].s))) >= 0) --tail;
if(head == tail) return ret;
q[++tail] = q[head];
for(int i = head + 1;i <= tail;i++)
ret.pts.push_back(cross(q[i],q[i - 1]));
return ret;
}
初步的计算几何就讲到这里，主要是如何将这些技巧掌握熟练和应用上面。
完结撒花。
