2023.3.24 【字符串】KMP 算法

题目描述

有这样一个问题：

给定 $n$ 个模式串 $s_i$ 和一个文本串 $t$，求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。

题面多简单qwq

如果我们简化一下这个问题，模式串和文本串都只有一个，那么我们就可以用一个10行就能写完的算法——KMP字符串匹配来解决问题。

我们在匹配之前，先将这个模式串“自匹配”，设数组$next[i]$表示模式串前$i$个字符能进行自匹配的最大长度，这里我们定义“自匹配”：

如果字符串s的前k个字符等于后k个字符，且k是满足条件的最大值，那么我们就说k是s自匹配的最大长度。

从1到n(长度)循环，如果$s[next[i-1]+1]==s[i]$，那么$next[i]$就可以由$next[i-1]$延续而来，由于$next[i-1]$是最大值，$next[i]$一定是最大值(匹配长度最多增加一位)

如果不等于，说明当前匹配长度$next[i-1]$无法延伸到$next[i]$，我们称这种情况叫做失配，失配后我们需要找到备选答案，即满足对于前$i-1$个字符（第i个尚未匹配），有前k个字符等于后k个字符，但是k是小于$next[i-1]$的（因为$next[i-1]$不可取），然后再检验$s[k+1]$是否等于$s[i]$。我们要想办法不重不漏、从大到小地选择这样的k值。

我们观察到一个性质，由于前i - 1个字符中，$next[i-1]$已经是前后匹配的最大值，所以对于$k<next[i-1]$，前$next[i-1]$这一段的后k个字符一定等于前$i-1$个的后k个字符，也就是说，$s[next[i-1]-k+1]\to s[next[i-1]]==s[i-k]\to s[i-1]$

然而我们又要$s[1]\to s[k]==s[i-k]\to s[i-1]$

所以$s[1]\to s[k]==s[next[i-1]-k+1]\to s[next[i-1]]$

注意到，前$next[i-1]$个字符中，前k个等于后k个，又因为我们要k除$next[i-1]$外的最大值，所以根据定义 ，我们要的k就是$next[next[i-1]]$

如图：

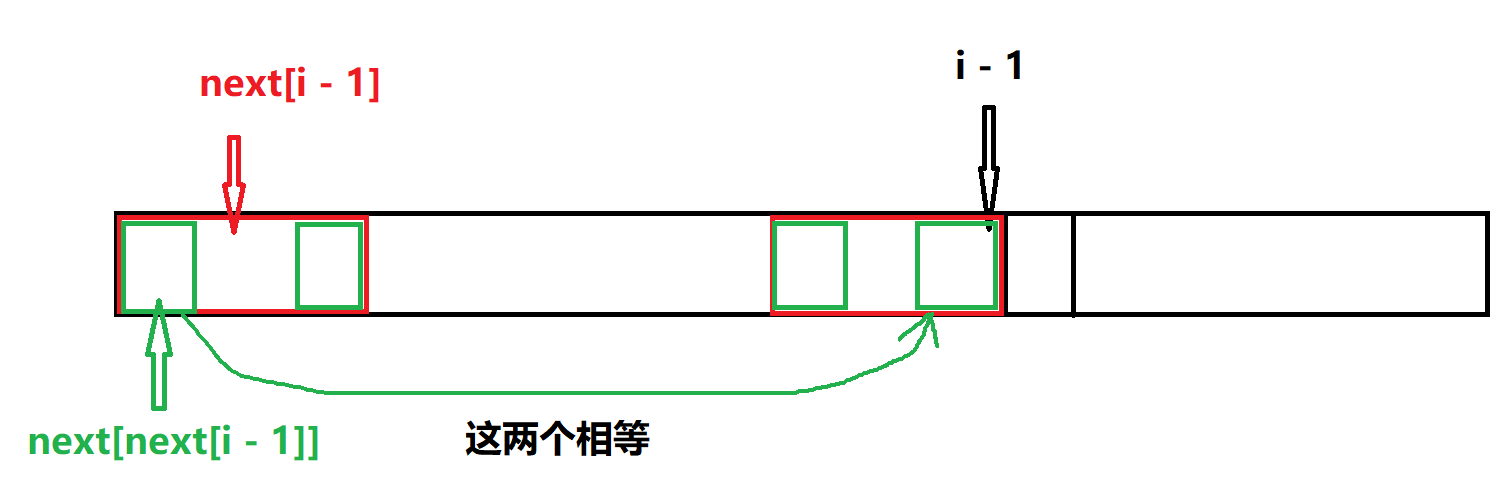
完成自匹配后，其实文本串和模式串匹配是一样的，记录当前$t[i-1]$的最大匹配长度k，i每次增加是检验$t[i]$与$s[k+1]$是否相等，如果不相等，就将$k=next[k]$再匹配即可，当$k==s.length$时，就是s在t中的一次出现。

Code

for(int i = 2,j = 0;i <= n;i++)
{
	while(j > 0 && s[i] != s[j + 1]) j = next[j];
	if(s[i] == s[j + 1]) j++;
	next[i] = j;
}
for(int i = 1,j = 0;i <= m;i++)
{
	while(j > 0 && (t[i] != s[j + 1] || j == n)) j = next[j];
	if(t[i] == s[j + 1]) j++;
	f[i] = j;
	if(j == n)
		otp.push(i - j + 1);
}

（此处s和t都从1开始）

这时向前看，我们就会发现$next$数组多了一种意义：当前模式串的前i个匹配后，如果失配了，接下来应该匹配模式串的前几个。相当于为我们指明了当前状态失配后应该转移到哪里去。这个在后来的AC自动机，PAM和SAM中都是十分普遍的概念。我们后来叫它fail数组，即“失配数组”。

KMP算法的复杂度是O(n + m)的，因为它的两个循环分别次数为n 和 m ，对于当前记录的长度k（即程序里的j），每次只会向后+1,而减少的量不会多于增加的量，所以最多移动2n个单位，复杂度也是$O(n)$的。