随机算法
算法导论
这个文档是学习“算法设计与分析”课程时做的笔记,文档中包含的内容包括课堂上的一些比较重要的知识、例题以及课后作业的题解。主要的参考资料是 Introduction to algorithms-3rd(Thomas H.)(对应的中文版《算法导论第三版》),除了这本书,还有的参考资料就是 Algorithms design techniques and analysis (M.H. Alsuwaiyel)。
随机算法
这里将会讨论另一种形式的算法,放宽算法对所有可能的输入都必须得到正确解的要求,允许其可能会得到不正确的结果,这个可能的不正确性能够因为其出现的概率极低而被安全忽略。并且也不再要求算法每次运行某个特定的输入都必须得到相同的结果,而是希望算法在执行过程中能够掷硬币,产生真正随机的结果。
引入随机性并不会产生不可预测的结果,而是非常有用,并且能够为非常低效的确定性算法提供快速解决的方案。
在构建算法的过程中,随机化是一个非常重要的工具,因为随机化的算法能够比确定性的算法使用更少的时间和空间成本,并且随机化的算法通常也更加容易理解和实现。
随机算法可以被定义为除了输入之外还接收随即比特流的算法,算法可以在其操作过程中使用这个比特流来进行随机选择。
下面看一个例子,比如现在有一个 n 元多项式 \(f(x_1,x_2,...,x_n)\) ,并且希望确定这个多项式是否是恒等于0的。
如果要使用对 n 个变量逐个验证的方法,那么工作量将会是非常恐怖的。然而,如果使用随机化的方法,随机生成一个 n 维向量 \((v_1, v_2,...,v_n)\) 并带入这个多项式,如果 \(f(v_1,...,v_n)\ne 0\),那么这个多项式就不为0;否则,如果 \(f(v_1,...,v_n) = 0\) 那么重复上面的步骤进行验证,如果几次验证的结果都为0,那么 f 大概率是恒等于 0 的多项式,也就是说这种情况下 f 不等于 0 的概率是可忽略的。
在一些确定算法中,尤其是那些表现出良好的平均运行时间的算法,只需要引入随机化就能够避免其糟糕的最坏情况,并使得该算法能够在每种可能的结果以高概率良好执行。
随机算法可以分为两类:Las Vegas算法和Monte Carlo算法,下面将会分别讨论这两种算法。
不过在正式开始之前有必要介绍衡量随机算法性能的标准。
对于一个确定的算法 A ,衡量其性能的时间复杂度是指该算法的平均运行时间,也就是对所有可能的输入大小 n 的平均运行时间。这里假设所有可能的输入都是均匀分布的,不过实际情况也有可能不是均匀分布的。
对于一个随机的算法 A ,那么对于一个大小为 n 的固定实例 I ,该算法所使用的时间可能会发生变化。因此对于随机算法的性能评估标准是算法 A 运行在固定实例 I 的运行时间的期望。也就是使用算法 A 一次又一次的在实例 I 上运行的平均运行时间。
Las Vegas algorithm
Las Vegas算法是指总是给出正确答案或者不给出答案的随机算法。
比如现在有一个数组 A[1...n],其中 n 是偶数,这个数组中有 (n/2) + 1 个元素取值都为 x ,而剩下的 (n/2) - 1 个元素的取值都与 x 不同,现在希望找到这个重复的元素 x,使用Las Vegas算法的伪代码如下:

代码中的 "sample" 是指以均匀的概率随机采样,后面出现这个词也是一样的意思。
令 \(\Pr[success]\) 表示一次迭代中 \(i\ne j A[i] = A[j]\) 的概率,则:
\(\Pr[success] = \frac{n/2 + 1}{n}\times \frac{n/2}{n} \gt \frac{n/2}{n} \times \frac{n/2}{n} = \frac{1}{4}\)
因为第一次选择重复的元素有 n/2 + 1 中可能,第二次选择有 n/2 中可能。
那么一次迭代中失败的可能性就为 \(\Pr[failure] \le 3/4\)。那么 k 次迭代都失败的可能性为小于或者等于 \((3/4)^k\) 。因此,在 k 次迭代内成功的概率为\(1-(3/4)^k\)。
为了将这个概率写成 \(1-(1/n)^c\) 的形式,令 \((3/4)^k = (1/n)^c\),则 \(k=c\log_{4/3}n\)。也就是说比如令c = 4,则该算法能够以 \(1-1/n^4\) 概率在 \(O(\log_{4/3} n)\) 的时间复杂度内得到正确的答案。
需要注意的是,在Las Vegas算法中,概率与其运行时间相关,而结果总是正确的。
Monte Carlo algorithm
Monte Carlo算法是指总是给出答案,但是有时会给出错误答案的算法,但是给出错误答案的概率很低,可以忽略。
比如现在有一个数组 A[1...n],其中 n 是偶数,现在希望能够从该数组中找到一个大于中位数的数,使用Monte Carlo算法的伪代码如下:
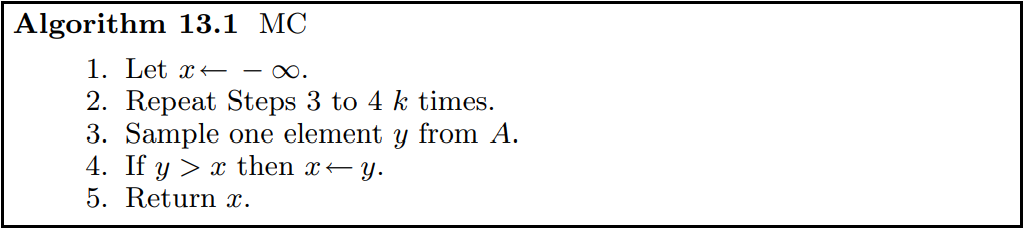
显然,上述算法迭代一次失败的概率,即采样的元素大于中位数的概率为 1/2,那么 k 次迭代失败的概率为 \(1/2^k\),所以 k 次迭代后采样到一个大于中位数的概率为 \(1-1/2^k\)。
同样,为了将这个概率写成 \(1-1/n^c\) 的形式,令 \(1-1/2^k = 1-1/n^c\),则 \(k=c\log n\),也就是说比如令,c=4,则该算法能够在 \(O(\log n)\) 的时间复杂度内以 \(1-1/n^4\) 的概率得到正确解。
需要注意的是,在Monte Carlo算法中,概率与正确性相关,而运行时间是固定的。
在另一个文件中的算法笔记中,介绍了随机算法在快速排序和选择问题中的应用。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号