回溯法
算法导论
这个文档是学习“算法设计与分析”课程时做的笔记,文档中包含的内容包括课堂上的一些比较重要的知识、例题以及课后作业的题解。主要的参考资料是 Introduction to algorithms-3rd(Thomas H.)(对应的中文版《算法导论第三版》),除了这本书,还有的参考资料就是 Algorithms design techniques and analysis (M.H. Alsuwaiyel)。
回溯法
在现实世界中,大多数问题都可以通过搜索大量但是有限的可能性来找到解决方案。
此外,对于几乎所有这些问题,不存在使用穷举搜索以外的方法来得到解决方案。因此,希望能够有一种更加系统的搜索方法,将搜索空间尽可能地缩小,从而提高效率。
这种用于系统搜索的通用技术被称为回溯法(backtracking),而回溯法可以理解为一种能够避免搜索所有可能的结果的组织性穷举搜索(organized exhaustive search)。
在回溯法中,问题的解空间可以被组织成一个解空间树或者搜索树(search tree),并且使用深度优先的方法进行搜索,算法搜索至解空间树的任意节点时,先判断该节点是否能够达到正确的解,如果肯定不能到达正确的解,则跳过以该节点为根节点的子树的搜索,逐层向其祖先节点回溯;否则,进入该子树,继续按深度优先的方法搜索。
下面回顾一个之前在介绍贪心法时介绍过的问题————背包问题。现在将会演示如何使用回溯法解决背包问题。
假设现在有三个物品,每个物品的重量分别为(20, 15, 10),每个物品的价值分别为(20, 30, 25),背包的容量为25。
下图为使用回溯法搜索解空间树的过程:
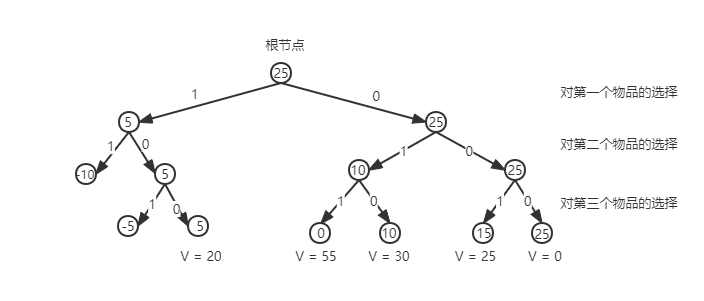
路径上的1,0分别表示选择该物品或者丢弃该物品,节点中的数值表示当前背包的容量,可以看到当背包的物品的容量为负数时必然不可能得到正确的解决方案,那么就向父节点回溯,寻找其他解决方案。使用回溯法可以找出所有可能的方案,并且可以避免搜索所有可能的结果。
3-着色问题
3着色问题(3-coloring problem),给定一个无向图 G = (V, E),要求为图中每个节点涂上三种颜色(denoted as 1, 2, 3)中的一种,并且任意两个相邻的节点不能使用相同的颜色。
可以将每个节点的着色方案表示为一个n元组 \((c_1, c_2,...,c_n),c_i\in \lbrace 1, 2, 3 \rbrace\) ,比如 (1, 2, 2, 3, 1)表示图中 5 个节点的着色方案。那么这个问题的解空间中包含 \(3^n\) 种可能。
比如下面的例子,要给一个包含5个节点的无向图着色:
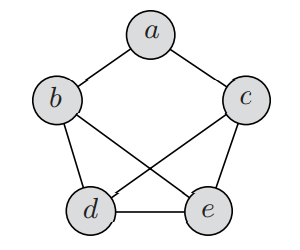
下图是使用回溯法找到一种有效解决方法的过程:
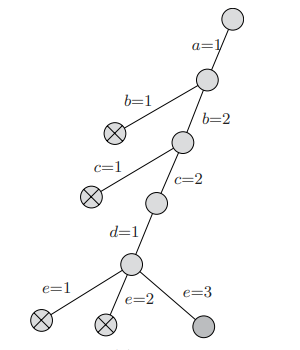
上图对应的着色方案是 (1, 2, 2, 1, 3)。注意,上图只是找到一种的解决方法,而没有完整地搜索整个解空间树并找到所有有效的解决方法。
在上面的例子中需要注意的是,首先,节点是按照深度优先的顺序生成的;其次,没有必要保存整个解空间树,而只需要保存从根节点到当前节点的路径即可。事实上,并没有真正生成节点,而解空间树存在于概念上,并不是实际存在的,只需要追踪着色分配即可。
3-着色问题的回溯算法的伪代码如下:

这里给出的算法是使用嵌套循环实现的,实际上这个算法也可以使用递归的方式实现。在这个伪代码中,内层的循环用于生成新的节点,即对每个节点依次遍历3中可能的颜色,然后查看当前的着色方案是否是能够得到正确方案的(partial)或者是合法的解决方案(legal coloring);外层的循环用于回溯,如果发现当前的着色方案不可行,那么就回到上一个节点。
通用的回溯方法
回溯法通常作为一种系统搜索的方法,用于解决的搜索问题的解决方案通常由满足预定义的限制条件的向量 \((x_1, ..., x_i)\) 组成,其中 i 可以是 0 到 n 的任意整数,n 是问题的规模。
在前面介绍的3-着色问题或者另一个比较经典的8-皇后问题中,i 都是固定为 n 的,然而 i 其实是可变的,也就是说同一个问题的不同解向量(solution vector)的长度可能是不一样的。
比如下面的这个例子,给定一个包含 n 个整数的集合 \(X=\lbrace x_1, x_2, ..., x_n \rbrace\) 以及一个整数 y ,找到 X 一个子集,使其中元素的和恰好等于 y,比如下面这样:
X = {10, 20, 30, 40, 50, 60} , y = 60,那么就有下面不同的解决方案:{10, 20, 30}, {20, 40}, {60}。
很容易通过回溯的方法找到这个问题的解,思路和前面提到背包问题类似,这些解的长度都是不固定的。
当然也可以使用n维的布尔元组来表示上面这个问题的解,比如上面的解也可以表示为 {1, 1, 1, 0, 0, 0}, {0, 1, 0, 1, 0, 0}, {0, 0, 0, 0, 0, 1}。
在回溯法中,解向量的每一个分量 \(x_i\) 都属于一个有限的集合 \(X_i\),因此,回溯法相当于是按照字典顺序考虑笛卡尔积 \(X_1\times X_2\times \cdots X_n\) 中的元素。
最初,算法从一个空向量(empty vector)开始,随后选择集合 \(X_1\) 中最小的(least)一个元素作为解向量的第一个分量 \(x_1\)。如果 \((x_1)\) 是部分解(即能够得到正确解的),那么算法将会继续选择第二个集合 \(X_2\) 中最小的元素最为解向量的第二个分量 \(x_2\)。如果 \((x_1, x_2)\) 是部分解,那么将会选择第三个集合 \(X_3\) 中的最小元素作为解向量的第三个分量;否则,将会选择 \(X_2\) 中的另一个元素作为解向量的第二个分量。
更一般地讲,如果算法已经得到了一个能够得到正确解的(partial)解向量 \((x_1, x_2, ..., x_j)\),那么考虑向量 \(v = (x_1,x_2,...,x_j,x_{j+1})\) 将会有下面几种情况:
- 如果 v 表示一个最终的解,那么就将其记录为该问题的一个解。算法要么终止要么继续,取决于是否要找到多个解;
- (The advance step): 如果 v 表示一个部分解,那么就算法将会进而选择 \(X_{j+2}\) 中最小的元素;
- 如果 v 既不是最终解也不是部分解,那么将会有两种情况考虑:
- 如果在集合 \(X_{j+1}\) 中还有别的可选元素,那么解向量的 \(x_{j+1}\) 将会选择该集合的下一个元素
- (The backtrack step) 如果集合 \(X_{j+1}\) 中没有别的可选元素,那么算法将会选择 \(X_j\) 集合中的下一个元素;如果 \(X_j\) 中也没有别的可选元素,那么将会回溯到 \(X_{j-1}\) 集合。并按此规律回溯。
下面给出通用回溯法的伪代码:

上面的伪代码是使用迭代实现的,当然也可以使用递归的方式实现。和前面介绍的例子一样,内层的循环用于向前组织解向量(the advance step),外层的循环用于回溯(the backtrack step)。
通常,为了使用回溯得到搜索问题的解,可以使用上述的算法作为框架,围绕该框架可以设计专门针对手头问题定制的算法。
分支限界
分支限界与回溯法十分类似,也是生成解空间树来寻找一个或多个解。然而回溯法用于搜索满足某一属性的解,而分支限界通常只关心某个给定函数的最值。
此外,在分支限界算法会在每个节点 x 处计算一个界限,即以该节点 x 为根节点的子树所给出的所有可能解的取值界限。如果这个界限比之前计算出的界限更加糟糕,那么就丢弃以 x 为根节点的子树,即不会再以该节点生成子节点。也就是对于任何一个部分解 \((x_1,x_2,...,x_{k-1})\) 以及它的扩展 \((x_1,x_2,...,x_k)\) 必须满足下面的关系:
\(cost(x_1,x_2,...,x_{k-1}) \le cost(x_1,x_2,...,x_k)\)
由于这样的关系,如果想要找到一个代价为 c 的解,并且有一个部分解的代价至少是 c ,那么就不会再继续扩展这个部分解。
分支限界中的一个经典问题是旅行售货员问题(Traveling Salesman Problem, TSP)。
给定一个有向图,图中每个节点代表一个城市,城市间的路径就是图中的边,路径的长度通过邻接矩阵给出。旅行售货员会以封闭的路径访问这些城市,也就是访问每个城市并回到起点,且每个城市只去一次,求满足要求的最短路径。下图就是一个代表路径长度的邻接矩阵:
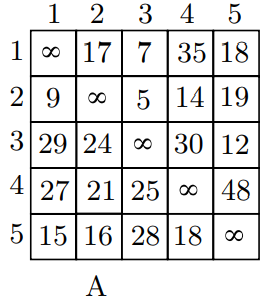
对于给定部分解 \((x_1,x_2,...,x_k)\) ,定义这个解的成本下限为按照 \(x_1,x_2,...,x_k\) 的顺序旅行过这些城市的最低成本。
对TSP问题,可以观察到的是,那么为了对每个城市都访问仅一次并且回到起点,假设有 n 个节点,那么就需要 n 条边,并且这 n 条边是分别落在不同行不同列的。为了定义成本下限,可以从成本矩阵(cost matrix)中的每一行和每一列都选择一条边,然后对该行或者该列减去一个数值使得选中的边变为0,这样,矩阵的每一行和每一列都会包含一个0。如下图所示:
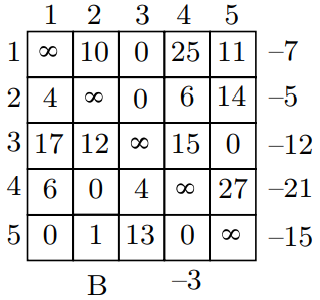
由矩阵 A 得到上面这个矩阵 B 的方法很简单,每行先减去该行最小的值,减完后发现第 4 列还没有包含 0 的值,于是对第 4 列减去该列最小的值,得到该矩阵。
将每行和每列减去的数值加起来,就是当前的成本下限。比如上图中的成本下限就是 63。
下图是使用分支限界的方法寻找最优解的搜索树,从(3,5)边开始,后面会解释为什么从这条边开始。从该节点开始,生成两个子节点,右边的子节点不包含(3,5)边,即以该节点为根节点的子树中解中不会包含(3,5)边,将 (3,5) 置为无穷大后的计算矩阵 D 的成本下限:
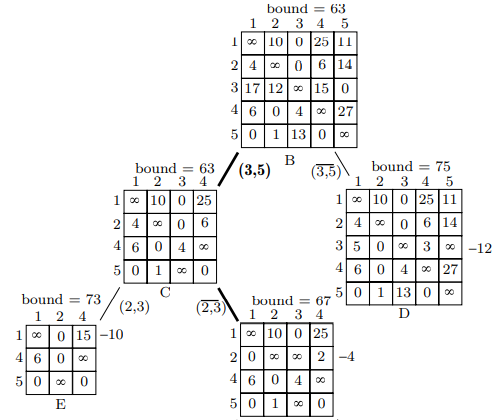
在矩阵 D 中,由于第三行不包含 0,所以需要在第三行将去12,那么成本下限就变成了75。
左边的子节点包含(3,5)边,如果选择了这条边,那么将无法从节点3到达除节点5以外的任何节点,也无法从除节点3以外的任何节点到达节点5,所以除去矩阵 B 第 3 行第 5 列得到矩阵 C 并计算成本下限,并且将第 5 行第 3 列置为无穷大,然后计算矩阵 C 的成本下限,因为每行每列都包含0,因此矩阵 C 的成本下限不变,和父节点一样是 63,比矩阵 D 的成本下限低,因此接下来考虑矩阵 C 的(2,3)边生成子节点。
分支限界与回溯的另一个区别在于,回溯总是深度优先的搜索,而分支限界则是将节点放入一个优先级队列,按照优先级队列的顺序进行搜索。
按照上面的规律可以得到完整的搜索树如下:
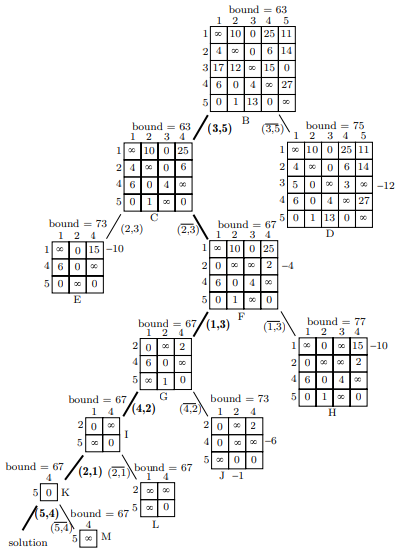
所以得到的最优解为:\(1\to 3\to 5\to 4\to 1\to 2,\to 1\),该路径总成本为 7 + 12 + 18 + 21 + 9 = 67。
在上面生成搜索树的过程中生成子节点所选择的边主要是考虑尽可能生成比较少的节点而得到最优解。所以一开始选择(3,5)边是为了让右边子节点的成本下限得到最大的增加,这样以右边子节点为根节点的子树的优先级就会降低很多。
尽管分支限界算法通常都是复杂且难以编程的,但在实际应用中确实是高效的。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号