贪心法
算法导论
这个文档是学习“算法设计与分析”课程时做的笔记,文档中包含的内容包括课堂上的一些比较重要的知识、例题以及课后作业的题解。主要的参考资料是 Introduction to algorithms-3rd(Thomas H.)(对应的中文版《算法导论第三版》),除了这本书,还有的参考资料就是 Algorithms design techniques and analysis (M.H. Alsuwaiyel)。
贪心法
与动态规划一样,贪心法通常用于解决最优解的问题。但是与动态规划不同的是,贪心法通常由试图找到局部最优解的迭代过程组成。
贪心法与动态规划的另一个区别在于,贪心法是迭代的,而动态规划是递归的。
贪心法得到的解并不总是全局的最优解。
贪心法得到的解决方案通常是一步一步的(step by step),每一步都是在局部范围内在很少计算的基础上作出正确的猜测,而不用担心未来。
能够使用贪心法解决的问题通常具备两种性质:
- 最优子结构
- 贪心选择性
其中最优子结构性质和动态规划问题中的最优子结构性质是一样的。
而贪心选择性则是指一个问题的全局最优解可以通过局部最优解得到,或者说通过贪心法得到的解决方案是正确的,而这部分的证明通常是设计贪心算法最难的部分。
下面介绍一个简单的例子,背包问题。
假设现在有 n 件物品,每件物品的大小为 \(s_1,...,s_n\) 每个物品的价值为 \(v_1, ..., v_n\),现在有一个容量为 C 的背包来装这些物品,如何选择使得在背包容量的限制下装取的物品的价值总和最大?
这个问题使用贪心法就很好解决,先计算物品的性价比,\(r_i = v_i / s_i\),然后将所有物品按照性价比由高到低排序,然后按照这个排序进行选择,直到背包容量已满。
上面的这个方法就体现了贪心算法的局部最优性,迭代进行,每次都选择当前剩余物品中性价比最高的物品。
Minimum Cost Spanning Trees(Kruskal)
贪心法一个比较经典的使用场景是最小生成树。
最小生成树的定义:设 G = (V, E) 是一个无向连通图(connected undirected graph),并且每条边都有其权重。G 的一个生成树 (V, T) 是 G 的一个子图,并且是一个树,也就是说没有回路。如果 T 中每条边的权重之和是最小的,那么就称 (V, T) 是最小代价生成树(Minimum Cost Spanning Trees),或者最小生成树(Minimum Spanning Trees)。
Kruskal 的方法原理是,维护一个由几个生成树组成的森林,然后将森林中的生成树逐渐合并,直到将所有生成树合并成一个树,这个树就是最小生成树。
算法的具体步骤分为两步:
- 将 G 中所有的边按递增的顺序排序;
- 迭代选择图中的边,每次都选择最短的一条边:对于有序列表中的每一条边,如果这条边没有与 T 中的边构成回路,就将其放入 T 中;否则就丢弃这条边。
下面给出一个列子:
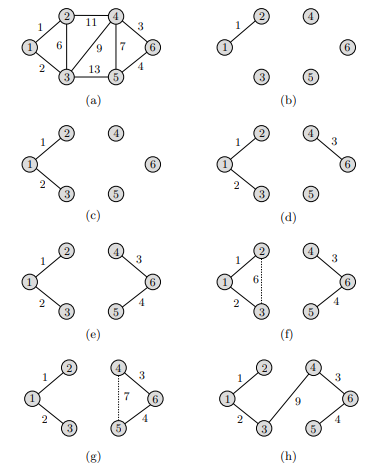
实现
Kruskal 的最小生成树算法的实现需要使用并查集(Disjoint Set) 来判断当前的树中是否包含回路。
并查集相当于是一个森林,通常由数组实现,disjoint_set[i] 表示元素 i 的父节点,如果父节点是其本身,那么就意味着这个节点是其所在的树的根节点。初始阶段,每个节点的父节点都是其本身,然后通过合并而形成一个树。
并查集常用的有两种操作:查,找到目标元素所在的树的根节点;并,将两个两个不同的树合并成一个树。
Kruskal's algorithm:

上图给出了该算法实现的伪代码,其中的 MAKESET() 是指初始化一个并查集。
正确性
下面证明 Kruskal 算法的正确性。
需要使用到的定理:
If T is a tree with n vertices, then
(a) Any two vertices of T are connected by a unique path.
(b) T has exactly n − 1 edges.
(c) The addition of one more edge to T creates a cycle.
使用数学归纳法求证,对最小生成树所包含的边的集合 T 的大小进行归纳:
贪心问题的贪心选择性的证明常用数学归纳法求证。
最初,T = { } ,那么 T 显然是 T* 的一个子集。其中 T* 是最小生成树 G* = (V, T*) 中的边的集合。
假设 \(T\subset T^*\)。随后,在使用Kruskal算法添加一条边 e = (x, y) 到 T 中之前,令 X 为包含节点 x 的子树节点的集合。
令 \(T' = T\cup \{e\}\),可以证明 T' 依然是 T* 的一个子集:
i. 如果 \(e\in T^*\),那么 \(T'\subset T^*\) 显然成立。
ii. 如果 \(e\notin T^*\),则:
根据上面的定理,\(T^* \cup \{ e\}\) 中会包含一个回路,而 e 正是这个回路中的一条边。而 e = (x, y) 连接了 X 中的一个节点和 V-X 中的一个节点。那么 T* 中也必然存在一条边 e' = (w, z) ,其中 \(w\in X, z \in V-X\),才能在 T* 中形成回路。
那么有 \(cost(e') \ge cost(e)\),否则根据Kruskal算法 e' 会先于 e 加入 T。现在构造 \(T^{**} = (T^* - \{e'\}) \cup \{e\}\),那么 \(T'\subset T^{**}\)。
此外,\(T^{**}\) 也是包含最小生成树中所有边的集合,因为 e 是连接 X 中的节点与连接 V - X 中的节点的最短路径。
即 \(T\cup \{e\}\) 依然是最小生成树中所有边的集合的子集。
那么根据归纳法,通过Kruskal算法添加边得到的集合一定都是最小生成树所有边的集合的子集,直到这个集合的边能够连通 V 中的所有节点,得到最小生成树。
Minimum Cost Spanning Trees(Prim)
解决最小生成树问题还有另一个算法——Prim's algorithm。这个算法与Kruskal的算法完全不同,但同样也是使用贪心的策略进行决策。
Prim的算法以图中的任意一点为起点来生成最小生成树。令 G=(V, E) 为一个连通无向图,将 V 中节点编号为 {1, ..., n},初始时,令 X = {1}, Y = {2, ..., n},算法依然是迭代进行,每次迭代添加一条边,而这条边是节点 \(x\in X, y\in Y\) 的最短路径 (x, y)。添加这条边到最小生成树中所有边的集合 T 中,并且将节点 y 从集合 Y 中移除并加入到集合 X。不断迭代,直到集合 Y 为空集,得到最小生成树。
步骤如下:
- \(T\gets \{\}, X\gets \{1\}, Y\gets V - \{1\}\)
- 令 (x,y) 为集合 X 到集合 Y 中节点的最短路径,则 \(X\gets X\cup \{y\}, Y\gets Y-\{y\}, T\gets T\cup \{(x,t)\}\)
- 重复步骤2,直到 \(Y=\{\}\)
下面给出一个例子:
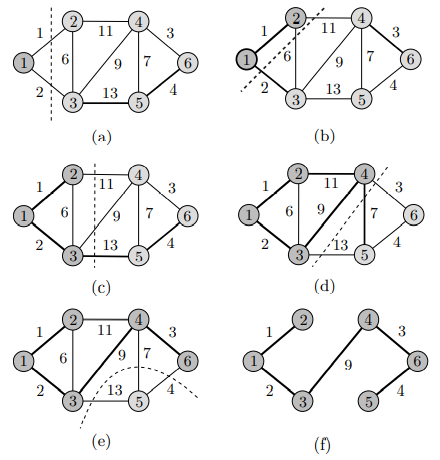
实现
Prim的算法使用邻接矩阵来实现,即矩阵 c[i,j] 表示边 (i, j) 的长度。然后使用 boolean 类型的一维数组 X[n], Y[n] 来表示集合 X, Y:

上图为Prim算法的伪代码。
正确性
下面证明Prim算法的正确性。
同样的,使用归纳法进行证明。对集合 T 的大小进行归纳,可以证明 (X, Y) 是图 G 最小生成树的一个子树。
起初,T = { },上面的结论显然成立。
假设上面的结论在添加一条边 e = (x, y) 到集合 T 之前都是成立的,即 (X, T) 是最小生成树的一个子树,其中 \(x\in X, y\in Y\)。令 \(X' = X\cup \{y\}, T' = T\cup \{e\}\),那么可以证明,{X', T'} 依然是图 G 最小生成树的一个子树。
首先证明 (X', T') 是一个树。因为 \(y\notin X\),并且 (X, T) 本身是一个树,所以边 e = (x, y) 不会在 T' 中构成回路,即 (X', T') 是一个树。
现在证明 \(T' = T\cup \{e\}\) 是 G 的最小生成树的一个子树。设图 G 的最小生成树为 G* = (V, T*)。
i. 若 \(e\in T^*\) ,那么结论显然成立。
ii. 若 \(e\notin T^*\),那么根据前面的定理,\(T^*\cup \{e\}\) 必然包含一个回路。
这也就意味着 T* 中包含一条边 \(e' = (w, z), w\in X, z\in Y\)。
那么根据 Prim 算法,只有\(cost(e') \le cost(e)\) 才能够使 \(e'\in T^*\),而这与 e 是集合 X 与集合 Y 节点间最短路径的前提矛盾。所以必然有 \(e\in T^*\)。
因此 \(T' = T\cup \{e\} \subset T^*\)
综上,使用Prim算法得到的集合 (X, T) 是图 G 最小生成树的一个子树,直到 Y = {} 时,得到最小生成树。
Huffman编码
贪心法的另一个比较经典的使用案例是用于文件压缩的Huffman编码。
假设现在有一个文件,由字符串组成。现在希望尽可能多地压缩这个文件,并且能够轻易还原。假设文件中的字符集合为 \(C = \{c_1, ..., c_n\}\),令 \(f(c_i)\) 为字符 \(c_i\) 在文件中出现的频率,也就是出现的次数。
以固定长度的比特串来表示每个字符,也就是字符编码,那么文件的大小就取决于文件包含的字符总数。
然而,为了减小文件的大小,因为文件中某些字符出现的频率会远高于其他字符,所以可以考虑使用变长(variable-length)的编码方式,并且为出现次数比较高的字符分配更短的比特进行编码。
在变长编码中,需要注意某个字符的编码一定不能是另一个字符编码的前缀,这样的编码方式称为前缀编码(prefix codes)。比如,如果对字符 'a' 的编码为 "10", 对字符 'b' 的编码为 "101" 那么在扫描文件的时候就会出现二义性,也就是说 "10" 应该解释为字符 'a' 还是字符 'b' 的前缀呢?
如果编码方式满足了这样的限制,那么扫描文件时可以用下面的方式进行正确解码。使用一个完全二叉树,每个节点连接子节点的两条边分别标记为0,1,树的叶子节点就表示一个字符,而从根节点到叶子节点的路径上的01序列就是该字符的编码。
通过Huffman算法,能够构造出满足非前缀编码的编码方式,并且能够将文件的大小压缩到最小。
Huffman算法也是迭代进行的,令 C 表示所有字符的集合,选择出现频率最低的两个字符 \(c_i, c_j\),创造一个新的节点 c 作为这个节点父节点,并且令 c 的出现频率为这两个子节点出现频率之和。然后从集合 C 中移除节点 \(c_i, c_j\),并加入节点 c。重复这样的步骤,直到集合 C 只包含一个根节点。

上图为Huffman算法的伪代码。
下面看一个例子,假设一个文件由字符 'a', 'b', 'c', 'd', 'e' 组成,并且假设每个字符出现的频率分别为:f(a) = 20, f(b) = 7, f(c) = 10, f(d) = 4, f(e) = 18,找到一种编码方式使文件的大小压缩到最小。
使用Huffman算法可以构造出如下的完全二叉树:
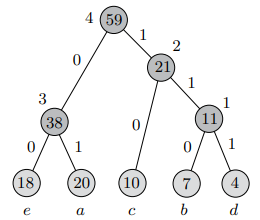
从图中可以看出每个字符的编码:e(a) = 00, e(b) = 111, e(c) = 10, e(d) = 110, e(e) = 01,这样的变长编码能够满足非前缀编码限制,所以也不存在二义性,能够被正确解码。
如果使用固定长度的编码方式,那么每个字符至少需要3比特才能编码,那么文件的长度也就是 3*(20 + 7 + 10 + 4 + 18) = 177 bits;如果使用这里得到的编码方式进行编码,那么文件的长度就是 2 * 20 + 3 * 7 + 2 * 10 + 3 * 4 + 2 * 18 = 129 bits,这样可以将文件压缩27%。

