动态规划法
算法导论
这个文档是学习“算法设计与分析”课程时做的笔记,文档中包含的内容包括课堂上的一些比较重要的知识、例题以及课后作业的题解。主要的参考资料是 Introduction to algorithms-3rd(Thomas H.)(对应的中文版《算法导论第三版》),除了这本书,还有的参考资料就是 Algorithms design techniques and analysis (M.H. Alsuwaiyel)。
动态规划法
动态规划(Dynamic Programing)和分治法一样,通过合并子问题的解决结果来解决当前的问题。
前面已经介绍过,分治法是通过将问题拆分成若干个不相交的子问题,然后递归解决这些子问题,最后再将子问题的解决结果合并成原问题的解决结果。
与之相比,动态规划则是当子问题存在重叠部分的时候使用的,也就是说当若干个子问题(subproblems)都有一个共同的子子问题(sub-subproblems)的时候,分治法就没必要再使用了,因为这种情况下分治法会重复地解决同一个子子问题,所以这个时候就需要动态规划来解决。
需要注意的是,无论是分治还是动态规划,其子问题都必须是可以独立求解的,也就是说后面的子问题的解不会依赖前面的子问题的解。
动态规划对同一个子子问题只会解决一次,并且会将解决结果存放在一个表中,从而避免重复计算同一个子子问题。
动态规划通常用于最优解(更确切地说是全局最优解)问题,也就是说当前的问题可以有很多中解决方案,而每一个解决方案都有一定的值(或者说是收益),而我们希望能找到收益最大化的解决方案,并且将这样的解决方案称为最优解。
动态规划一般分为下面四个步骤:
- Characterize: 刻画一个最优解的结构特征
- Define: 递归定义最优解的值
- Compute: 计算最优解的值,通常采用自底向上的方法
- Construct: 利用计算出的信息构造一个最优解
这里介绍一个切割钢条(Rod cutting)的例子:假设现在有一个长度为n的钢条,现在要对其进行切割,钢条的价格与钢条的长度并不是线性相关的,比如:
| Length | Price |
|---|---|
| 1 | 1 |
| 2 | 5 |
| 3 | 8 |
| 4 | 9 |
| 5 | 10 |
现在问如何切割这跟钢条?使其能够买到最高的价格。
首先是要刻画最优解的结构特征,并递归定义最优解的值。
那么现在有一个问题就是:第一次切割应该如何切割才能让其收益最大化?
假设第一次切割后将钢条分为长度分别为 i 和 n-i 的两段钢条,那么这个时候钢条的收益可以记为:
\(S(n) = p(i) + r(n-i)\)
其中 S(n) 代表长度为 n 的钢条的此时的收益,p(i) 代表长度为 i 的钢条的直接售价,r(n-i) 代表长度为 n-i 的钢条的最大收益。
那么显然,长度为 n 的钢条的最大收益应该表示为:
\(r(n) = \max_{i = 1, \dots n}(p(i)+ r(n-i))\)
接下来的步骤就和分治思想比较相似了。
但是有一个需要注意的点是,在这个问题中,每个子问题之间是存在重叠的。比如在 r(n-1) 这个子问题中,包含的子问题有 r(n-2), r(n-3), ...,而在同一个递归层次的另一个子问题 r(n-2) 中,包含的子问题有 r(n-3), r(n-4), ...。
因为子问题之间的重叠性,所以在动态规划中通常采用自底向上的递归思路,并且还需要采用一个“备忘录”来避免重复计算同一个子子问题。例如在上面的这个例子中,可以使用一个长度为 n 的全局数组来保存每个子问题的解 即 r(i) 。
最大公共子序列
这里将要介绍另一个例子,并且将通过这个例子介绍最优子结构性质与子问题重叠性质,这两个性质是动态规划中的两个关键的概念,通常能够使用动态规划解决的问题都具备这两种性质。
最大公共子序列问题,给定两个字符串 A 和 B,长度分别为 n 和 m,字母表记为 \(\Sigma\),确定两个字符串的最大公共子序列,这里的最大公共子序列的定义是,只考虑子序列的顺序而不需要考虑子序列中的字符是否是相邻的。
比如给定两个序列,A = zxyxyz,B = xyyzx,那么他们的最大公共子序列就是 xyyz。
最简单的方法是使用暴力破解法:枚举字符串 A 的所有子序列,一共有 \(2^n\) 个子序列。然后在字符串 B 中逐个搜索这些子序列,搜索每个子序列需要进行 m 次比较,能够搜索到的最大的子序列就是最大公共子序列, 那么这种方法的时间复杂度就是 \(O(m 2^n)\) ,这是个指数增长的时间复杂度。
动态规划方法是基于递归的方法,因此,用使用动态规划的方法解决这个问题就需要找到解决这个问题的递归式。
令 \(L[i,j]\) 表示序列 \(a_1,\dots, a_i\) 和序列 \(b_1, \dots, b_j\) 的最大公共子序列的长度。当这两个序列的其中或者两个都是空序列时,他们的最大公共子序列的长度为0,也就是说当 \(i = 0\) 或者 \(j = 0\) 时, \(L[i,j] = 0\)。
那么可以通过观察得出下面的结论:
- 若 \(a_i = b_j\),则\(L[i,j] = L[i - 1, j- j] + 1\)
- 若 \(a_i\ne b_j\),则\(L[i,j] = \max\{ L[i, j-1], L[i-1, j] \}\)
根据这样的规律,可以得出最大公共子序列的递归式:
递归式的思想就是,如果要得到两个序列的最大公共子序列,那么可以先计算它们的前缀的最大子序列,然后再比较这两个前缀后面的一个字符是否相同再来判断当前序列的最大公共子序列。
可以使用一个 \((n+1)\times(m+1)\) 的矩阵来保存 \(L(i,j)\) ,其中 \(0\le i \le n, 0\le j \le m\) 。
算法的伪代码如下:

可以看到这个算法的时间复杂度为 \(\Theta(nm)\).
最优子结构性质
如果一个问题是具有最优子结构性质的,那么就可以使用动态规划进行解决。或者说一个问题必须具备最优子结构性质才能够使用动态规划的方法求解。
下面演示如何证明最长公共子序列问题具有最优子结构性质。
最优子结构性质可以理解为,如果一个问题的解的结构可以拆分成子问题的解,那么子问题的解一定是这个子问题的最优解。
最优子结构性质的证明方法通常是采用反证法进行证明。
设 \(X=(x_1, ..., x_n), Y=(y_1, ..., y_m)\) 是两个序列,它们的最长公共子序列为 \(Z=(z_1, ..., z_k)\),那么:
I. 若 \(x_n = y_m\) :
则 \(z_k = x_n = y_m\),那么显然有:
\((z_1, ..., z_{k-1})\) 是 \((x_1, ..., x_{n-1})\) 和 \((y_1, ..., y_{m-1})\) 的最长公共子序列。
即\(LCS(n,m) = LCS(n-1, m-1) + 1\)
II. 若 \(x_n\ne y_m\) :
那么可以分两种种情况讨论:
i. 若 \(z_k \ne x_n\),那么可以证明 \(Z\) 是 \((x_1, ..., x_{n-1})\) 和 \((y_1, ..., y_n)\) 的最长公共子序列。
反证法,假设 \((x_1, ..., x_{n-1})\) 和 \((y_1, ..., y_m)\) 的最长公共子序列为 \(Z' = (z_1', ..., z_h')\ne Z\),那么因为 \(x_n\ne y_m, x_n\ne z_k\) 所以\(x_n\) 不会影响 \(X\) 和 \(Y\) 的最长公共子序列,因此,\(Z'\) 也是\((x_1, ..., x_n)\) 与 \((y_1, ..., y_m)\) 的最长公共子序列,而这与前提条件 \(Z\) 是 \((x_1, ..., x_n)\) 与 \((y_1, ..., y_m)\) 的最长公共子序列相矛盾,因此 \(Z\) 必然是 \((x_1,...,x_{n-1})\) 和 \((y_1, ..., y_m)\) 的最长公共子序列。
即 \(LCS(n,m) = LCS(n-1, m)\)
ii. 若 \(z_k\ne y_m\) ,那么同理可证 \(Z\) 是 \((x_1, ..., x_n)\) 和 \((y_1, ..., y_{m-1})\) 的最长公共子序列。
即 \(LCS(n,m) = LCS(n, m-1)\)
最终,若 \(x_n\ne y_m\),则 \(LCS(n,m) = \max\{ LCS(n-1, m), LCS(n, m-1)\}\)
综上,最长公共子序列问题具有最优子结构性质,子问题的递归结构如下:
子问题的重叠性
分治思想与动态规划思想都是具有最优子结构性质的,但是动态规划与分治的一个区别在于,动态规划解决的问题是具有子问题重叠性质的,而分治解决的问题的子问题则是不重叠的。
最长公共子序列问题的子问题重叠性如下图所示:
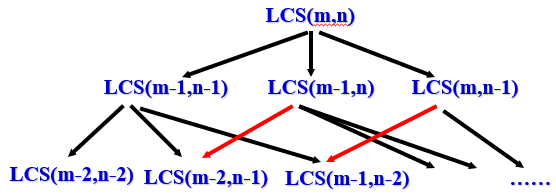
可以看到组成最优解的不同子问题的解是有一定重合的,基于这样的性质,可以减少计算次数,将其中一个子问题的解记录下来,到另一个子问题需要用到这个解是就不需要再重新计算。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号