分治法

算法导论

这个文档是学习“算法设计与分析”课程时做的笔记，文档中包含的内容包括课堂上的一些比较重要的知识、例题以及课后作业的题解。主要的参考资料是 Introduction to algorithms-3rd(Thomas H.)（对应的中文版《算法导论第三版》），除了这本书，还有的参考资料就是 Algorithms design techniques and analysis (M.H. Alsuwaiyel)。

分治法

分治法(Divide-and-Conquer)是一种十分有用的算法思想，比如归并排序所体现出来的算法思想就是分治。

在分治的算法思想下，递归性地解决问题，在每一次递归都执行下面的三个步骤：

1. Divide: 将当前的问题划分为若干的子问题，这些子问题都是同一个问题的更小的实例，或者说是更小规模的相同问题
2. Conquer: 递归性地解决子问题，也就是将子问题传到下一层递归中。如果子问题的规模已经足够小了，那么就直接解决这个子问题
3. Combine: 将子问题的解决结果合并为当前问题的解决结果

这就是分治算法的基本思想，另外，在分治思想中还涉及到两个概念：

• recursive case: 就是当问题规模太大而无法直接解决，只能用递归解决的情况
• base case: 就是当问题规模足够小，能够直接解决的情况

比如归并排序就是一种比较典型的分治思想的算法，把对一个序列的排序工作划分成对两个子序列的排序工作：

\[T(n) = \begin{cases} \Theta(1) & if\space n=1\\ 2T(n/2) + \Theta(n) & if\space n>1 \end{cases} \]

即，如果序列的长度为1，那么就无需排序，需要的时间复杂度为\(\Theta(1)\)，而如果序列的长度大于1，那么就这个序列划分为两个子序列，并且对子序列进行排序，然后将排好序的子序列进行合并，合并两个有序的子序列需要的时间复杂度为\(\Theta(n)\)。

而上面的式子也被称为递归式。

递归式求解

下面介绍如何求解递归式，也就是通过递归式计算算法整体的时间复杂度的方法：

比如说有下面这样的一个递归式：

\[T(n) = \begin{cases}d & if\space n=1\\ aT(n/b) + f(n) & if\space n>1\end{cases} \]

在这个式子中，原问题被分解为a个子问题，每个子问题的规模为原来的 1/b 倍，而将这个a个子问题的解合并成原问题的解需要的时间为f(n)，而解决一个base case所需的时间为常数d。

最容易想到的方法就是对递归式进行展开：

\[\begin{align} T(n) &=aT(\frac{n}{b}) + f(n)\\ T(\frac{n}{b})&=a(\frac{n}{b^2}) + f(\frac{n}{b})\\ \cdots\\ T(n)&=a^kT(\frac{n}{b^k})+\sum_{i=0}^{k}a^if(\frac{n}{b^i}) \end{align} \]

不过这样的方法比较抽象，可能需要分很多种情况进行讨论。

在 Introduction to algorithm 一书中，介绍了三种求解递归的方法，

• substitution method：猜测一个界限，然后使用数学归纳法来证明这个猜测是正确的
• recursive-tree method：使用递归树来，递归树中的节点表示在递归的各个级别上产生的成本，然后使用边界求和的方法来求解
• master method：可以用于计算形如\(T(n) = aT(n/b) + f(n)\)形式的递归式的边界，在这个式子中，原问题被分解为a个子问题，每个子问题的规模为原来的 1/b 倍，而将这个a个子问题的解合并成原问题的解需要的时间为f(n)

substitution method通常用于证明渐进上界和渐进下界，当然也可以用于证明紧渐进界。

这里介绍一个使用substitution method方法求解递归式的例子，递归式如下：

\[f(n) = \begin{cases} d & if\space n = 1\\ f(\lfloor n/2\rfloor)+f(\lceil n/2 \rceil) + bn & if\space n\ge 2 \end{cases} \]

对于非负常数 b 和 d，如果 n 为2的整数幂，那么这个递归式可以简化为：

\(f(n) = 2f(n/2) + bn\)

那么我们可以假设:

\(f(n) \le cbn\log n + dn\)，其中 c 为大于0的常数，并且接下来将会确定 c 的值。

这部分的内容主要摘自 Algorithms design techniques and analysis，这里介绍了一些推论，用于假设递归式的边界，但是这里由于篇幅限制，所以没进行介绍。

假设上面猜测的结果在\(n\ge 2\)时，对于\(\lfloor n/2 \rfloor\)和\(\lceil n/2 \rceil\)是成立的，那么我们将其带入原式子右边的子式子可得：

\[\begin{align} f(n) = & f(\lfloor n/2 \rfloor) + f(\lceil n/2 \rceil) + bn\\ \le & cb\lfloor n/2 \rfloor\log (\lfloor n/2 \rfloor) + d\lfloor n/2\rfloor + cb\lceil n/2 \rceil\log (\lceil n/2 \rceil) +d\lceil n/2 \rceil + bn\\ \le&cb\lfloor n/2 \rfloor\log (\lceil n/2 \rceil) + cb\lceil n/2 \rceil\log (\lceil n/2 \rceil) + dn + bn\\ =&cbn\log(\lceil n/2 \rceil) + dn + bn\\ \le&cbn\log ((n+1)/2) + dn + bn\\ =&cbn\log (n+1) - cbn + dn + bn \end{align} \]

欲使前面的假设成立，则有：

\[\begin{align} cbn\log (n+1) - cbn + dn + bn \le& cbn\log n + dn\\ cbn\log(n+1) - cbn + bn \le& cbn\log n\\ c\log (n+1) -c + 1\le& c\log n\\ c\ge& \frac{1}{1 + \log n - \log(n+1)} = \frac{1}{1 + \log\frac{n}{n+1}} \end{align} \]

当 \(n\ge 2\)时，

\(\frac{1}{1+\log\frac{n}{n+1}} \le \frac{1}{1+\log\frac{2}{3}} \lt 2.41\)

于是取c = 2.41。并且当n = 1时，\(f(n) = d\le cb\log 1 + d = d\)，假设依然成立。

所以能够求解出上面递归式的上界为：\(f(n)\le 2.41 bn\log n + dn\)

现在计算递归式的渐进下界，同样，假设递归式\(f(n)\)的下界为\(cbn\log n + dn\)，其中 c 为大于0的常数，后面会确定其取值。

假设上面的猜测在\(n\ge 2\)时，对于\(\lfloor n/2 \rfloor\)和\(\lceil n/2 \rceil\) 是成立的，那么带入递归式右边可得：

\[\begin{align} f(n)=&f(\lfloor n/2 \rfloor) + f(\lceil n/2 \rceil) + bn\\ \ge&cb\lfloor n/2 \rfloor\log(\lfloor n/2 \rfloor) + d\lfloor n/2 \rfloor + cb\lceil n/2 \rceil\log(\lceil n/2 \rceil) + d\lceil n/2 \rceil + bn\\ \ge&cb\lfloor n/2 \rfloor\log(\lfloor n/2 \rfloor) + d\lfloor n/2 \rfloor + cb\lceil n/2 \rceil\log(\lfloor n/2 \rfloor) + d\lceil n/2 \rceil + bn\\ =&cbn\log (\lfloor n/2 \rfloor) + dn + bn\\ \ge&cbn\log(n/4) + dn +bn\\ =&cbn\log n - 2cbn + dn + bn \end{align} \]

欲使上面的假设成立，则有：

\[\begin{align} bn - 2cbn &\ge 0\\ c&\le \frac{1}{2} \end{align} \]

于是取 \(c =\frac{1}{2}\)，则当\(n\ge 2\)时，\(f(n)\ge \frac{1}{2} bn\log n + dn\) 成立，并且当\(n= 1\)时，\(f(n) = d \ge \frac{1}{2}b\log 1 + d =d\)，假设依然成立。

所以能够求出上面的递归式的下界为：\(f(n)\ge \frac{1}{2}bn\log n + dn\)

综上，上述递归式的紧渐进边界为\(f(n) =\Theta(n\log n)\)

这种方法的困难在于提出一个巧妙的猜测，将这个猜测作为递归式的严格边界。然而，在多数情况下，给定递归式类似于另一个递归式，而这个递归式的解是已经提前知道了的，所以可以借助这个递归式的解，来假设当前递归式的解，上面介绍的这个例子就是这样的。

在上面的这个三个方法中，最常用并且也是最有用的方法就是主方法(master method)，这个方法通常用于计算递归式的渐进边界。

主定理

主定理主要用于求解下面这种形式的递归式：

\(T(n)=aT(n/b) + f(n)\)

其中a, b是大于等于1的常数，而 f(n) 是一个渐进的正函数。

将T(n)分下面三种情况进行讨论：

• 若 \(f(n) = O(n^{\log_b a-\epsilon})\)，其中 \(\epsilon \gt 0\)，则 \(T(n)=\Theta(n^{\log_b a})\)
• 若 \(f(n)=\Theta(n^{\log_b a})\)，则 \(T(n)=\Theta(n^{\log_b a}\lg n)\)
• 若 \(f(n)=\Omega(n^{\log_b a +\epsilon})\)，其中 \(\epsilon \gt 0\)，并且如果 \(af(n/b) \le cf(n)\)，对于大于1的常数 c 以及足够大的 n 满足，则 \(T(n)=\Theta(f(n))\)

下面介绍一些使用主定理求解递归式的例子：

# 1. \(T(n) = 9T(n/3)+n\)

则: \(n^{\log_ba} = n^{\log_3 9}=n^2\)

\(f(n)=n=O(n^{\log_39 -\epsilon})\)，其中\(\epsilon =1\)

根据主定理的第一个情况，\(T(n)=\Theta(n^2)\)

# 2. \(T(n)=T(2n/3)+1\)

则: \(n^{\log_ba}=n^{\log_{3/2}1} = 1\)

\(f(n) = 1 = \Theta(1)\)

根据主定理的第二个情况，\(T(n)=\Theta(n^{\log_{3/2}1}\lg n) = \Theta(\lg n)\)

# 3. \(T(n)=3T(n/4)+n\lg n\)

则: \(n^{\log_b a} = n^{\log_43} = O(n)\)

\(f(n) = n\lg n = \Omega(n^{\log_43+\epsilon})\)，其中\(\epsilon = 1 - \log_43\approx 0.2\)

所以可以应用主定理的第三种情况。

而\(af(n/b) = 3(n/4)\lg(n/4) = (3/4)n\lg(n/4) \le (3/4)n\lg n = cf(n)\)，其中 \(c = 3/4\)

根据主定理的第三种情况，\(T(n) = \Theta(n\lg n)\)

Selection Problem

选择问题(Selection Problem)：找到一个大小为 n 数组中的第 k 小的元素。

那么最直接的方法是，先将这个数组进行排序，然后取第 k 个元素，那么这样的方法的时间复杂度为\(\Omega(n\log n)\)，这也是所有基于比较的排序算法在最坏情况下的时间复杂度。

然而事实上，找到第 k 小的元素可以有线性时间复杂度的最优解。因为一个最简单的道理是，如果对原数组进行了排序，那么我们不仅能够找到第 k 小的元素，我们也能找到第 k+1 小的元素等，所以对数组进行排序的操作存在着一些冗余的工作量。

下面介绍这个问题最优解法的思路：

- 如果数组中的元素数量小于44个（44是一个预定义的阈值，后面会解释为什么会将这个阈值），那么就直接对数组进行排序，然后找第 k 个元素

- 否则，找到这个数组比较靠近"中间"的元素记为 mm，然后通过下面的方法将数组划分为三组：

- $A_1=\{a|a \lt mm\}$
- $A_2=\{a|a=mm\}$
- $A_3=\{a|a\gt mm\}$

那么，可以分下面几种情况讨论：

\#1. 若$|A_1| \ge k$，那么数组中第 *k* 小的元素必然在集合 $A_1$中，继续在 $A_1$ 中找第 *k* 小的元素

\#2. 若$|A_1| \lt k, |A_1| + |A_2|\ge k$，那么数组中第 *k* 小的元素就在 $A_2$ 中，所以第 *k* 小的元素就是 *mm*

\#3. 若$|A_1 + A_2| \gt k$，那么数组中第 *k* 小的元素必然在 $A_2$ 中，继续在$A_2$ 中找第 $k - |A_1| - |A_2|$ 小的元素

下面将介绍如何找到数组中靠近"中间"的元素：

将这个数组中每5个元素分为一组，如果数组长度不能被5整除，那么就丢弃剩下的元素。

找到每个小组的中位数，将这些中位数放在一个集合中，这个集合记为m，那么我们要找的元素 mm 就是集合 m 的中位数。

算法伪代码如下：

下面通过一个例子来演示这个算法的过程，并且为了方便演示而取消了阈值判断过程：

假设数组 A = { 8, 33, 17, 51, 57, 49, 35, 11, 25, 37, 14, 3, 2, 13, 52, 12, 6, 29, 32, 54, 5, 16, 22, 23, 7 }

要找到数组A中的第13小的元素，也就是数组A的中位数。

先将A五五分组：

(8, 33, 17, 51, 57), (49, 35, 11, 25, 37), (14, 3, 2, 13, 52), (12, 6, 29, 32, 54), (5, 16, 22, 23, 7)

然后找到每个小组的中位数（注意到这里每个小组只有5个元素，所以找中位数的时间开销可以视为一个固定常数），并且放入集合中：M={ 33, 35, 13, 29, 16 }

对 M 排序，M={ 13, 16, 29, 33, 35 }，则 mm = 29

现在对原数组 A 进行划分：

\(A_1=\{ 8, 17, 11, 25, 14, 3, 2, 13, 12, 6, 5, 16, 22, 23, 7 \}\)

\(A_2=\{ 29 \}\)

\(A_3=\{ 33, 51, 57, 49, 35, 37, 52, 32, 54 \}\)

因为\(|A_1| = 15 > 13\)，所以丢弃\(A_2,A_3\)，在\(A_1\) 中找第13小的元素。

令 \(A = A_1\) 并五五分组：

(8, 17, 11, 25, 14), (3, 2, 13, 12, 6), (5, 16, 22, 23, 7)

找到每个小组的中位数，并且放入集合中：M = { 14, 6, 16 }

则 mm =14

现在对数组 A 进行划分：

\(A_1=\{ 8, 11, 3, 2, 13, 12, 6, 5, 7 \}\)

\(A_2=\{14\}\)

\(A_3=\{ 17, 25, 16, 22, 23 \}\)

因为\(|A_1| + |A_2| = 10 < 13\)，所以丢弃\(A_1, A_2\)，在\(A_3\) 中找第13-10=3小的元素

显然\(A_3[3]=22\)

所以原数组第13小的元素为22。

Algorithm analysis

显然，不难验证上面算法的正确性。

现在来分析上面这个算法的时间复杂度。

想要分析出分治算法的时间复杂度，那么就需要先确定其子问题的大小，如下图：

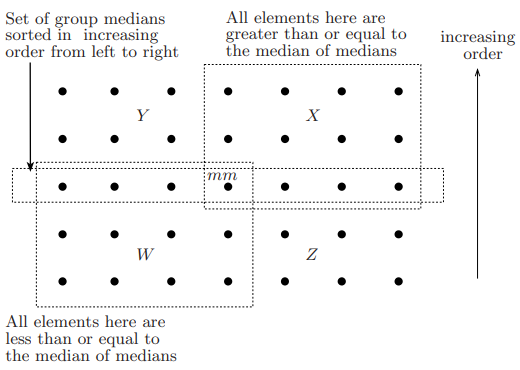
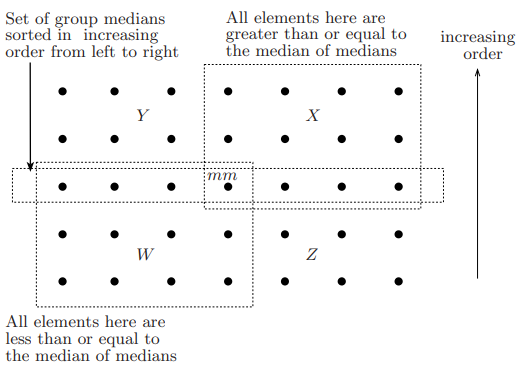
上图中，所有元素每列是按照从下往上递增排序的，然后将每列按照该列中位数的大小从左到右递增排序，那么对于整个集合的中间数 mm，图中左下角(W)的元素都是小于或等于 mm 的元素，图中右上角(X)的元素都是大于或等于 mm 的元素。

而这个算法中的子问题规模是所有严格小于中间数 mm 的元素集合( A1 )大小，或者严格大于中间数 mm 的元素集合( A3 )大小。现在考虑所有小于或等于中间数 mm 的集合( A1' )，显然，这个集合至少是和集合 W 一样大的。即：

\(|A1'| \ge 3\lceil \lfloor n/5 \rfloor / 2 \rceil \ge \frac{3}{2}\lfloor n/5 \rfloor\)

那么所有严格大于中间数 mm 的元素集合就是所有小于或等于中间数 mm 的元素集合的补集，即：

\(|A3| \le n - \frac{3}{2}\lfloor n/5 \rfloor \le n - \frac{3}{2}(\frac{n-4}{5}) = n - 0.3n + 1.2 = 0.7 n + 1.2\)

同理可得：

\(|A1| \le n - \frac{3}{2}\lfloor n/5 \rfloor \le n - \frac{3}{2}(\frac{n-4}{5}) = n - 0.3n + 1.2 = 0.7 n + 1.2\)

现在可以开始计算整个算法的时间复杂度了：

首先整个集合的规模( n )是知道的；将整个集合五五分组的时间复杂度是\(\Theta(n)\)；将每组的 5 个元素进行排序的时间复杂度是 \(\Theta(n)\)，因为对 5 个元素排序最多只需要 7 步，可以视为一个常数开销；找到所有中位数的中位数的开销是 \(T(\lfloor n/5 \rfloor)\)，使用这里的选择算法找中位数；在确定了中间数 mm 后，就可以进入子问题了，根据前面的分析，子问题的时间复杂度应该是 \(T(0.7n + 1.2)\)。即：

\(T(n) = T(\lfloor n/5 \rfloor) + T(0.7 n + 1.2) + cn\)

其中 c 为足够大的常数。

为了将 0.7n+1.2 转换成n的常数倍形式，这里假设:

\(0.7n + 1.2 \le \lfloor 0.75n \rfloor\)

当 \(n = 44\)时，\(0.7n + 1.2 \le 0.75n - 1\) 成立。

因此，算法的时间复杂度为:

\[T(n) = \begin{cases} c& n \lt 44\\ T(\lfloor n/5 \rfloor) + T(\lfloor 3n/4 \rfloor) + cn &n\ge 44 \end{cases} \]

因为 \(\frac{1}{5} + \frac{3}{4} < 1\)，所以算法的时间复杂度为 \(T(n) = \Theta(n)\)。