算法分析
算法导论
这个文档是学习“算法设计与分析”课程时做的笔记,文档中包含的内容包括课堂上的一些比较重要的知识、例题以及课后作业的题解。主要的参考资料是 Introduction to algorithms-3rd(Thomas H.)(对应的中文版《算法导论第三版》),除了这本书,还有的参考资料就是 Algorithms design techniques and analysis (M.H. Alsuwaiyel)。
算法分析
在设计一个算法的时候,能够衡量,或者说至少能够做出有根据的陈述,算法的时间和空间复杂度是十分重要的。因为这样能够让我们从对某一个问题的多种可选解决方案中选择更好的一种,或者确定某种解决方案能够满足当前问题下的资源限制的要求。
在衡量时间复杂度的时候,想要预测出绝对运行时间是不现实的。因为算法运行的时间由很多因素决定,比如实现算法的编程语言,运行算法的机器,以及该机器上同时运行的其他的程序等。
因此,我们需要一种机器无关的概念(Machine-independent notion)来衡量算法的运行时间。
所以当前的算法分析主要是衡量算法的相对运行时间,也就是说当某个算法接收了一个长度为 n 的输入后,那么这个算法的相对运行时间就是达成完成输出所需要的抽象操作(Abstract Operations)的次数,我们以一个包含 n 的函数来表示这个算法的相对运行时间。
比如下面的这个例子:
for(int i = 0; i < a.length; i++){
System.out.println(a[i]);
}
这个算法接收的输入的长度为 n = a.length 是一个固定长度的输入,那么这个算法达成输出所需要的操作次数就为:
- 1 次变量 i 的初始化
- n 次 i 与 a.length的比较
- n 次 i 的增量计算
- n 次数组下标计算(to compute a[i])
- n 次调用函数 "System.out.println()" 的操作
所以这个算法的相对运行时间可以记为:T(n) = 4n + 1
但是在上面的计算中,每个操作所需的时间其实是并不相等的,比如比较操作和函数调用操作所需的时间明显是不同的。而调用函数需要的时间也是远远大于增量、比较和索引操作需要的时间,所以不妨把这些操作简化为一个操作,即"比较-索引-打印-增量"操作。那么这样的话,这个算法的时间复杂度就为:T(n) = n + 1。显然,一次初始化所需的时间并不是那么重要,所以可以进一步简化为:T(n) = n。
需要注意的是,这里之所以能够将算法的复杂度简化为 n ,是因为相较于打印操作,其他操作所花费的时间都是可忽略的。
这里记录一下我曾经在编程作业(C language)中犯的一个错误:假设 a 是一个字符串,其长度记为 n,现在要打印出这个字符串中的每一个字符。
for(i = 0; i < strlen(a); i++) printf("%c ", a[i]);那么这种情况下,算法的时间复杂度就应该是T(n) = 2n,因为在比较操作中调用了函数"strlen()",这个函数会遍历整个字符串直到遇到 '\0' 才能计算出字符串的长度,所以每次比较操作都需要 n 次数组索引操作和比较操作。
所以这个时候的算法的时间复杂度为:T(n) = \(n^2 + n\)
这里的时间复杂度T(n) = n,有时候也可以记为\(\lambda n.n\),即大小为n的输入,需要进行n次操作。
这里再介绍一个比较有趣的例子,计算两个方阵相乘(Multiply two square matrices)的结果:
给定两个方阵A, B,这两个方阵以二维数组的形式存储即 a[n][n], b[n][n],然后输出一个新的矩阵c[n][n]。
那么根据矩阵相乘的规则,可以得到下面的算法来计算两个矩阵相乘的结果:
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
double sum = 0;
for(int k = 0; k < n; k++)
{
sum += a[i][k] * b[k][j];
}
c[i][j] = sum;
}
}
从里向外看:
在k-loop中,一共有1次初始化以及n次循环,每次循环中有1次比较,1次递增,4次数组索引,1次乘法,1次加法以及1次赋值;
在j-loop中,有1次初始化,n次比较,n次递增,n次初始化,n次k-loop,n次赋值;
那么这是否意味着:T(j-loop) = n * (T(k-loop) + 4) + 1?
其实不然,因为相对于k-loop,其他的操作所花费的时间并不重要,所以通过类似的观点,我们可以忽略所有简单的for循环中的初始化、测试和递增操作。而在这个例子中,我们只需要考虑 sum += a[i][k] * b[k][j] 操作的次数,因为相比于其他操作,这个操作所需要的时间明显使更多的。
所以这个算法的时间复杂度就是:T(n) = \(n^3\)
但是,这里的 n 为输入的宽度,而不是输入的规模,真正的输入规模应该是\(2n^2\)
如果以输入规模来考虑这个算法的时间复杂度的话,那么得到的结果就与前面以输入的宽度来考虑的时间复杂度结果不一样了。
所以我们令 N = \(2n^2\),那么T(N) = \(N^{1.5}\)
因此,使用不同的方法来衡量输入的大小,也会得到不同的结果。
再介绍一个例子,找到数组中某一个元素的位置:
for(int i = 0; i < a.length; i++)
{
if(a[i] == x)
{
return Optional.of(i);
}
}
return Optional.empty();
那么这种场景下就需要分情况讨论了,比如最好的情况下,x = a[0],那么B(n) = 1,最坏的情况下,x不在数组a中,那么W(n) = n。
那平均的时间复杂度是多少呢?这个其实就很难判断的,因为想要知道这个算法的平均时间复杂度,那么首先需要知道这些元素的期望分布。
到目前为止,我们可以分析一个算法的时间复杂度,将该算法的时间复杂度表示成一个与输入规模 n 相关的函数,但是如何通过比较时间复杂度函数来比较哪个算法更加优秀呢?
所以,我们可以将算法的时间复杂度按照其"增长率"对其进行分类,比如:
- 常数增长:时间复杂度是一个常量,即无论输入的规模如何,算法都只需要进行固定次数的操作,比如\(\lambda n.1\)
- 对数增长:时间复杂度是一个对数函数,即需要的操作次数与输入规模的对数成比例,比如\(\lambda n.\log n\)
- 多项式增长:时间复杂度是一个多项式,即需要的操作次数是输入规模的一个多项式,比如\(\lambda n.n^k, k\ge 1\)
- 指数增长:时间复杂度是一个指数函数,即需要的操作次数是输入规模的指数,比如\(\lambda n.c^n,c>1\)
所以,一般是通过算法时间复杂度的增长率来比较不同算法的性能的,但是函数的增长率依然的表示依然还是一个以 n 为变量函数,所以为了更方便比较不同函数的增长率通常会使用渐进的方法进行比较,比如一个函数可能会收敛于某个上界或者下界,然后我们就可以通过该函数收敛的上界与下界来比较不同的函数。
When we look at input sizes large enough to make only the order of growth of the running time relevant, we are studying the asymptotic efficiency of algorithms. That is, we are concerned with how the running time of an algorithm increases with the size of the input in the limit, as the size of the input increases without bound. Usually, an algorithm that is asymptotically more efficient will be the best choice for all but very small inputs.
-- Introduction to algorithms
如果对时间复杂度的增长率进行了衡量,那么我们通常会忽略掉
- all but the "largest" term, and
- any constant multipliers
比如:\(\lambda n.0.4n^5 + 3n^3 + 254\) 的渐进表示就为 \(n^5\),只保留的最大的一项,并且忽略掉所有的常数倍数。
之所以会进行这样的忽略是因为下面的原因:
- 6n 和 3n 之间的差距其实是没有意义的,因为在一个运行速度是两倍的计算机上,可以让时间复杂度为 3n 的算法所花费的时间和在一个普通运行速度的计算机上的运行的时间复杂度为 6n 的算法所花费的时间一样;
- 2n 和 2n + 8之间的差距也是可忽略的,因为 n 可能会变得越来越大;
- 如果比较 \(\lambda n.n^3\) 和\(\lambda n.kn^2\)的增长率,那么无论 k 取多大,总会存在一个N,使得\(\forall n > N, n^3 > kn^2\)
那么我们应该如何对时间复杂度的渐进表示进行形式化的表达?也就是如何能够通过一种形式化的方法找到一个时间复杂度表达式的渐进表示,比如\(T(n) \in\) {the set of all quadratic functions}
Big-O: 渐进上界
Def. 称一个函数 f 属于 O(g) ,即\(f \in O(g)\),当且仅当,存在常数 c 和 N 能够满足 \(\forall n \gt N, f(n)\)的上界为\(g(n)\)的常数倍,即:
比如:\(\lambda n.0.4n^5 + 3n^3 + 253\in O(\lambda n.n^5)\)
为了简化,一般会丢弃Big-O中的lambda, 比如上面的这个例子就可以写成\(O(n^5)\)。
渐进上限能够让我们丢弃掉时间复杂度表达式中的较小的项以及常数因子。
比如:证明,\(7n^4 + 2n^2+n+20\in O(n^4)\),
所以我们可以取常数 \(c=30, N=1, \forall n \gt N,7n^4 + 20n^2 +n + 20 \lt c*n^4\)
当输入的规模 n 比较大的时候,Big-O渐进上限是比较有用的。
但是对于比较小的输入规模 n,Big-O中舍弃低阶项和常数因子的方法就存在误导性,比如下面的函数:
\(0.00001n^5 + 10^6 n^2\)
当 n 比较小的时候如果将上面的函数的渐进表达为\(O(n^5)\) 就不太恰当。
如果比较下面两个时间复杂度:
\(8n\log n\) and \(0.01n^2\)
会发现如果 n < 10701,那么前者是比后者更大的。
还需要注意的是,Big-O只是上限,而不是严格的上限。如果说一个函数属于\(O(n^2)\),那么这个函数也属于\(O(n^3)\), \(O(n^{100})\)或者\(O(2^n)\)。
Big-\(\Omega\): 渐进下界
Def. 称一个函数 f 属于 \(\Omega(g)\) ,即\(f\in \Omega(g)\),当且仅当,存在常数 c 和 N 能够满足 \(\forall n \gt N, f(n)\)的下界为\(g(n)\)的常数倍,即:
渐进下界是十分有用的,因为渐进下界能够表示这个算法的执行至少需要这么多的时间。
比如前面的打印数组的例子中,我们可以说这个算法的时间复杂度属于\(O(2^n)\),因为\(2^n\)确实是这个算法时间复杂度的一个上限,但是不是一个严格的上限。但是我们也可以说这个算法的时间复杂度属于\(\Omega(n)\),因为这个算法至少需要线性的时间来执行,这样更加准确。
当然,任何算法的时间复杂度都属于\(\Omega(1)\)。
Big-\(\Theta\):紧渐进界
Def.如果一个函数的渐进上界和渐进下界是相等的,那么就可以使用Big-\(\Theta\) 的概念:
三种渐进分析的图形化表示如下图:
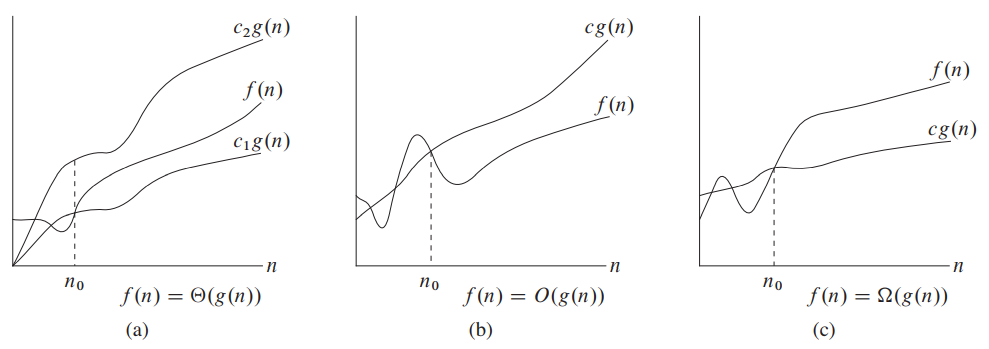
因此,我们就可以说打印数组的算法的时间复杂度属于\(\Theta(n)\)。
不是所有算法的时间复杂度都可以使用Big-\(\Theta\) 来表示,比如\(\lambda n.n^2\cos n\)就不能使用Big-$\Theta $表示,因为这个时间复杂度没有渐进下界。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号