关于对MD4差分碰撞攻击的理解
现在MD4算法已经被淘汰,现在广泛使用的hash函数主要是MD5和SHA1。但因为MD5和SHA1遵循MD4的设计思想,所以可以先理解对MD4的差分碰撞方法来理解对另外两种Hash函数的碰撞思想。
数字签名:
Hash函数,又被称为散列函数,它的作用是将任意长度的报文压缩成一个128比特的散列值(有时候也被称为报文摘要)。现在被广泛应用于数字签名技术中,而数字签名是实现安全电子交易的核心技术之一,它具有和实际签名一样的法律效应,它具有以下性质:
可验证性(verifiable):可以证明报文的发送者确实是实际的发送者,而不是其他人。
不可伪造性(unforgeable):可以证明报文没有被恶意更改。
不可抵赖性(non-repudiation):可以证明发送方确实是发送了该报文,防止其否认。
数字签名的工作流程:对即将发送的报文进行Hash函数压缩,得到一个散列值。然后使用个人的私钥对这个散列值进行加密,这个加密后的散列值就是所谓的数字签名。其中最基础的原理其实是因为每个人都有一个唯一的私人密钥并且只有自己才知道自己的私钥,所以可以通过这个私人密钥进行身份验证。但是如果直接对即将发送的报文使用私钥加密的话,由于报文可能会很大,所以会降低通信的效率,而且加密的计算量会很大会花费很多时间。
Hash函数的安全性质:
所以在网络中涉及身份验证时,报文通常都是以其散列值的形式出现的。这样我们就必须要求Hash函数具有下面这些安全性质:
弱无碰撞:给定一个x,对于任意的y,y != x。计算上无法得到h(x)=h(y)。
强无碰撞:对于任意的一对数x,y,y != x。计算上无法得到h(x)=h(y)。
注意到这里所强调的“计算上无法得到”,其实这个道理很简单,就好比“367个同一年出生的人中必然有两个人在同一天出生”一样。可以考虑这样的函数:f:A→B,A代表所有报文的集合,而B代表所有散列值的集合。因为报文是“任意的”,所以|A|=∞。而散列值只有128位,所以|B|=2128。因为|A|>|B|,所以 f 不是一个单射函数,所以必然有至少两个报文有相同的散列值。而这里之所以强调“计算上无法得到”,其实就是排除通过枚举寻找碰撞报文的方法。
MD4算法的以及碰撞原理的理解:
要掌握MD4算法的差分碰撞攻击方法,首先要对MD4有一定的了解,下面这个链接有对MD4算法的详细解释。
https://tools.ietf.org/html/rfc1186
其实我个人对MD4算法的理解就是:message + initial_chainvalue ---MD4---> Hash_value。
通过对MD4算法的了解可以得知:每次生成的散列值都伴随着48个链接变量(不包括4个初始的链接变量),可以把这48个链接变量想象成散列值的生成路径。每个报文与其路径都指向一个唯一的散列值,所以现在想要让另外一个不同的报文与原来的报文有着相同的散列值,则需要从路径下手。也就是说,我们目的是要让碰撞的报文按照经过计算后的路径最终生成与原报文相同的散列值,称这个路径为差分路径。这个差分路径的产生依赖于两个因素:一是报文的差分,另外一个就是把这个路径代入MD4算法中可以生成和原报文一样的散列值。
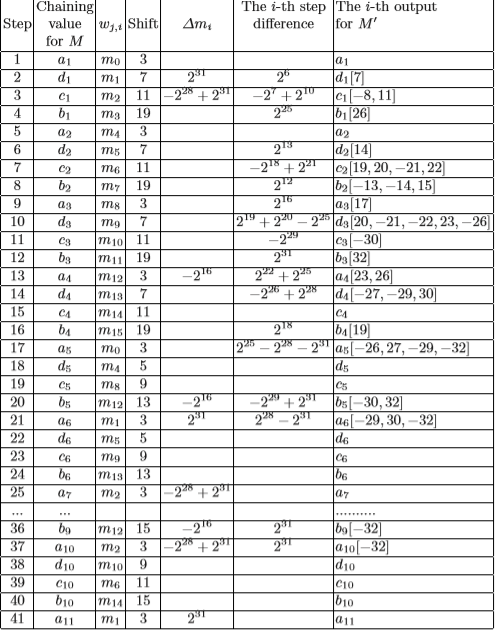
这张表中最右边那列的值,就是所谓的差分路径\((a_1,d_1[7],c_1[-8,11],b_1[26]...)\),这些链接变量是由通过差分生成的消息生成而来的,与原来的路径\((a_1,d_1,c_1,b_1…)\),即原消息生成的链接变量不同,但这两条链接变量最终都生成了相同的散列值,于是就发生了碰撞。
关于碰撞路径的理解:
本来按照给定的定义来看的话,碰撞报文产生\(d_1[7]\)的意思是:碰撞报文产生的d1是原报文产生的\(d_1\)在从低到高的第7位发生了由0变为1的变化。这个看上去好像是一个位上的变化。但实际上,但实际上之前的一些寻找碰撞的算法是通过异或运算来构造碰撞报文的,而王小云教授的攻击方法的思想则是通过差分来构造报文的,也就是说是通过加减运算来构造碰撞报文的。
所以,\(d_1[7]\)事实上应该理解为:差分报文产生的\(d_1'\),原报文产生的\(d_1\),\(d_1'=d_1+2^6\)。换句话说,\(d_1[7]=d_1+2^6\)。
不难看出,这与之前定义所给出的说法有些许不同,因为如果原报文产生的\(d_1\)在第7位上是1,那么\(d_1+2^6\)就不能表述成\(d_1\)在第7位发生了从0变为1的变化了。因为如果\(d_1\)的第7位是1,那么加上\(2^6\)后,会影响直到前面第一个值为非1的位。实际上,这就是我们所说的差分扩散,本来加在第7位上的值,影响了前面几个位的值。
那么,为了使\(d_1[7]=d_1+2^6\)。我们需要对\(d_1\)添加一定的条件,只有当\(d_1\)满足这个条件后,\(d_1[7]\)才能等于\(d_1+2^6\)。而这就涉及到对原报文链接变量的条件限制了。
关于原报文链接变量的限制条件的理解:
并不是所有的报文,都能够通过在消息字中加上上表中所给出的差分( Δmi )来找到碰撞报文。我们需要找到满足条件的报文,它满足这样的条件:它所产生的链接变量都能够满足下面这些限制:

前面提到过,必须使原报文产生的链接变量满足某个条件,才能使\(d_1[7]=d_1+2^6\)。显而易见,这里我们要加的条件就是\(d_{1,7}=0\)。以此类推,我们为了使碰撞路径等于原报文加上相应的差分,就需要给出相应限制条件。这样我们就能得出一部分限制条件了。
而另外一部分限制条件的推导,则依赖于MD4算法中布尔函数的性质了。

这里以第一轮算法中的前四个链接变量的推导为例:
\(a_1'=(a_0+F(b_0,c_0,d_0)+m_0)<<<3\)
\(a_1'=a_1\)不需要任何条件
\(d_1'=(d_0+F(a_1,b_0,c_0)+m_1+2^{31})<<<7\)
\(d_1'=d_1[7]\)的条件是\(d_{1,7}=0\)
\(c_1'=(c_0+F(d_1[7],a_1,b_0)+m_2-2^{28}+2^{31})<<<11\)
\(c_1'=c_1[-8,11]\)的条件是\(c_{1,8}=1, c_{1,11}=0\), 同时由布尔函数的性质可知还需添加一个条件:\(a_{1,7}=b_{0,7}\)
\(b_1'=(b_0+F(c_1[-8,11].d_1[7],a_1)+m_3)<<<19\)
\(b_1'=b_1[26]\)的条件是\(b_{1,26}=0\), 同时由布尔函数的性质可知还需要添加条件:\(d_{1,8}=a_{1,8}, d_{1,11}=a_{1,11}, c_{1,7}=1\)。这里需要注意的是,我们本来可以通过布尔函数的性质\(b_1'=b_1\)的,但实际却是使\(b_1'=b_1[26]\),这样做的原因主要是使其符合能够产生碰撞的路径。如果添加的限制条件只是让布尔函数里的差分无效的话,那么将很难处理算法最后一轮中在消息字上的差分,所以需要保留差分来抵消后面出现的差分。
这里再额外给出对\(c_2'=c_2[19,20,-21,22]\)的限制条件推导,可以从上面第一个表中的右边倒数第二列中看出,\(c_2'\)加上的差分实际是\(-2^{18}+2^{21}\),也就是说\(c_2'=c_2-2^{18}+2^{21}\),那么\(c_2'\)是如何等于\(c_2[19,20,-21,22]\)的呢?其实就是前面所说过的差分扩散。当\(c_2\)的第19位等于0时,加上\(-2^{18}\)会产生进位,而\(c_2\)的第20位也是0,那么会继续进位,直到第21位为1才停止。从差分的角度来理解,这样处理使得差分\(-2^{18}\)变成了\(2^{18}+2^{19}-2^{20}\),这样一来就同时改变了三个位:第19位:0->1,第20位:0->1,第21位:1->0,从而使其可以用扩散出去的差分来抵消掉后面出现的一些差分。
差分扩散与差分聚合:
差分扩散比如差分是\(2^{-18}\),如果第19位上是1,那么差分只会改变第19位;而如果第19位是0,那么差分会继续向高位扩散,知道遇到第一个1;
差分聚合则与之相反,如果差分使得第21个比特由1变成0,第22个比特由0变成1,那么其数学表达形式就是 \(-2^{20} + 2^{21} = 2^{20}\),也就是说最终将差分引起的变化聚合到了第21个比特上,但是变化的方向与原来的方向相反。
关于消息的修改的理解:
从前面的内容可以知道,如果一个消息在MD4算法中产生的链接变量符合一定的限制条件,我们就能通过在消息字中加上差分来构造出与原来的消息有着相同散列值的报文。
那么现在最关键的步骤就是找到构造这么一条满足限制条件的消息了。
对于消息的构造分为两个大的步骤:
先通过第一轮MD4算法中的限制条件来构造一条消息(16个消息字)。
然后再通过修改这些消息使其满足第二轮MD4算法中的限制条件。
首先是构造消息,其实这一步就是MD4算法的一个逆向过程。先给出一个随机变量,然后对其进行修改而是其满足所给的限制条件。然后利用MD4算法的逆向过程生成对应的消息字。这里给出由d1生成m1的代码实现过程:
unsigned int d1=rand();
d1=d1&(~(1<<6)); //这一步可以满足d1,7=0的限制条件
unsigned int d1_8=d1&(1<<7);
unsigned int a1_8=a1&(1<<7);
unsigned int d1_11=d1&(1<<10);
unsigned int a1_11=a1&(1<<10);
d1=d1^(d1_8^a1_8)^(d1_11^a1_11); //这一步可以满足d1,8=a1,8, d1,11=a1,11的限制条件
unsigned int m1=ROT_R(d1,7)-d0-F(a1,b0,c0); //MD4的逆向过程,生成m1
利用这样的方法可以构造16个满足第一轮限制条件的消息字。然后再继续修改这16个消息字,使其满足后面第二轮的限制条件。
这里有两种消息修改的方法分别以下面两个表的形式给出:
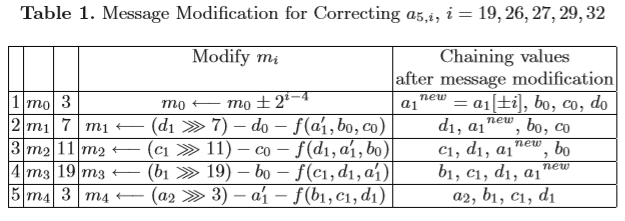
表1的意思其实不难懂,先看a5是如何生成的,a5=(a4+G(b4,c4,d4)+m0)<<<3,所以如果a5的第 i 位不满足条件,则可以通过对m0的第i-3位求反(这样就相当于对a5的第 i 位取反)来使其满足条件。(在原文中是使用 ± 操作,但实际可以通过异或2i-4来达到对m0的第i-3位取反的目的)
然后由于修改了m0,所以第一轮算法中由m0生成的a1也需要改变,而改变了a1,后面4个消息字的生成也就需要重新计算。这实际上可以看作是一种更新。

相对于表1,表2就比较难以理解了。但实际上,这两种方法的核心思想都是一样的,都是通过对相应的消息字的第 i-s 位 (s为相应的位移量) 进行取反来达到对链接变量的第 i 位取反的目的。
实现对m8的第i-9位取反的。需要注意的是,这里的计算不考虑其他位上的差分,并且这里的c5的限制条件都是第 i 位等于1。
\(d_2=(d_1+F(a_2,b_1,c_1)+m_5+2^{i-17})<<<7, d_2'=d_2+2^{i-17}\),在条件\(d_{2,i-9}=0\)的限制下,\(d_2'=d_2[i-9]\)
\(c_2=(c_1+F(d_2[i-9],a_2,b_1)+m_6)<<<11\),在条件\(a_{2,i-9}=b_{1,i-9}\)的限制下,\(c_2'=c_2\)。
\(b_2=(b_1+F(c_2,d_2[i-9],a_2)+m_7)<<<19\),在条件\(c_{2,i-9}=0\)的限制下,\(b_2'=b_2\)。
\(a_3=(a_2+F(b_2,c_2,d_2[i-9])+m_8-2^{i-10})<<<3\),在条件\(b_{2,i-9}=0\)的限制下,\(F(b_2,c_2,d_2[i-9])=F(b_2,c_2,d_2)+2^{i-10}\),于是在消息字m8上加一个 \(-2^{i-10}\) 的差分,这样就能达到对m8的第i-9位取反的目的同时还没有对链接变量a3造成修改。
\(d_3=(d_2[i-9]+F(a_3,b_2,c_2)+m_9-2^{i-10})<<<7\),不需要添加任何限制条件,\(d_3'=d_3\)。
其实总结下看的话,表1的修改方式就是直接对相应的消息字进行修改,而表2的方法则是通过在前面产生差分来达到修改报文的目的。
关于碰撞路径的推导:
如果给出一条碰撞路径,那么可以根据路径推导出需要的限制条件,并且可以通过相应的差分给出碰撞报文。
但问题是,如果求出一条碰撞路径呢?
我们已经知道,碰撞路径中需要通过在前面保留一些差分来抵消后面难以处理的差分,这需要很巧妙的设计。设计这样一条碰撞路径有什么可以依赖的规律,这对我来说仍然是个悬而未决的问题。。。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号