椭圆曲线的基本概念
椭圆曲线
设F是一个域，a,b\(\in\)F，则方程\(y^2=x^3+ax+b\)称为域F上的椭圆曲线。
上述方程称为维尔斯特拉斯方程，其判别式为\(y^2+axy+by=x^3+cx^2+dx+e\)
比如，实数域上的椭圆曲线如下：
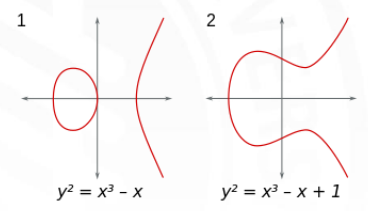
椭圆曲线上的加法：
设F是一个域，a,b\(\in\)F，令E={(x,y)|\(y^2=x^3+ax+b\)}\(\cup\){\(\infty\)}，其中{\(\infty\)}为无穷远点，则可以定义椭圆曲线上的加法为：
1)设\(P_1,P_2\in E\)，令R为\(P_1,P_2\)两点连线与椭圆曲线的交点关于X轴的对称点，则\(P_1+P_2=R\)
2)如果\(P_1,P_2\)两点关于X轴对称，那么规定他们连线与椭圆曲线相交于无穷远点，记为O
3)任何一个点通过上面的运算规则与O相加的和都是它本身
椭圆曲线上的加法的性质：\(\forall P,Q,R\in E\)，如果P,Q,R在一条直线上，那么P+Q+R=O
定理：若规定O+O=O，则(E,+)构成一个阿贝尔群（交换群），其中\(\infty\)为单位元，记为O，P=(x,y)的逆元为Q=(x,-y)
实例：设\(y^2=x^3+x+6\)是\(F_{11}\)上的椭圆曲线，求(3,6)+(5,2)
k=\(\frac{6-2}{3-5}=9\)
y-6=k(x-3)
y=9x+1
将上式代入\(y^2=x^3+x+6\)中得：
\((9x+1)^2=x^3+x+6=x^3+7x^2+5x+5\)
(x-3)(x-5)(x-7)=0
\(\therefore\) x=7
y=9x+1=9
\(\therefore\)(3,6)+(5,2)=(7,-9)=(7,2)
椭圆曲线密码
以下三类公钥系统被认为是安全有效的:
- 基于大整数分解问题的RSA型公钥密码；
- 基于有限域上离散对数问题的ElGamal型公钥密码；
- 基于椭圆曲线离散对数问题的椭圆曲线公钥密码。
椭圆曲线公钥密码优势：对于椭圆曲线离散对数问题，目前不存在亚指数时间算法，从而为达到相同安全性所需的密钥尺寸更小:
– RSA 密码体制：模长1024 比特；
– 椭圆曲线密码体制：模长160 比特。
椭圆曲线密码体制适用于计算、存储、带宽受限，但又要求高速实现的应用领域，例如智能卡、无线通讯等。
El'Gamal密码方案的椭圆曲线形式：
- Gen：设E为\(F_q\)上的椭圆曲线，一般记为E(\(F_q\))，设P = \((x_p,y_p)\in E(F_q)\)，且P的次数足够大，任取1 < s < ord(P)，令Q = sP = (\(x_q,y_q\))，则E(\(F_q\))，P，Q为公钥，s为私钥
- Enc：消息m满足0 \(\le\) m < \(F_q\)，任取1 < r < \(F_q\)，计算(\(x_1,y_1\)) = rP，(\(x_2,y_2\)) = rQ，c = m·\(x_2\)，则密文为(\(x_1,y_1,c\))
- Dec：计算(x',y') = s(\(x_1,y_1\))，再计算m'=c·\(x'^{-1}\)
正确性验证：(x',y') = s(\(x_1,y_1\)) = srP = rsP = rQ = (\(x_2,y_2\))，所以x' = \(x_2\)，m' = c·\(x'^{-1}\) = c·\(x_2^{-1}\) = m·\(x_2·x_2^{-1}\) = m
