密码学基础(六) - 密钥分发与管理

私钥加密体系的实际应用中存在三个问题：

1. 密钥的分发
2. 存储和管理大量的密钥
3. 私钥加密体系在开放系统中的不适用性

密钥分发中心(Key-Distribution Center, KDC)

KDC的运行机制：

1. 首先，Alice和KDC共享一个密钥k_A，Bob和KDC共享一个密钥k_B
2. Alice向KDC发送一条信息：“I, Alice, want to talk to Bob”
3. KDC接收到消息后选择一个会话密钥k，然后用kA将k进行加密后发送给Alice，同样的，用密钥k_B将k加密后发送给Bob
4. 只要Alice和Bob恢复了会话密钥，他们就可以进行私密的会话了
5. 会话结束后，需要擦拭掉会话密钥

KDC的图示：

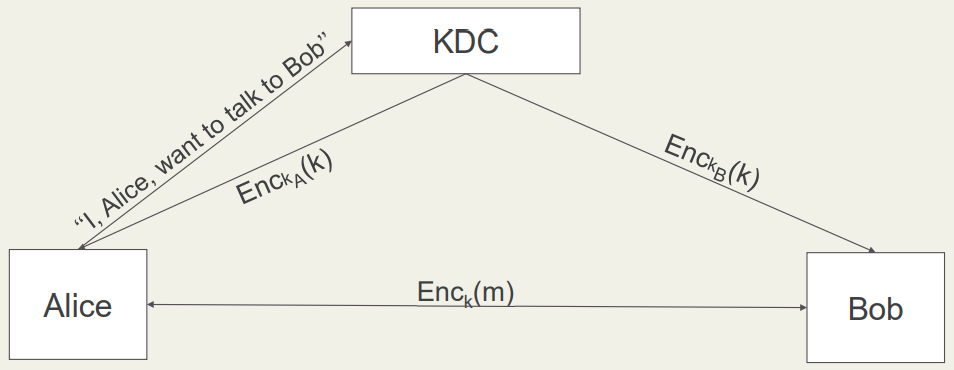
KDC的优点：

• 每个用户只需要与KDC维持一个长期的密钥，而且用户需要管理并存储会话密钥，但这个会话密钥时短期的
• KDC需要保存很多密钥，然而，KDC可以放在安全的地方，并且有抵抗网络攻击的安全手段
• 每当一个用户加入时，只需要添加一个该用户与KDC之间的密钥

KDC的缺点：

• 如果成功攻击了KDC，那么着整个系统都会被破解
• KDC是单点故障:如果KDC停机，则暂时无法进行安全通信

KDC的密钥分发协议

这个协议其实就是在原来KDC的运行机制的基础上做了一点改进：

当Alice向KDC发起与Bob会话的请求后，KDC用k_A将会话密钥加密发送给Alice，然后又用k_B将会话密钥发送给Alice，然后Alice在向Bob发起会话，并同时将Enc_kB(k)发送给Bob。

图示如下：

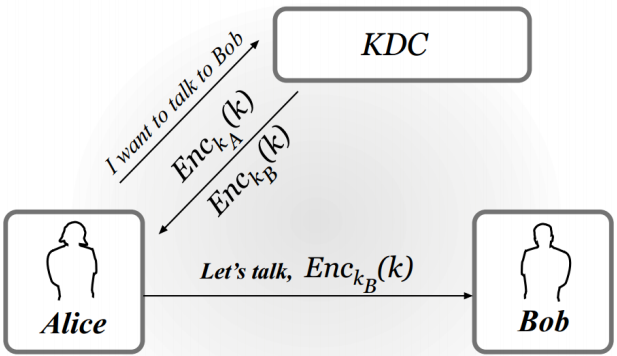
KDC的密钥分发协议的优点：

• 该协议减少了KDC上的通信负担。
• KDC不需要启动到Bob的第二个连接，也不需要担心Alice启动协议时Bob是否在线。 
• 此外，如果Alice保留了票据(以及会话密钥副本)，那么就可以通过简单地将票据重新发送给Bob来重新启动与Bob的安全通信，而需要再次向KDC发起请求。

然而密钥分发协议并没有降低KDC的安全隐患问题

密钥交换与迪菲-赫尔曼(Diffie-Hellman)协议

KDC体系中还存在一个问题就是需要用一条私密的信道来分享用户与KDC之间的密钥

Diffie和Hellman意识到不对称现象可以被用于推导安全密钥交换的交互协议，允许双方通过一条公共信道来分享一个密钥，并且允许双方执行他们可以逆转但窃听者不能逆转的操作。

密钥交换协议的安全性：协议执行过程中，窃听者无法区分由协议生成的密钥和一个随机的二进制串

密钥交换协议的安全实验：KE^eav_A,Π(n):

1. 通信双方在执行协议的时候需要维护一个安全参数1ⁿ，这将生成一个包含各方发送的所有消息的文本trans，以及各方输出的密钥k。
2. 随机的选择一个比特b，如果b = 0，则令k^ = k；如果b = 1，则随机的选择k^∈{0, 1}ⁿ
3. 将trans和k^发送给敌手，然后敌手输出一个比特b‘
4. 如果b' = b，则这个实验输出1；否则输出0

定义：如果存在一个可忽略函数negl对所有运行在PPT上的敌手都有Pr[KEeavA, Π(n)=1] ≤ 1/2 + negl(n)，则称这个密钥交换协议是安全的。

Diffie-Hellman协议

Diffie-Hellman协议的构造方法：

首先通信双方都需要输入一个安全参数1ⁿ，然后运行协议：

1. Alice运行 ç(1ⁿ) 从而获得(G, q, g)
2. Alice随机的在Z_q中选择一个x，然后计算h_A := g^x
3. Alice发送(G, q, g, h_A)给Bob
4. Bob收到(G, q, g, h_A)后，随机的在Z_q中选择一个y，然后计算h_B := g^y，并将h_B发送给Alice，然后输出密钥k_B := h_A^y
5. Alice收到hB后输出密钥k_A := h_B^x

Diffie-Hellman协议的图示：

离散对数问题的难度对于协议的安全性来说是必要的，但不是充分的，因为有可能存在其他方法来计算密钥k_A=k_B，而不需要显式地计算x或y。

密钥交换协议所要求的是共享密钥g^xy对于给定g、g^x和g^y的任何敌手都应该与某个随机的数不可区分，而这正是DDH(Decision Diffie-Hellman)假设。

DDH问题，假设存在一个可忽略函数对所有PPT上的敌手 A 都有：
|Pr[A(G, q, g, g^x, g^y, g^z)=1] - Pr[A(G, q, g, g^x, g^y, g^xy)=1]| ≤ negl(n)

定理：如果DDH问题在群G中是难以解决的，那么Diffie-Hellman密钥交换协议在被动攻击下是安全的。

证明.

在开始证明之前需要将前面的KE^eav_A,Π实验进行一定的修改：当b=1时，随机的选择一个群G中的元素，而不是一个n比特长的随机二进制串，则：

Pr[KE^eav_A,Π(n)=1]

=1/2(Pr[KE^eav_A,Π(n)=1 | b=0] + Pr[KE^eav_A,Π(n)=1 | b=1])

=1/2(Pr[A(G, q, g, g^x, g^y, g^xy)=0] + Pr[A(G, q, g, g^x, g^y, g^z)=1])

=1/2(1-Pr[A(G, q, g, g^x, g^y, g^xy)=1] + Pr[A(G, q, g, g^x, g^y, g^z)=1])

=1/2(1-(Pr[A(G, q, g, g^x, g^y, g^xy)=1]  - Pr[A(G, q, g, g^x, g^y, g^z)=1]))

=1/2(1 - negl(n))

=1/2 - 1/2negl(n)

所以Diffie-Hellman密钥交换协议是安全的。

然而在实际应用中，Diffie-Hellman协议对于中间人攻击是完全不安全的。