密码学基础(二) - 完美保密

完美保密

一个在明文空间M上的加密方案（Gen，Enc，Dec），如果对于每个明文 m ∈ M，对每个密文c ∈ C，其中Pr[C=c]>0，有：

Pr[ M = m | C = c ] = Pr[ M = m ]

则称这种加密方案是完美保密，换句话说，即在“已知了密文的情况下，得到明文的概率”和“在不知道密文的情况下，得到明文的概率”是相等的。

引理：一个在明文空间M上的加密方案是完美保密的，当且仅当，对于每个明文m，m‘ ∈ M，以及每个密文 c ∈ C有：

Pr[ EncK (m) = c ] = Pr[ EncK (m′) = c ]

即加密不同的明文得到相同的密文的概率是一样的（这个概率是通过遍历密钥空间得出来的）。

引理的证明：

充分性：

如果Pr[M=m] = 0，那么Pr[M=m | C=c] = 0 = Pr[M=m]

如果Pr[M=0] > 0，则：

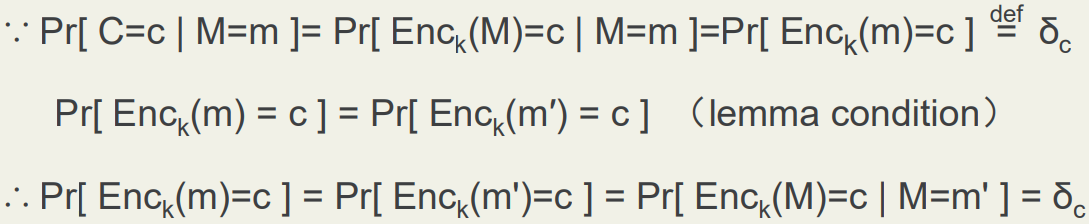
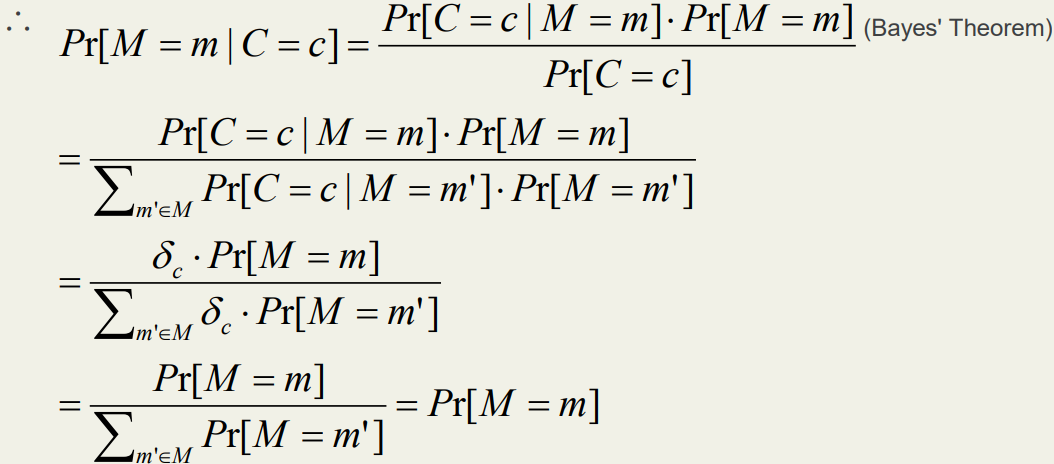
 必要性：

∵Pr[M=m | C=c] = Pr[C=c | M=m] * Pr[M=m] / Pr[C = c]

 且Pr[M=m | C=c] = Pr[M=m]

∴Pr[C=c | M=m] * Pr[M=m] / Pr[C=c] = Pr[M=m]

Pr[C=c | M=m] / Pr[C=c] = 1

Pr[C=c | M=m] = Pr[C=c]

Pr[C=c and M=m] / Pr[M=m] = Pr[C=c]

∴事件“M=m”与事件“C=c”是两个相互独立的事件

则任意m, m‘ ∈ M，有

Pr[C=c | M=m] = Pr[C=c | M=m']

Pr[Enc_k(m)=c] = Pr[Enc_k(m')=c]

完美不可区分

 关于完美不可区分性的定义是基于一个涉及对手A的实验，并形式化了A无法区分一种明文加密和另一种明文加密;因此我们称之为对抗性的不可分辨性。

窃听实验（PrivK^eav_{A, Π}）：

1. 敌手A输出一对明文m0，m1 ∈ M
2. 运行Gen生成一个随机密钥k，并选择一个统一的bit b∈{0,1}。计算密文c←Enck(mb)，并返回给A。
3. A输出一个比特b’
4. 这个实验的输出为 1 ，当 b=b‘ 的时候；否则输出 0 。记PrivK^eav_{A, Π} =1，如果实验输出 1，并且在这种情况下，称A成功猜中了密文对应的明文。

完美不可区分的定义：一个在明文空间M上的加密方案：Π = (Gen, Enc, Dec)是完美不可区分性的，当且仅当对每个敌手A都有：

Pr[PrivK^eav_{A, Π} =1] = 1/2

引理：一个加密方案 Π 是完美保密的，当且仅当它是完美不可区分的。

引理的证明：

充分性：基于窃听实验可以将完美不可区分性表示为：

Pr[M=m₀ | C=c] = Pr[M=m₁ | C=c] = 1/2

∵ M = {m₀,m₁}  即，明文空间中只有m₀和m₁

∴Pr[M=m] = 1/2

∴Pr[M=m | C=c] = Pr[M=m]

满足完美保密的定义，所以充分性满足

必要性

根据完美保密引理可知：如果满足完美保密，则有

Pr[Enck(m₀)] = Pr[Enck(m₁)]

Pr[C=c | M=m0] = Pr[C=c | M=m1]

Pr[M=m₀ | C=c] Pr[C=c] / Pr[M=m₀] = Pr[M=m₁ | C=c]Pr[C=c] / Pr[M=m₁]

Pr[M=m₀ | C=c] / Pr[M=m₀] = Pr[M=m₁ | C=c] / Pr[M=m₁]

∵Pr[M=m₀] = Pr[M=m₁]

∴Pr[M=m₀ | C=c] = Pr[M=m₁ | C=c] 

而这又恰好是完美保密的另一种表示形式

所以必要性满足

实例：证明维基尼尔加密不是完美不可区分的，至少对于某些确定的参数

设 Π 为两个长度为 2 的字符串的明文空间上的维基尼尔加密方案，并且密钥周期概率均匀地在{1，2}中选择。

敌手 A 的实验策略：

输出两条明文m₀ = aa，m₁ = ab

对于返回的密文c = c₁c₂，敌手的输出策略为：如果c₁ = c₂，则输出 0 （即认为被加密的明文是m₀）；否则输出 1

敌手 A 实验成功的概率：

Pr[PrivK^eav_{A, Π} =1] = ( Pr[A outputs 0 | M=m₀] + Pr[A outputs 1 | M=m₁] ) / 2

所以可以分两种情况进行讨论：

• M=m₀时

如果密钥的周期为1，那么敌手输出 0 的概率为1

如果密钥的周期为2，那么只有当密钥的第一个字母和第二个字母恰好相等的情况下敌手才能输出 0 ，即在这种情况下敌手输出 0 的概率为1/26

∴ Pr[A outputs 0 | M=m₀] = ( 1/2 + 1/2 * 1/26 ) = 27/52

• M=m₁时

Pr[A outputs 1 | M=m₁] = 1 - Pr[A outputs 0 | M=m₁]

如果被加密的明文为m₁，那么只有当密钥的周期为2，并且密钥的第二个字母恰好比第一个字母小 1 的时候，敌手才会输出 0 。

∴Pr[A outputs 0 | M=m₁] = 1/2 * 1/26

∴Pr[A outputs 1 | M=m₁] = 1 - Pr[A outputs 0 | M=m₁] = 51/52

综上：Pr[PrivK^eav_{A, Π} =1] = ( Pr[A outputs 0 | M=m₀] + Pr[A outputs 1 | M=m₁] ) / 2 = 3/4 > 1/2

所以在此参数下的维基尼尔加密方案并不是完美保密的

One-Time Pad

One-Time Pad加密方案的构造：

选择一个确定的整数 l > 0，那么加密方案的明文空间，密文空间，以及密钥都是长度为 l 的01串

• 密钥生成算法Gen：生成一个长度为 l 的01串
• 加密算法Enc：输入一个长度为 l 的01串密钥 k ，以及一个长度为 l 的01串明文 m，输出密文 c = k ⊕ m
• 解密算法Dec：输入一个长度为 l 的01串密钥 k ，以及一个长度为 l 的01串密文 c ，输出明文 m =k ⊕ c

加密方案的正确性验证：Deck( Enck(m) ) = k ⊕k ⊕m = m，所以这是一个正确的加密方案

证明One-Time Pad加密方案是完美保密的：

首先计算：Pr[C=c | M=m]，对任意的c∈C以及任意的m∈M有：

对任意的c ∈ C

 

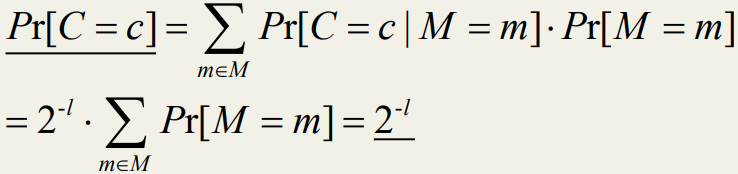
由贝叶斯定理得：

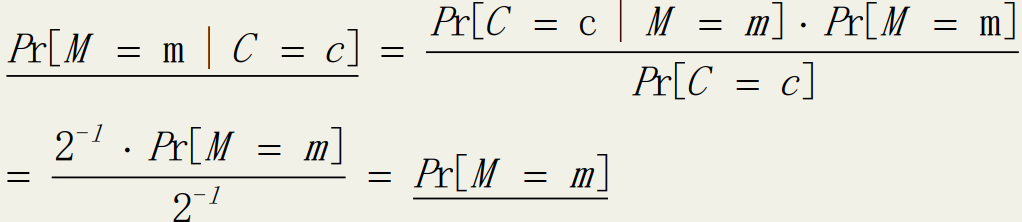
 ∴此加密方案是完美保密的

完美保密的局限性

• 完美保密的加密方案的密钥长度至少要和明文的长度一样大

定理：如果一个在明文空间 M 且密钥空间K的加密方案Π(Gen, Enc, Dec)是完美保密的，则|K| ≥ |M|

证明：反证法，假设 |K| < |M| 

设集合M(c) = {m | m = Deck(c)，for some k ∈ K}

∵|K| < |M|

∴存在一些m‘ ∈ M，m’ ∉ M(c)

则Pr[M=m' | C=c] = 0 ≠ Pr[M=m]

所以根据完美保密的定义可知，在此种加密方案并不是完美保密

• 密钥只能被使用一次

假设有两个明文使用了相同的密钥进行加密

如果一个敌手通识获取了c = m ⊕ k 以及c′ = m′ ⊕ k ，那么可以计算：c ⊕ c′ = (m ⊕ k) ⊕ (m′ ⊕ k) = m ⊕ m′ 

敌手因而可以获取两个明文m和m‘的异或取值，而完美保密要求敌手无法通过密文获取任何关于明文的信息

香农定理（用于判断是否是完美保密）

假设对明文空间M上的加密方案Π(Gen, Enc, Dec)有|M| = |K| = |C|，则这种加密方案是完美保密当且仅当：

1. 对任意密钥k ∈ K，k 被选中的概率都相等，都等于 1/|K|
2. 对于任意的明文m ∈ M，以及任意的密文c ∈ C，则存在一个唯一的密钥 k ∈ K使得Enc_k(m) = c