密码学基础(一) - 导论基础

加密算法的语法

密钥空间K：密钥生成算法能够生成的所有密钥的集合

明文空间M：所有合法明文的集合

密文空间C：所有可能的密文的集合，这个集合同时由密钥空间K和明文空间M定义

一个加密方案通常由三个算法：(Gen、Enc、Dec)以及明文空间明确定义

Gen：密钥生成函数，以安全参数作为输入，然后将密钥作为输出的算法

Enc：加密算法，以密钥以及明文作为输入，然后输出一段密文

Dec：解密算法，将密钥以及密文作为输入，然后输出对应的明文

一个加密方案必须满足的要求是：对于任意 k 属于K ，以及任意明文 m 属于M有，Dec_k(Enc_k(m)) = m

Kerckhoff's的三条主要结论

1. 对于通信用户来说，维护一个比短小的密钥，比维护一个算法的隐蔽性要简单的多
2. 对于诚实的通信者来说，更换密钥比更换加密算法要简单的多
3. 对于所有用户来说，使用相同的加密算法用不同的密钥进行加密，会比所有人使用不同的加密算法要简单的多

古典密码以及密码分析

移位密码

移位密码类似凯撒密码，但是凯撒密码的密钥是固定为3的，而移位密码的密钥是进行引入了的，如下：

 密钥用一个字母表示，比如“a”=0，“b”=1，…

 显然，这样的加密方案很容易进行暴力破解。

充分的密钥空间原则：任何安全加密方案都必须有一个密钥空间，该空间不容易受到彻底搜索的攻击。而在如今这个时代，密钥空间的大小应该在2⁶⁰到2⁷⁰之间。但这对于加密方案来说只是一个必要条件而非充分条件。

字母替换密码

字母替换密码的加密思想是：将明文字符随机的映射到不同的密文字符上，但这种映射关系必须是一对一的，以便解密。下面给出一个例子：

 所以对明文tellhimaboutme可以加密成GDOOKVCXEFLGCD

这种密码算法的密钥空间为26!=26*25*...*1 ≈ 2⁸⁸

在这种情况下，暴力破解是不可行的，因为密钥空间很大，不能够进行彻底搜索。

然而这并不意味着这种密码算法就一定是安全的

除了暴力破解，还可以是统计分析攻击

使用英文字母中每个字母在现实中使用的频率可以大致推断出相应的映射关系

对于长的密文，密文出现频率最高的字母对应于使用频率最高的字母e，然后依次以此类推。

对于短的密文，需要使用显示经验，比如在字母“t”和“e"之间通常是字母"h"，单词“the”；字母”u“通常跟在字母”q”后面，前缀“qu-”。

利用字母频率表来实现移位密码的自动化破解

虽然能使用暴力破解的方式来破解一个移位密码的密文，但是机器并不能自动识别到底哪一条才是我们所欲需要的明文。

而现在，可以使用字母频率表来优化移位密码的破解方法，能够使机器自动识别目标明文。

设p_i，0≤ i ≤25，为普通的现实中每个字母出现的频率，那么根据上面的字母频率表可以计算得出：

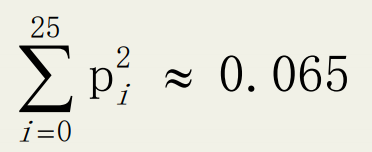
设q_i，0≤ i ≤25，为目标密文中字母表第 i 个字母出现的频率。那么如果密钥为k那么q_i+k应该约等于pi，对于0≤ i ≤25。

对于每个可能的密钥，设密钥的值为j，j∈{0, ..., 25}，计算：

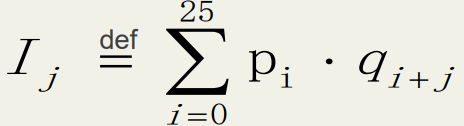
 当I_j≈0.065的时候，则 j 为所需要的密钥k。

可以通过上述方法实现移位密码的自动破译，下面给出相关的Python代码

p = [8.2,1.5,2.8,4.3,12.7,2.2,2.0,6.1,7.0,0.2,0.8,4.0,2.4,
     6.7,1.5,1.9,0.1,6.0,6.3,9.1,2.8,1.0,2,4,0.2,2.0,0.1]
for i in range(0,26):
    p[i] = p[i]/100
sum = 0
for i in p:
    s = i ** 2
    sum = sum + s
c = "OVDTHUFWVZZPISLRLFZHYLAOLYL"   #密文
q = []
for ch in range(ord("A"),ord("Z")+1):
    cnt = c.count(chr(ch))
    pro = cnt / len(c)
    pro = pro
    q.append(pro)
result = []
copy = []
for i in range(0,26):
    mult = 0
    for j in range(0,26):
        index = (j + i)%26
        mult = mult + (q[index] * p[j])
    temp = abs(mult - sum)
    result.append(temp)
    copy.append(temp)
copy.sort()
minal = copy[0]
k = result.index(minal)
print("key is",k)
for ch in c:
    shift = ((ord(ch) - ord("A") - k)%26)+ord("a")
    print(chr(shift),end="")

 输出的结果为：

========= RESTART: D:\Python\Code\Improved_attack_on_shift_cipher.py =========
key is 7
howmanypossiblekeysarethere

维基尼尔密码（多表字母替换密码）

在维基尼尔密码中，一个长度较短的单词被作为密钥，而加密的过程就是通过对每个明文中的字母依次“加上”密钥的字母。下面是一个例子：

 显然，在这种加密方案下，前面所提到的暴力破解和统计分析攻击都无法起到作用。这种密码虽然是在16世纪发明的，但是对于这种密码的一种系统性的攻击方案过了数百年后才被设计出来。

如果能够知道密钥的长度，那么对于密文的破解工作将会非常的简单。

假设密钥的长度（密钥长度有时候也被称作密钥周期）为 t ，那么可以将密文分成几个部分，其中的每个部分都可以看作是使用移位密码加密的实例。

设密钥为k = k₁, k₂, ..., k_t，（ki是密钥的一个字母）

密文为c = c₁, c₂, ..., 为密文的每个字符

然后对于 j (1≤j≤t）那么对于字母c_j, c_j+t, c_j+2t, ...，它们是由密钥为k_j的移位密码加密的。

也就是说将密文中的字符每 t 个字符分为一组，然后每组字符中位置相对应的字母是使用了同一个密钥进行移位加密的密文。

在这种情况下，并不能使用暴力破解来解密分好组的字符，因为它们在明文中也是不连续的。所以只能使用统计分析攻击的方法来破解处理过后的密文。

如果不知道密钥的长度，那么最有效的方法是Kasiski方法：

1.  首先，识别密文中长度为2或3的重复模式。
2. 因为英语中经常出现的一些二叉或三叉结构。 
3. 考虑英语文本中经常出现的单词“the”。
4. 显然，“the”将根据其在文本中的位置映射到不同的密文字符。
5. 但是在长文本中，“the”很有可能被重复映射到相同的密文字符

现代密码学的基本原则

原则1：正式化的定义

1. 设计：能够使人理解加密方案。
2. 研究：有了正式的定义，就可以研究加密方案的是否达到了所需要的安全性。
3. 评估：通过精确的定义，可以中两个方案之间进行评估和权衡。
4. 使用：加密方案的定义能够加密方案使用的安全性。决定在较大的系统中使用哪种加密方案；理解需要什么安全概念，然后找到满足该概念的方案；较弱的安全概念也许能够达到要求。

加密方案的安全性：

• 不能泄露密钥给攻击者；
• 不能允许攻击者通过密文恢复整个明文；
• 不能允许攻击者通过密文恢复明文中的任何一个字符；
• 不论攻击者有着何种的能力背景，不能从密文中泄露任何明文中的潜在信息。

威胁模型：

• 唯密文攻击：这是一种最基本的攻击类型，指敌手通过观察一个或多个密文，然后试图通过密文中潜在的规律来获取明文。
• 已知明文攻击：指敌手获取了一对或多对使用某种密钥加密的明文/密文对。然后通过密文推断使用相同密钥加密的明文。
• 选择明文攻击：敌手能够选择明文进行加密。可以进行已知明文攻击。
• 选择密文攻击：敌手能够选择密文进行解密，然后同样的，可以分析出密文中潜在的明文信息。

原则2：精确的假设

 精确假设的第一个原因：假设的检验

• 假设是未被证明但却被推测为正确的陈述。
• 为了加强我们对某些假设的信念，有必要对假设进行研究。
• 如果所依赖的假设没有得到准确的陈述和呈现，就无法对其进行研究和(潜在的)反驳。

精确假设的第二个原因：加密方案的比较，提出了两种方案，它们都可以被证明满足某种定义，但每个方案都有不同的假设，假设两种方案的效率相同，那么应该选择哪种方案?

• 基于较弱假设的方案是首选。
• 如果两种方案所使用的假设是不可比较的，那么一般的规则是选择基于更好研究的假设的方案，或者基于更简单的假设。

精确假设的第三个原因：理解必要的假设，如果在后续构建块中发现一些弱点，为了判断加密方案是否仍然安全，则：

如果有关构建块的基本假设作为证明方案安全性的一部分被阐明，那么我们只需检查所需的假设是否受到新发现的弱点的影响。

原则3：安全性证明

密码学结构应伴随严格的安全证明，根据原则1制定的定义，并相对于假设(如果有)，这与原则 2 一样。

安全性的证明提供了坚固的保证(相对于定义和假设)，即任何具有特定资源的对手都不能破解这个加密方案。

经验表明，在密码学和计算机安全方面的直觉是灾难性的。