Lambda代数

lambda abstraction（lambda abstraction）

在lambda运算中，函数的表达式与平常的不同：

f(x)=M，应该表示成λx.M（带函数名的写法为，f≡λx.M）的形式，这样左到目的是为了省略函数的名称，从而更加简洁

lambda abstraction中点号的后面包括到最右边的部分，例如，λx.MN等同于λx.(MN)，而不是(λx.M)N

多维的lambda abstraction的表达式可以缩写，例如，λxyz.M等同于λx.λy.λz.M

自由变量和受限变量

变量x在lambda abstraction中λx.N中被称作是受限变量，其中λx被称作binder，而N被称为binder的受限范围。

不是受限变量的变量就是自由变量

在表达式M中出现的自由变量记作FV(M)，并且有下面几条性质：

• FV(x) = {x}
• FV(MN) = FV(M)∪FV(N)
• FV(λx.M) = FV(M)\{x}

重命名

将表达式M中的变量x重命名为y的时候写作M{y/x}

重命名有以下几条运算性质

x{y/x} ≡ y

z{y/x} ≡ z, if x ≠ z

(MN){y/x} ≡ (M{y/x})(N{y/x})

(λx.M){y/x} ≡ λy.(M{y/x})

(λz.M){y/x} ≡ λz.(M{y/x}), if x ≠ z

α等式

α等式是一种逻辑推理方式，书写的形式类似于分式，横线的上方是推理的条件（如果横线的上方没有语句，则意味着不需要任何条件，横线下方的表达式成立），下方是推理的结论，如下：

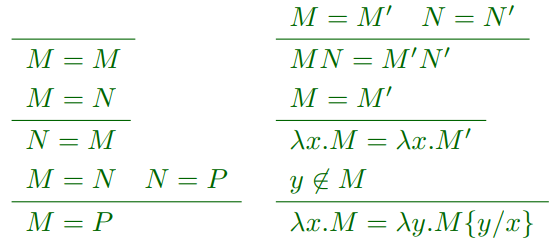
 替换

用表达式N替换表达式M中出现的自由变量x，符号写作：M[N/x]，其运算规律如下：

x[N/x] ≡ N

y[N/x] ≡ y, if x 6= y

(MP)[N/x] ≡ (M[N/x])(P[N/x])

(λx.M)[N/x] ≡ λx.M

(λy.M)[N/x] ≡ λy.(M[N/x]), if x ≠ y  and  y不属于F V (N)

(λy.M)[N/x] ≡ λy ’ .(M{y ‘ /y}[N/x]), if x ≠ y,  y不属于F V (N), and y ‘ fresh

 β-缩写

形如(λx. M)N的表达式被称为β所以缩写，等同于M[N/x]，下面是一个例子：

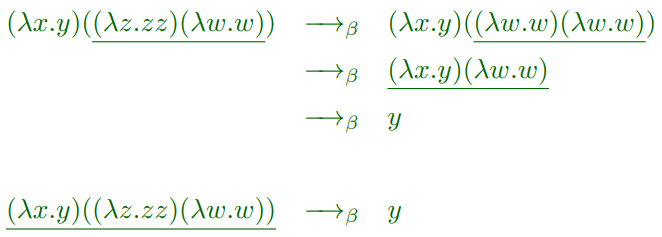
 β缩写具有下面几条运算性质：

1. 
2.  
3. 
4.  

递归函数与定点

定理：在lambda无类型运算中，每个函数都有一个定点。

证明：设Θ = AA，其中A = λxy.y(xxy)，则

ΘF = AAF

      = (λxy.y(xxy))AF

     →β F(AAF)

      = F(ΘF)

因此ΘF是F的一个定点，而Θ被称为图灵定点组合子（Turing’s fixed point combinator）

下面给出一个阶乘函数的定点：

fact n = if-then-else (iszero n)(¯1)(mult n(fact (pred n)))，递归调用求n的阶乘

fact = λn.if-then-else (iszero n)(¯1)(mult n(fact (pred n)))，再将函数转换成lambda abstraction的形式

fact = (λf.λn.if-then-else (iszero n)(¯1)(mult n(f(pred n))))fact，使用β-缩写的方法将用 f 来代替函数fact，从而将函数名fact移到外面，从而构成定点：

fact = Θ(λf.λn.if-then-else (iszero n)(¯1)(mult n(f(pred n)))

定义布尔类型

设T = λxy.x，F = λxy.y

则可以定义逻辑与运算为：and = λab.abF

and TT = (λab.abF)TT = TTF = (λxy.x)TF = T

and TF = (λab.abF)TF = TFF = (λxy.x)FF = F

and FT = (λab.abF)FT = FTF = (λxy.y)TF = F

and FF = (λab.abF)FF = FFF = (λxy.y)FF = F

相似的，可以定义逻辑或、逻辑非、异或运算以及if-then-else运算为

not = λa.aFT

or = λab.aTb

xor = λab.a(bFT)b

if-then-else = λx.x ( if-then-else TMN →β M；if-then-else FMN →β N)

定义自然数

设整数n的值表示为：n¯ = λfx.f ⁿ x，其中f ⁿx 为f(f(. . .(fx). . .))中 f 出现了n次的缩写

0 = λfx.x

1 = λfx.fx

2 = λfx.f(fx)

...

则successor函数可以定义为：succ = λnfx.f(nfx)

succ n = (λnfx.f(nfx))(λfx.f ⁿ x)

　　 →_β λfx.f((λfx.f ⁿ x)fx)　　(有三个固定变量，但是只有一个用于替换的表达式，所以后面两个固定变量没有被替换)

　　→_β λfx.f(f ⁿ x)

　　　= λfx.f ⁿ⁺¹ x

　　　= n+1

定义加法运算为：add = λnmfx.nf(mfx)

add mn = (λnmfx.nf(mfx))mn = (λfx.(λfx.f ⁿ x)f(λfx.f ^m x)fx) = (λfx.(λfx.f ⁿ x)f(f ^m x)) = (λfx.(λfx.f ⁿ x)f ^m+1 x) = λfx.f ^m+n x = m+n

定义乘法运算为：mult = λnmf.n(mf)

 mult mn= λnmf.n(mf)mn = λf.(λfx.f ⁿ x(λfx.f ^m x)f) = λf.(λfx.f ⁿ x(λx.f ^m x)) = λf.λx f ^m*n x = λfx.f ^m*n x = m*n

定义一个序对和元组(pairs，tuples)

一个序对<M,N>为：<M, N> = λz.zMN

设π1 = λp.p(λxy.x)；π2 = λp.p(λxy.y)

则显然能够得到：

π1<M, N> →β M

π2<M, N> →β N

 同样的，可以定义一个元组：<M₁, ..., M_n> = λz.zM₁...M_n

则第 i 个元素的投影可以定义为：π ⁿ _i = λp.p(λx₁...x_n.x_i )

显然：π ⁿ _i <M₁, ..., M_n> →β M_i      for all 1 ≤ i ≤ n

定义一个链表

 设 nil = λxy.y ；H :: T = λxy.xHT. 

则用于计算链表中所有元素的和的函数addlist可以写为

addlist l = l(λht.add h(addlist t))(0)

定义一个树

二叉树可以是由自然数标记的叶子，也可以是两个子树的节点，可以定义leaf(n)，为由自然数n标记的叶子；node(L, R)为具有左子树L和右子树R的节点：

leaf(n) = λxy.xn

node(L, R) = λxy.yLR

那么用于计算一个树中所有节点的和的函数可以写为：

addtree t = t(λn.n)(λlr.add (addtree l)(addtree r))

简单类型和粗糙类型

设集合 i 是基本类型的集合，那么在集合 i 上的简单类型的集合就是：

A, B ::= i | A→B | A×B | 1

其中：

• A → B is the type of functions from A to B
• A × B is the type of pairs <x, y>
• 1 is a one-element type, considered as “void” or “unit” type in many languages: the result type of a function with no real result

需要注意的是，×运算的优先级是高于→的，而→运算是右结合的。

而粗糙类型的定义为：

M, N ::= x | MN | λxA.M | hM, Ni | π1M | π2M | ∗