上下文无关语言的性质
上下文无关文法的范式
可以证明任何CFL都可以用只有A→BC或者A→α形式产生式的CFG产生，其中A，B和C是变元，而α是终结符。这种形式称为乔姆斯基范式(Chomsky Normal Form, CNF)。
为了得到这种形式的CFG，我们需要做很多初步的简化，而这些简化方法本身在很多方面都很有用：
- 我们必须去除无用符号。所谓无用符号，是指不出现在任何由开始符号推导出一个终结符串的过程中出现的变元和终结符号。
- 我们必须去除ε产生式。所谓ε产生式，是指A→ε形式的产生式，其中A是变元。
- 我们必须去除单位产生式，所谓单位产生式，是指A→B形式的产生式，其中A和B式是变元。
去除无用的符号：
显然，去除一个文法的无用符号并不会改变这个文法产生的语言，因此需要尽量检测和去除所有无用的符号。
我们去除无用符号的方法是通过识别一个有用符号一定能做到的两件事：
显然一个有用符号一定是产生的和可达到。如果我们首先去除不是产生的符号，再从剩余文法中去除不是可达的符号，剩下的符号一定只有有用的符号了。
下面给出一个例子：
考虑这样一个文法，它有如下的产生式：
S→AB | a
A→b
除了B以外，所有符号都是产生的：a和b产生它们自己，S产生a，A产生b。
如果去除符号B，我们一定要去除产生式S→AB，剩下的文法是：
S→a
A→b
可以发现现在，S和a是可达的。去除A和b后剩下的产生式只有S→a。只有该产生式的文法的语言是{a}，而这和原来的文法的语言相同。
获取所有产生的符号的集合：
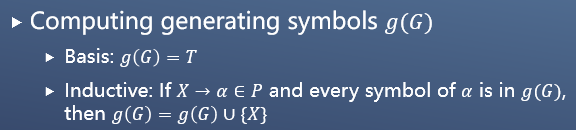
下面给出一个例子：
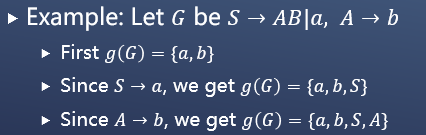
获取所有可达的符号的集合：
下面给出一个例子：
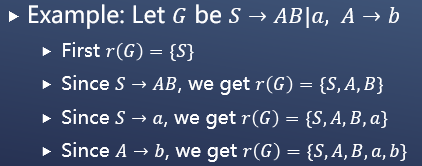
去除ε产生式：
如果一个语言L有一个CFG，则L-{ε}一定有一个不含ε产生式的CFG。如果ε不属于L，则L本身就是L-{ε}，因此L就有一个不含ε的产生式的CFG。
当一个变元满足下列条件时称其为可空的：
获取所有可空符号的集合：
去除ε产生式：
对于产生式A→w，应该考虑w中可空符号相互独立地存在或者不存在的组合，并将这些组合替换成新的产生式右边的结果。
下面给出一个例子：
**去除ε产生式：对于S→AB，相互独立地考虑AB存在或不存在的几种情况：AB，A，B，ε，所以S→AB应该替换成S→AB，S→A，S→B，S→ε。但是S→ε是不允许存在的，所以最终结果有三个。
去除单位产生式:
单位产生式在去除歧义性上是有用的，但是单位产生式会使某些证明变得复杂，而且它们也会给推导过程引入本来在技术上不需要的步骤。
如果一个变元对（A, B）满足下面的条件，则称其为单位对：
获取所有单位对的集合：
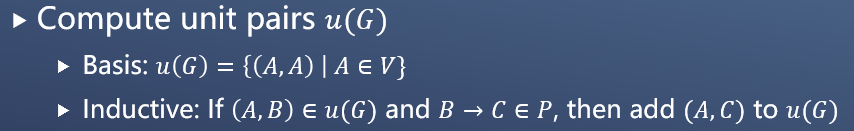
下面给出一个例子：
考虑某个文法的产生式：I → a | b | Ia | Ib | I1 | I0, F → I | (E), T → F | T×F, E → T | E+T，求出其所有的单位对：
由基础部分可以得到这些单位对：(E, E), (T, T), (I, I), (F, F)。对于归纳部分可以得出下面的结论：
(E, E)和产生式E→T可以得到单位对(E, T)
(E, T)和产生式T→F可以得到单位对(E, F)
(E, F)和产生式F→I可以得到单位对(E, I)
(T, T)和产生式T→F可以得到单位对(T, F)
(T, F)和产生式F→I可以得到单位对(T, I)
(F, F)和产生式F→I可以得到单位对(F, I)
所以这个文法一共有10个单位对。
去除一个文法的所有单位产生式，
所以继续上面那个例子，可以得到一个去除单位产生式的文法G1的产生式构造过程如下：
最后得到的产生式如下：
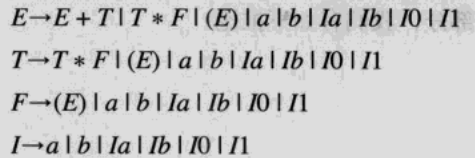
简化CFG
把一个CFG简化成为一个没有无用符号、ε产生式或者单位产生式的CFG，可以使用下面将上述步骤按照下面这个比较可靠的顺序执行：
- 去除ε产生式。
- 去除单位产生式。
- 去除无用符号。
乔姆斯基范式
任何非空且不含ε的CFL都有特殊形式的文法G，G中所有的产生式都属于以下两个简单的形式之一：
- A→BC，其中A，B和C都是变元，或者
- A→α，其中A是变元。α是终结符。
更进一步，G没有无用符号。这样的文法称为乔姆斯基范式(Chomsky Normal Form, CNF)。
将CFG转换成CNF
给定一个简化过后的上下文无关文法CFG，经过下面两个步骤可将其转换成CNF。
下面给出一个将CFG转换成CNF的例子：
将一个CFG替换成为CNF的好处：
- 去除了冗余
- 可以通过比较两个文法的产生式来确定它们是否相等
- 将语法生成树变成二分树
上下文无关语言的泵引理
对于上下文无关语言CFL，也有一个泵引理，可用来证明给定的一个语言L，L不是上下文无关语言：
下面给出一个泵引理应用的例子：
上下文无关语言的封闭性
上下文无关语言的判定性问题
给定一个上下文无关语言L，判定下面两个问题：
- L是否等于Ø
- 字符篡w是否属于L
使用CYK算法：
关于CYK算法，下面这个链接给出了详细的说明和例子：
https://web.cs.ucdavis.edu/~rogaway/classes/120/winter12/CYK.pdf
上下文语言中无法决定的判断性问题
- 无法用算法判断一个文法是否是歧义的
- 无法用算法判断一个上下文无关语言是固有歧义的
- 无法判断两个上下文无关语言的交集是否为空集
- 无法判断两个上下文无关语言是否相等
- 无法判断一个上下文无关语言是否等于其字母表的星运算
