正则语言与有穷自动机

正则表达式的运算符

1、两个语言L和M的并，记作L∪M，是只属于L或属于只属于M，或者同时属于二者的串的集合。这个运算符有时也记作L+M。

　  

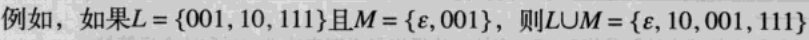
2、语言L和M的连接是以下形成的串的集合：取L中任意一个串，与M中任意一个串连接起来。一般用圆点或者根本不用任何运算符来表示两个语言的连接。

     

3、语言L的闭包（或星，或克林闭包），记作L*，表示用以下方式形成的串的集合：从L中取任意多个串，可能有重复（即可以多次选同一个串），把所有这些串连接起来。更形式化的说，L*是无穷的并U_i≥0Lⁱ，其中L⁰={ε}，L¹=L，对于i>1，L_i是i个L的连接。

    

正则语言

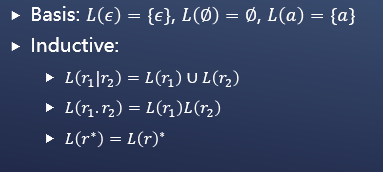
从RE到ε-NFA

对于正则语言：ε、Ø、a，对应的自动机依次如下

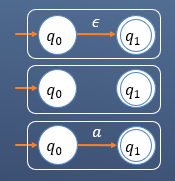
对于正则语言：R|S，对应的自动机如下

对于正则语言：R.S，对应的自动机如下

对于正则语言：R*，对应的自动机如下

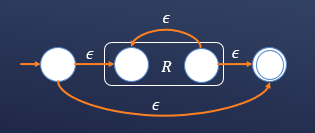
 下面给出一个例子：

将RE转换成ε-NFA后，可以按照下面的路径将ε-NFA转换成为DFA

RE→ε-NFA→NFA→DFA

从DFA到RE

可以通过状态消除的方法将一个FA转换成为RE，状态消除的方法如下：

合并：

消除顺序状态：

消除循环状态：

 

下面给出一个例子：

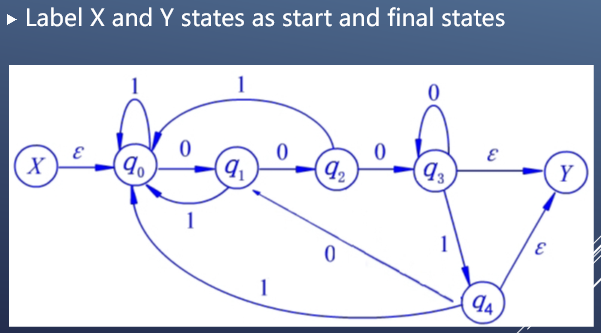
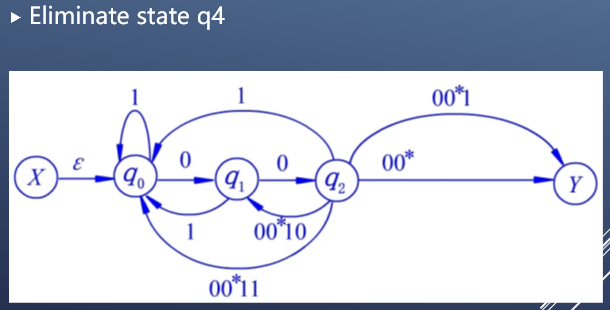
从NFA到正则文法

正则文法：

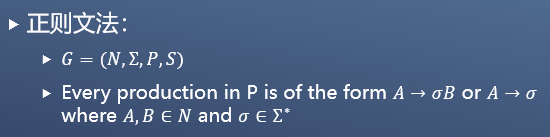
在前面的博客也有给出文法的定义，在这里，N是指非终止符号集，Σ是指终止符号集。

一个语言L能够被NFA接受，当且仅当这个语言有一个正则文法。

从一个NFA构造出一个等价的正则文法：

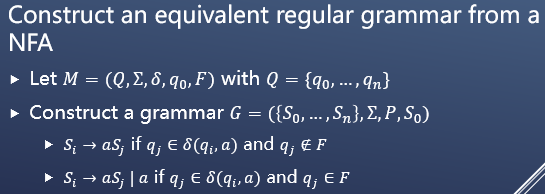
下面给出一个例子：

证明一个语言是正则语言

如果能构造出一个接受该语言的有限状态自动机，则是正则语言。

证明一个语言不是正则语言

如果语言L不满足泵引理，则不是正则语言。

泵引理的定义，其中n是一个与语言L相关的常数。

也就是说，我们总能在离w的开始处不太远的地方找到一个非空的串y，然后可以把它作为“泵”，也就是说，重复y任意多次，或者去掉它（k=0的情况），而所得到的结果串依然属于L。

下面给出一个例子：

DFA的最小化 - 填表算法

算法步骤：

下面给出一个例子，将下面的DFA最小化：

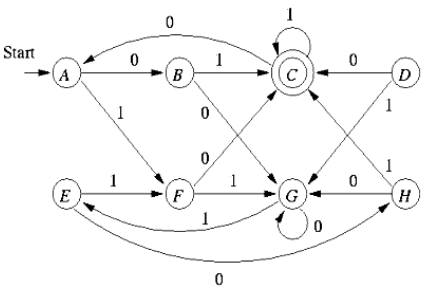
第一步，画一个表，然沿对角线画一条线，将对角线以上的部分丢掉（这是因为一个完整的表是沿对角线对称的），同时也要丢掉对角线上的部分，因为对任意的(q, q)，不可能有q属于F并且q不属于F。

第二步，将包含终止状态的状态对打上标记，如下

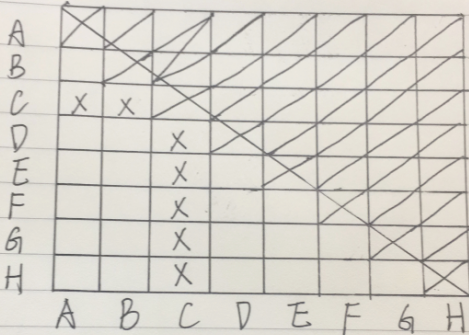
第三步，在状态转换图中找出所有与终止状态相邻的状态。依次检查这些状态，使用上述填表算法进行检查，标记上符合要求的状态对。检查完毕后，再向外扩张，直到每个状态对都被检查过为止。

 

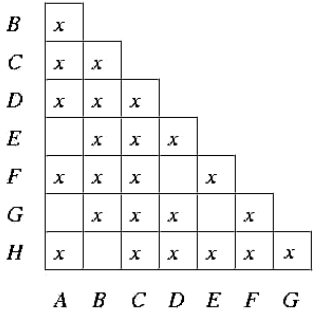
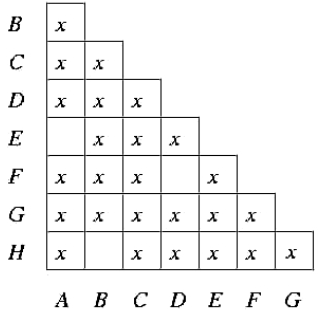
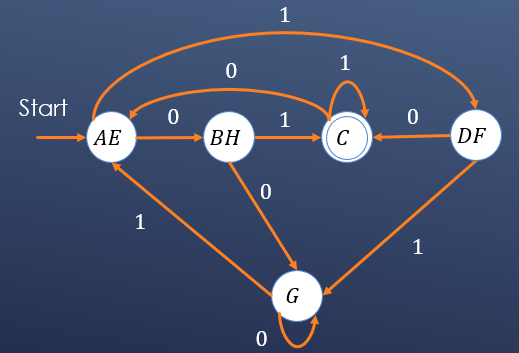
将所有等价的状态进行合并，即可得到最小化的DFA：

正则语言的封闭性

判定性问题

• 给定一个字符串w和正则语言L，判断w是否属于L

• 给定一个正则语言L，判断L是否为空

• 给定两个正则语言L₁和L₂，判断L₁是否等于L₂