有穷自动机
概述
有穷自动机有一组状态及其控制，响应外部的“输入”，“控制”从状态移动到状态。各类有穷自动机之间的关键区别之一，在于控制究竟是“确定的”还是“非确定的”，前者意味着在任何时候自动机不能处在一种以上的状态中，后者意味着自动机能同时储在几种状态中。
确定型有穷自动机（DFA）
通常同一个五元组来讨论DFA:
A=(Q,Σ,δ,q0,F)
其中A表示DFA的名称，Q是状态集合，Σ是输入符号的集合，δ是转移函数，q0是初始状态，F是接收状态的集合。
例：
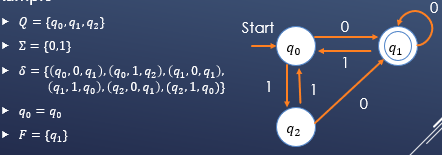
其中同心圆表示的是终止状态
确定的有限自动机的转换表表示法：
其中“→”符号标记的是起始状态，“*”标记的是终止状态。
DFA的扩展转移函数
DFA接受的语言
需要注意的是，有限状态自动机每种状态下接受的输入应该考虑到每一种可能的符号，即使实际的语言并不会在某种状态下产生某个符号，也应该设计一个死锁来接受该种符号。
下例中，状态D就是一种死锁状态：
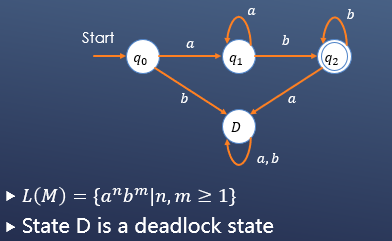
设计能接受某种语言的自动机时，第一步应该考虑的直接从起始状态进入终止状态的情况，然后依次考虑每种状态能进入终止状态的情况。
不确定的有限状态自动机（NFA）
这里的2Q表示Q的幂集
例如：
也就是说，不确定有限状态自动机中的一个状态接收同一个输入可能会跳转到不同的状态，并且支持跳转空状态。
NFA的扩展转移函数
可以发现，DFA的扩展转移函数和NFA的扩展转移函数的区别在于：DFA的扩展转移函数的右边是一个确定的状态，而NFA的扩展转移函数的右边是一个状态的集合，而这个集合种可以有多个状态也可以是一个空集。
NFA接受的语言
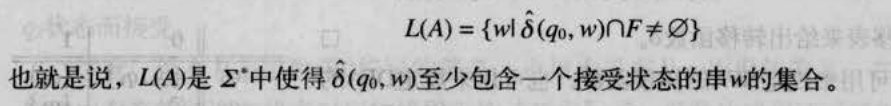
例如：
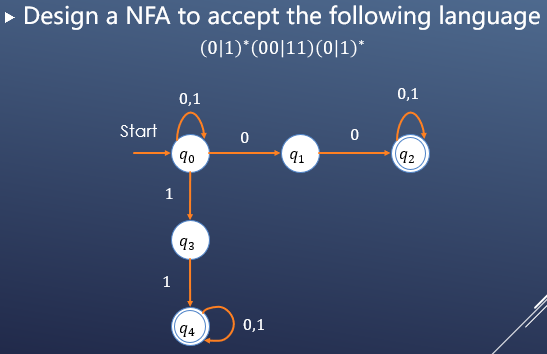
通过子集构造将NFA转化成DFA
当将NFA转化成DFA的时候，DFA的状态转移函数的右边是一个集合，不过这依然是一个确定的状态，它是这样的一个状态：由NFA的状态集合而构成的一个确定的状态。换句话说，DFA的状态集合是NFA的状态集合的子集的集合。
下图是一个NFA的状态迁移图：
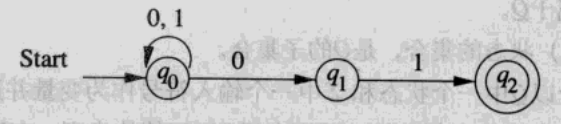
子集构造：
然后根据上述的子集构造方法构造NFA的完整子集构造。因为NFA有3种状态{q0, q1, q2}，所以完整的子集构造产生一个带有23=8种状态的DFA，对应于这三种状态的所有子集合。下图是这8中状态的状态转移表。
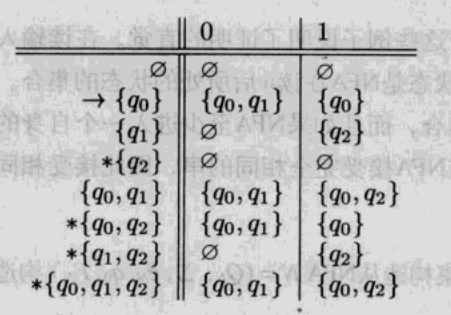
显然，对于上面这8种状态，从状态{q0}开始，只能到达{q0}、{q0, q1}、和{q0, q2}。其余5种状态都是从初始状态不可达的，也都可以不出现在表中。
进行了子集构造后，去除多余的状态即可得到这样的一个DFA，它与上面的NFA等价：
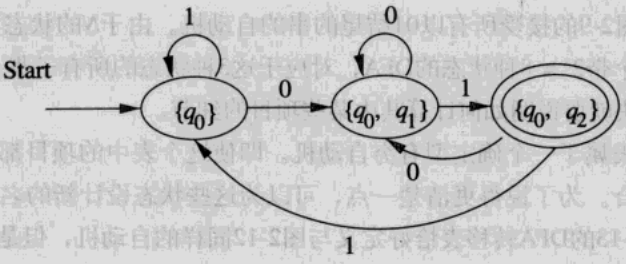
带空迁移的有限自动机（ε-NFA）
例如：
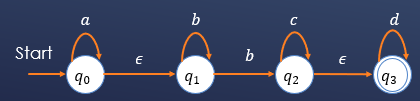
也就是说，带空迁移的有限状态自动机支持输入空符号进行状态迁移。
ε闭包
非形式化的定义：顺着所有从状态q出发带ε标记的转移来求状态q的ε的闭包。但当顺着ε到达其他状态后，再从这些状态发出ε转移，依此类推，最终求出顺着箭弧都带ε标记的任何路径从q可达的任何每个状态。
而其形式化的定义如下：
ε-NFA的扩展转移
ε-NFA接受的语言
与NFA一样，如果一个语言产生的句子中存在一条能从起始状态到达终止状态的路径，则称这种语言是ε-NFA接受的语言，记为：
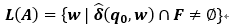
显然，ε-NFA和NFA是等价的。对于一个ε-NFA，依次讨论每种状态下接收非空符号的状态迁移情况，可以构造出一个NFA。
