简单线段树
一、什么是线段树?
-
线段树是怎样的树形结构?
线段树是一种二叉搜索树,每个结点都存储了一个区间,也可以理解成一个线段,你要从这些线段上进行搜索操作得到你想要的答案。
-
线段树能够解决什么样的问题?
线段树的适用范围很广,可以在线维护修改以及查询区间上的最值,求和。
需要注意的是,线段树只可以维护满足结合律的信息。
对于线段树来说,每次更新以及查询的时间复杂度为 \(O(\log n)\)。
-
线段树和其他 \(\texttt{RMQ}\) 算法的区别
常用的解决 \(\texttt{RMQ}\) 问题有 \(\texttt{ST}\) 表,二者预处理时间都是 \(O(n\log n)\)。
但二者的区别在于线段树支持在线更新值,而 \(\texttt{ST}\) 表不支持在线操作。
二、线段树的原理
线段树之所以称为“线段”树,是因为它的节点维护的信息是一个线段(即一个区间)的信息,而一个节点的两个儿子维护的信息是将当前节点维护线段(区间)分成两个线段,分别维护两个分成的线段(即子区间)的信息。
而线段树的精髓在于:根据结合律,通过儿子节点(子区间)的信息合并得到更大区间的信息。
三、线段树的基本操作
1. 建树
建树包括三个要点:结点存什么,结点下标是什么,如何建树。
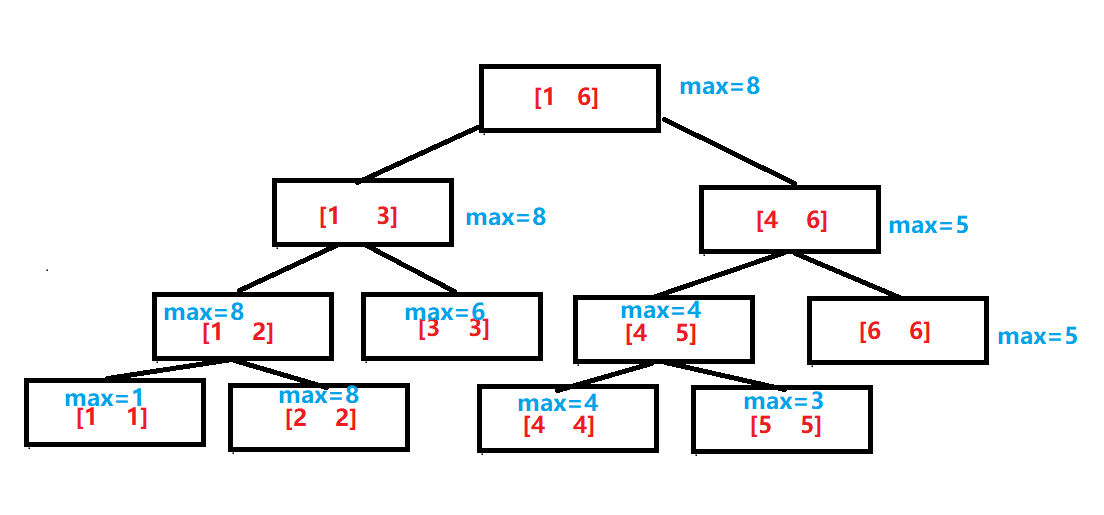
上图是关于 \(a[1\cdots6] = \{1,8,6,4,3,5\}\) 的区间最大值线段树,其中红色数字代表区间,蓝色数字代表当前区间最值。
- 节点存什么
可以发现,每个叶子结点的值就是数组的值,每个非叶子结点的度都为二,且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。
- 结点下标是什么
接着,我们采用完全二叉树的存储方法。即对于一个父节点 \(i\) 来说,它的左右儿子分别为 \(2i,2i+1\)。
- 如何建树
故此,在建树的时候,空间要开到 \(4n\) 以防止 RE。
建树时每次递归就要先判断 \(l\) 是否等于 \(r\),等于就说明是叶子节点,也就是区间是 \([l,l]\),直接赋值成 \(a[l]\),再返回。
否则就递归构造左儿子结点和递归构造右儿子结点,最后更新父节点。
inline void PushUp(int x) {
sum[x] = sum[x << 1] + sum[x << 1 | 1];
}//由于结合律,所以根据两儿子的信息可以合并成父亲的信息
inline void Build(int l, int r, int x) {
if(l == r) {
sum[x] = a[l];
return ;
}
int mid = l + r >> 1;
Build(l, mid, x << 1);
Build(mid + 1, r, x << 1 | 1);
PushUp(x);
}
(注意,示例代码均为线段树 1 代码)
2、区间查询
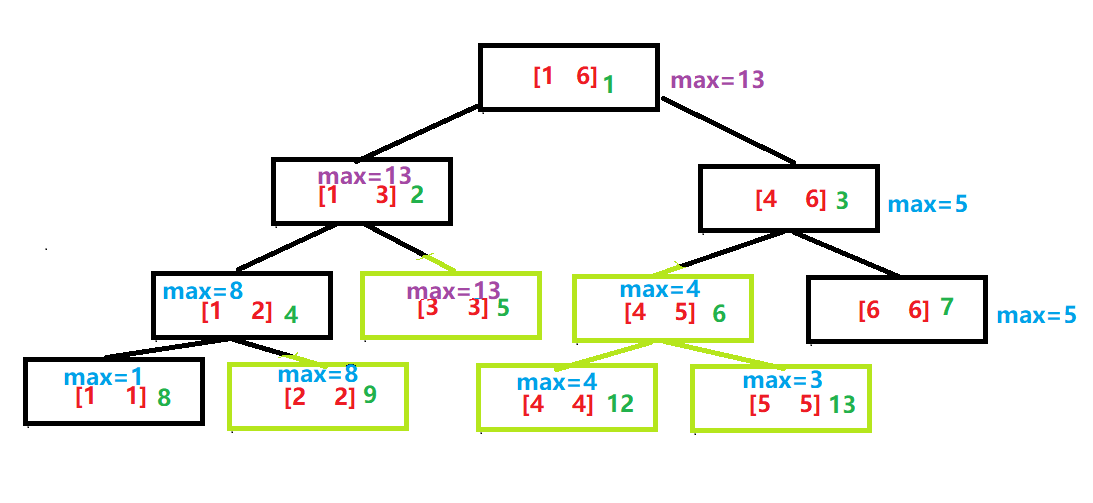
我们继续观察这棵线段树。
现在我要查询 \([2,5]\) 区间的最值,如何处理呢?
显然,此区间无法直接通过某一个节点的值直接求出;那么我们来看看有哪些区间被此区间包含。
共有 \(5\) 个区间(黄色部分),而且我们可以发现 \([4,5]\) 这个区间已经包含了两个子树的信息(\([4,4],[5,5]\)),所以我们需要查询的区间只有三个,分别是 \([2,2],[3,3],[4,5]\)。
我们还是从根节点开始往下递归,如果当前结点是被要查询的区间包含了的,则返回这个结点的信息,这样从根节点往下递归,时间复杂度也是 \(O(\log n)\)。
inline int Query(int L, int R, int l, int r, int x) {
if(L <= l && r <= R) return sum[x];
int mid = l + r >> 1;
int ans = 0;
if(L <= mid) ans += Query(L, R, l, mid, x << 1);
if(R > mid) ans += Query(L, R, mid + 1, r, x << 1 | 1);
return ans;
}
3、单点修改
从根节点递归去找 \(val\),找到了就返回,并再返回的一路上不断更新其父节点的信息即可。
基本等于二分查找。
(代码不用给了吧)
4、区间修改——懒标记(Lazytag)
由于线段树需要支持区间修改,所以我们需要引入懒标记,使修改在 \(\log n\) 的时间复杂度内完成。
懒标记的作用是记录当前区间已经修改,但子区间并未修改的信息。
由于我们虽然修改了当前区间的信息,但并未修改子区间的信息,所以我们需要记录懒标记,并在需要递归到子区间之前将懒标记下推到子区间。
设当前结点对应区间 \([l, r]\),待更新区间 \([a, b]\)。
当 \(a ≤ l ≤ r ≤ b\),即 \([l, r]∈[a,b]\) 时,不再向下更新,仅更新当前结点,并在该结点加上懒标记,当必须得更新/查询该结点的左右子结点时,再利用懒标记的记录向下更新(pushdown)——懒标记也要向下传递,然后移除该结点的懒标记。

我们仍然观察这棵线段树。
现在我要让 \([1,3]\) 集体加一。那么从根节点出发,即区间 \([1,6]\),发现这个区间并不是 \([1,3]\) 的“子集”,所以往下递归。下移到左子树 \([1,3]\),发现这个区间已经是 \([1,3]\) 的“子集” 了,那么我们在这个节点上加一个 lazytag,即 \(lazy[2]=1\),然后更新当前值。注意再递归回去的时候顺便更新根节点的值。
现在我要让 \([2,3]\) 集体加二。
依然先从根节点出发。转移到它的左子树 \([1,3]\)。
这一次,我们发现这个点无法满足是 \([2,3]\) 的“子集”,那么接着向下递归。但是,在递归之前,我们要将此节点的 lazytag 下传。即 \(lazy[4]+1,lazy[5]+1\),然后把当前 lazytag 清零,即 \(lazy[2]=0\)。
继续,下传到 \([1,2]\),同上,下传 lazytag 和清空;下传到 \([3,3]\),发现 \([3,3]\) 是 \([2,3]\) 的“子集”,那么结束。
最后,由 \([1,2]\) 下传到 \([2,2]\),修改结束。
inline void PushDown(int x, int ln, int rn) {
if(add[x]) {
add[x << 1] += add[x];
add[x << 1 | 1] += add[x];
sum[x << 1] += add[x] * ln;
sum[x << 1 | 1] += add[x] * rn;
add[x] = 0;
}
}
inline void Update(int L, int R, int C, int l, int r, int x) {
if(L <= l && R >= r) {
sum[x] += C * (r - l + 1);//注意由于是求和,所以当前节点加的是包含区间长度*价值
add[x] += C;
return ;
}
int mid = l + r >> 1;
PushDown(x, mid - l + 1, r - mid);
if(L <= mid) Update(L, R, C, l, mid, x << 1);
if(R > mid) Update(L, R, C, mid + 1, r, x << 1 | 1);
PushUp(x);
}
5、区间查询(lazytag)
在前面的基础上加上 pushdown 即可。
四、例题
模板题。包括了区间修改和区间查询。代码在上面已经给出。
显然不可以直接用线段树维护,因为区间加的不是同一个值。
再看一下题目发现,题目给出的是一个等差数列,也就是说,累加序列的相邻两项的差是相等的。
不难想到差分。这样我们就可以把区间加的数变为相等的数,可以用线段树维护了。再看查询是单点查询,也就是查询差分数组的前缀和,线段树普通区间查询即可。
这题乍一看和线段树没什么关系,疑似是可以直接计算的。
但是我们会发现,如果直接模拟题意,高精会爆空间,如果写逆元这题模数不是质数,直接计算肯定不行。
所以再仔细看题目:
对于每一个类型 1 的操作至多会被除一次
也就是说,当计算除法时,就相当于少乘一个乘数,即每次除法操作就相当于将某乘数变成 \(1\)。
而每个乘法操作就是多一个乘数,即把乘以一个 \(1\) 改为乘以某个数。
而输出的数就是所有乘数之积,包括 \(1\) 在内。
单点修改,区间查询,用线段树维护区间积即可。
小清新线段树。
开方有 \(2\) 个特殊值:\(0,1\)。对于这两个数,开方无实际意义。
题目中给到的 \(a_i\) 值是 \(10^{12}\),在开 \(6\) 次方后就会变成 \(1\)。
所以线段树中再记录区间最大值,当最大值是 \(1\) 时,就可以不用开方。
经典括号问题。
对于一个括号串,我们有一条基本规则:
对于任意前缀,左括号数 \(\geq\) 右括号数,且两括号总数相等。
满足此条件,即可称此括号串为合法括号串。
在本题中,我们不妨设左括号为 \(1\),右括号为 \(-1\),普通字符为 \(0\)。这样的话,刚才的判断条件就转化成了如下式子。
其中 \(sum_i\) 表示前缀和数组。
然后再来观察这样的定义下“最深嵌套”是什么。
从左往右每出现一个左括号就会使嵌套层数增加,而每出现一个右括号就会使嵌套层数减少,因此最深嵌套层数就是最大的前缀和。
线段树维护区间和,区间 min/max 即可。
这题有区间修改,显然是线段树一类的数据结构来维护。
题面提到,要求连续的空房长度,显然需要用到较为复杂的维护。
考虑维护三个值:区间最长连续空房长度,区间最长连续空房前缀,区间最长连续空房后缀。
显然上传的时候,区间最长空房可以根据儿子的区间最长空房以及左儿子的最长后缀+右儿子的最长前缀的最大值转移。
区间最长前缀可以根据左儿子最长前缀(如果左儿子全是空房可以根据左儿子区间长度+右儿子最长前缀)转移。
区间最长后缀同理可得。
然后我们考虑如何求得长度 \(\geq x\) 的最左区间的左端点。
方法 1:考虑二分右端点,比较 \([1,mid]\) 区间的最长空房长度与 \(x\) 的大小。
方法 2:递归查找,判断线段树当前区间左儿子最长空房与 \(x\) 的大小,如果左儿子最长空房 \(≥x\),就递归左儿子;如果左儿子最长后缀+右儿子最长前缀 \(≥x\),就返回左儿子最长后缀的开始位置;否则递归右儿子。
方法 1 时间复杂度为 \(O(n \log^2 n)\),方法 2 时间复杂度为 \(O(n \log n)\),均可通过此题。
SP1043 GSS1 - Can you answer these queries I
经典线段树维护最大区间子段和,P4513 小白逛公园 的弱化版。
定义:
struct kkk{
int val; //表示该区间的权值和
int left; //表示该区间的前缀最大和
int right; //表示该区间的后缀最大和
int middle; //表示该区间的最大子段和
kkk(){val=left=right=middle=0;} //清0
}tree[maxn];
大家都应知道,线段树基本原理,那么最大子段和放在线段树上,其实就是两个区间的合并时怎么将区间关系,pushup 区间的问题。
下面给出两个区间合并的方式:合并的区间为 \(res\)
合并保证 \(x\) 是左区间,\(y\) 是右区间,\(x,y\) 相邻。
首先是 \(val\) 的合并,很简单,区间 \(x\) 的 \(val+\) 区间 \(y\) 的 \(val\)。
res.val=x.val+y.val;
然后是 \(left\) 的合并,前缀最大和只有两种情况,要么是 \(x\) 区间的前缀最大和,要么是 \(x\) 的权值和 \(y\) 的前缀最大和。结果是这两种情况的 \(max\) 值。
那么 \(right\) 的合并也差不多,要么是 \(y\) 区间的后缀最大和,要么是 \(y\) 的权值 \(+x\) 的后缀最大和。
至于 \(middle\) 就分几种情况:
1.\(x\) 区间的 \(middle\)
2.\(y\) 区间的 \(middle\)
3.\(x\) 区间的后缀最大和 \(+y\) 区间的前缀最大和
答案即为 \(middle\)。
GSS3 - Can you answer these queries III
带修区间最大子段和。
只要在 GSS1 的基础上加上单点修改即可。基本和小白逛公园一致。
简单的线段树模板题。
使用两个 tag,t1 表示区间赋值,t2 表示区间加。加法打标记时若赋值标记存在则直接给赋值标记加上对应值,不修改加标记,否则修改加标记;打赋值标记时先清空加标记即可。
在实现时,区间赋值和区间加的两个 update 函数找节点的过程是相同的,区别只在 make_tag 过程。因此可以把这两个操作的 update 函数写成一个,另加一个参数表示操作类型是赋值还是加法即可。
我们令灯关着的时候是 \(0\),开着的时候是 \(1\)。
初始所有数都是 \(0\)。
题目要求支持两种操作,一种是区间异或 \(1\),还有一种是区间查询1的个数。
考虑到所有数中只有 \(0\) 和 \(1\)。
所以查询可以改为查询区间和。
区间异或 \(1\) 也可以从区间和的角度取考虑问题。
假设我们有 \(k\) 个 \(1\),区间长度为 \(l\)。
那么显然取反后有 \(l-k\) 个 \(1\)。
所以 \(tree_x = (r-l+1)-tree_x\)。
我们把方差公式展开。
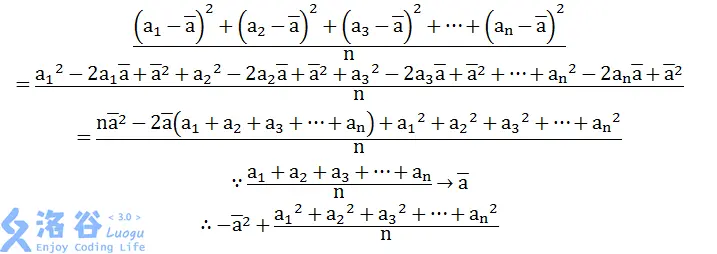
显然区间平均值是好求的,那么我们重点观察这个区间平方和怎么求。
设区间加了 \(k\),
那么再次展开平方。
\(sum_2 = sum_2 + 2k\cdot sum_1 + nk^2\)
这个就可以线段树维护了。

