NOIP2024加赛8
NOIP2024加赛8
题目来源： 2023NOIP A层联测32
\(T1\) HZTG5781. flandre \(100pts\)
-
先将 \(\{ a \}\) 升序排序并去重后，由调整法可知选取的数一定是一段后缀。
-
正数的贡献肯定是无脑全加上，难点在于负数中多次出现的数的选择。
-
不妨钦定答案序列中选择的最小的数，通过需要加入这个数进一步可归纳出在原序列上也是一段后缀。
点击查看代码
ll cnt[2000010],pre[2000010],suf[2000010]; pair<ll,ll>a[1000010]; vector<pair<ll,ll> >z,f; int main() { freopen("flandre.in","r",stdin); freopen("flandre.out","w",stdout); ll n,k,ans=0,sum=0,id=-1,i; scanf("%lld%lld",&n,&k); for(i=1;i<=n;i++) { scanf("%lld",&a[i].first); a[i].second=i; cnt[a[i].first+1000000]++; if(a[i].first>=0) { z.push_back(a[i]); } else { f.push_back(a[i]); } } for(i=1000000;i<=2000000;i++) { pre[i]=pre[i-1]+cnt[i]; } for(i=2000000;i>=0;i--) { suf[i]=suf[i+1]+cnt[i]; } sort(z.begin(),z.end()); sort(f.begin(),f.end(),greater<pair<ll,ll>>()); for(i=0;i<z.size();i++) { sum+=z[i].first+pre[z[i].first+1000000-1]*k; } ans=sum; for(i=0;i<f.size();i++) { sum+=f[i].first+suf[f[i].first+1000000+1]*k; if(ans<sum) { ans=sum; id=i; } } printf("%lld %lld\n",ans,z.size()+id+1); for(i=id;i>=0;i--) { printf("%lld ",f[i].second); } for(i=0;i<z.size();i++) { printf("%lld ",z[i].second); } return 0; }
\(T2\) HZTG5782. meirin \(20pts\)
-
部分分
- \(20pts\) ：暴力。
点击查看代码
const ll p=1000000007; ll a[500010],sum[500010],b[500010]; struct SMT { struct SegmentTree { ll len,sum,lazy; }tree[2000010]; #define lson(rt) (rt<<1) #define rson(rt) (rt<<1|1) void pushup(ll rt) { tree[rt].sum=(tree[lson(rt)].sum+tree[rson(rt)].sum)%p; } void build(ll rt,ll l,ll r) { tree[rt].len=r-l+1; if(l==r) { tree[rt].sum=b[l]; return; } ll mid=(l+r)/2; build(lson(rt),l,mid); build(rson(rt),mid+1,r); pushup(rt); } void pushlazy(ll rt,ll lazy) { tree[rt].sum=(tree[rt].sum+tree[rt].len*lazy%p)%p; tree[rt].lazy=(tree[rt].lazy+lazy)%p; } void pushdown(ll rt) { if(tree[rt].lazy!=0) { pushlazy(lson(rt),tree[rt].lazy); pushlazy(rson(rt),tree[rt].lazy); tree[rt].lazy=0; } } void update(ll rt,ll l,ll r,ll x,ll y,ll val) { if(x<=l&&r<=y) { pushlazy(rt,val); return; } pushdown(rt); ll mid=(l+r)/2; if(x<=mid) { update(lson(rt),l,mid,x,y,val); } if(y>mid) { update(rson(rt),mid+1,r,x,y,val); } pushup(rt); } ll query(ll rt,ll l,ll r,ll x,ll y) { if(x<=l&&r<=y) { return tree[rt].sum; } pushdown(rt); ll mid=(l+r)/2; if(y<=mid) { return query(lson(rt),l,mid,x,y); } if(x>mid) { return query(rson(rt),mid+1,r,x,y); } return (query(lson(rt),l,mid,x,y)+query(rson(rt),mid+1,r,x,y))%p; } }T; ll ask(ll n) { ll ans=0; for(ll i=1;i<=n;i++) { for(ll j=i;j<=n;j++) { ans+=(sum[j]-sum[i-1])%p*T.query(1,1,n,i,j)%p; ans%=p; } } return ans; } int main() { freopen("meirin.in","r",stdin); freopen("meirin.out","w",stdout); ll n,m,l,r,k,i; scanf("%lld%lld",&n,&m); for(i=1;i<=n;i++) { scanf("%lld",&a[i]); sum[i]=sum[i-1]+a[i]; } for(i=1;i<=n;i++) { scanf("%lld",&b[i]); } T.build(1,1,n); for(i=1;i<=m;i++) { scanf("%lld%lld%lld",&l,&r,&k); T.update(1,1,n,l,r,(k+p)%p); printf("%lld\n",ask(n)); } return 0; } -
正解
- 尝试拆式子。
- 观察到 \(\{ a \}\) 始终不变，先将 \(\{ a \}\) 提出来，原式等价于 \(\sum\limits_{l=1}^{n}\sum\limits_{r=l}^{n}\sum\limits_{i=l}^{r}(b_{i} \times \sum\limits_{j=l}^{r}a_{j})\) 。
- 待定系数设原式等价于 \(\sum\limits_{i=1}^{n}b_{i}k_{i}\) ，其中 \(k_{i}=\sum\limits_{j=1}^{n}x_{i,j}a_{j}\) 。此时 \([l,r]\) 增加 \(d\) 对答案的影响就是 \(d\sum\limits_{i=l}^{r}k_{i}\) 。
- 而 \(x_{i,j}\) 的实际含义是同时包含了 \(i,j\) 的区间个数，故有 \(x_{i,j}=\min(i,j) \times (n-\max(i,j)+1)\) ，故 \(k_{i}=\sum\limits_{j=1}^{i-1}j(n-i+1)a_{j}+\sum\limits_{j=i}^{n}i(n-j+1)a_{j}=-i\sum\limits_{j=1}^{n}ja_{j}+(n+1)\sum\limits_{j=1}^{i-1}ja_{j}+i(n+1)\sum\limits_{j=i}^{n}a_{j}\) 。前缀和预处理即可。
点击查看代码
const ll p=1000000007; ll a[500010],sum[500010][2],k[500010],b[500010]; int main() { freopen("meirin.in","r",stdin); freopen("meirin.out","w",stdout); ll n,m,l,r,ans=0,d,i; scanf("%lld%lld",&n,&m); for(i=1;i<=n;i++) { scanf("%lld",&a[i]); sum[i][0]=(sum[i-1][0]+a[i]*i%p)%p; sum[i][1]=(sum[i-1][1]+a[i])%p; } for(i=1;i<=n;i++) { scanf("%lld",&b[i]); k[i]=((n+1)*sum[i-1][0]%p+(sum[n][1]-sum[i-1][1]+p)%p*i%p*(n+1)%p-i*sum[n][0]%p+p)%p; ans=(ans+k[i]*b[i]%p)%p; k[i]=(k[i]+k[i-1])%p; } for(i=1;i<=m;i++) { scanf("%lld%lld%lld",&l,&r,&d); d=(d+p)%p; ans=(ans+(k[r]-k[l-1]+p)%p*d%p)%p; printf("%lld\n",ans); } return 0; }
\(T3\) HZTG5783. sakuya \(50pts\)
-
部分分
- \(40pts\)
- 将期望的式子展开，等价于求 \(\frac{\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}d(a_{i},a_{j})(m-1)!}{m!}=\frac{\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{m}d(a_{i},a_{j})}{m}\) ，树状数组维护区间修改、单点查询。时间复杂度为 \(O(qm^{2}\log n)\) 。
- \(50pts\)
- 考虑维护 \(dis_{1,x}\) 在答案中的系数，可以 \(O(m^{2} \log n)\) 或 \(O(n \log n+m^{2})\) 预处理。然后前缀和更新后 \(O(1)\) 询问即可。
点击查看代码
const ll p=998244353; struct node { ll nxt,to,w; }e[1000010]; ll head[1000010],a[1000010],siz[1000010],fa[1000010],dep[1000010],dis[1000010],son[1000010],top[1000010],dfn[1000010],out[1000010],pos[1000010],c[1000010],sum[1000010],tot=0,cnt=0; void add(ll u,ll v,ll w) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; e[cnt].w=w; head[u]=cnt; } ll qpow(ll a,ll b,ll p) { ll ans=1; while(b) { if(b&1) { ans=ans*a%p; } b>>=1; a=a*a%p; } return ans; } void dfs1(ll x,ll father) { siz[x]=1; fa[x]=father; dep[x]=dep[father]+1; for(ll i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=father) { dis[e[i].to]=(dis[x]+e[i].w)%p; dfs1(e[i].to,x); siz[x]+=siz[e[i].to]; son[x]=(siz[e[i].to]>siz[son[x]])?e[i].to:son[x]; } } } void dfs2(ll x,ll id) { top[x]=id; tot++; dfn[x]=tot; pos[tot]=x; if(son[x]!=0) { dfs2(son[x],id); for(ll i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=fa[x]&&e[i].to!=son[x]) { dfs2(e[i].to,e[i].to); } } } out[x]=tot; } ll lca(ll u,ll v) { while(top[u]!=top[v]) { if(dep[top[u]]>dep[top[v]]) { u=fa[top[u]]; } else { v=fa[top[v]]; } } return dep[u]<dep[v]?u:v; } int main() { freopen("sakuya.in","r",stdin); freopen("sakuya.out","w",stdout); ll n,m,inv,q,u,v,w,x,ans=0,i,j; scanf("%lld%lld",&n,&m); inv=qpow(m,p-2,p); for(i=1;i<=n-1;i++) { scanf("%lld%lld%lld",&u,&v,&w); add(u,v,w); add(v,u,w); } dfs1(1,0); dfs2(1,1); for(i=1;i<=m;i++) { scanf("%lld",&a[i]); c[dfn[a[i]]]=2*m%p; } for(i=1;i<=m;i++) { for(j=1;j<=m;j++) { c[dfn[lca(a[i],a[j])]]=(c[dfn[lca(a[i],a[j])]]-2+p)%p; } } for(i=1;i<=n;i++) { sum[i]=(sum[i-1]+c[i])%p; ans=(ans+dis[pos[i]]*c[i]%p)%p; } scanf("%lld",&q); for(i=1;i<=q;i++) { scanf("%lld%lld",&u,&x); if(u==1) { ans=(ans+(sum[out[u]]-sum[dfn[u]]+p)%p*x%p)%p; } else { ans=(ans+x*c[dfn[u]]%p)%p; x=x*2%p; ans=(ans+(sum[out[u]]-sum[dfn[u]]+p)%p*x%p)%p; } printf("%lld\n",ans*inv%p); } return 0; } - \(40pts\)
-
正解
- 因处理出每个点能作为多少个特殊点对的 \(\operatorname{LCA}\) 难以快速预处理，只能另寻他法。
- 考虑维护每条边 \((u,v,w)\) 在答案中的系数 \(cnt_{u,v}\) ，直接树形 \(DP\) 讨论一条边将树分成的两个部分的贡献合并即可。
点击查看代码
const ll p=998244353; struct node { ll nxt,to,w; }e[1000010]; ll head[1000010],a[1000010],siz[1000010],f[1000010],cnt=0,ans=0,m; void add(ll u,ll v,ll w) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; e[cnt].w=w; head[u]=cnt; } ll qpow(ll a,ll b,ll p) { ll ans=1; while(b) { if(b&1) { ans=ans*a%p; } b>>=1; a=a*a%p; } return ans; } void dfs1(ll x,ll fa) { for(ll i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=fa) { dfs1(e[i].to,x); siz[x]+=siz[e[i].to]; } } f[x]=(f[x]+2*siz[x]*(m-siz[x])%p)%p; } void dfs2(ll x,ll fa) { for(ll i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=fa) { ans=(ans+2*siz[e[i].to]*(m-siz[e[i].to])%p*e[i].w%p)%p; f[x]=(f[x]+2*siz[e[i].to]*(m-siz[e[i].to])%p)%p; dfs2(e[i].to,x); } } } int main() { freopen("sakuya.in","r",stdin); freopen("sakuya.out","w",stdout); ll n,inv,q,u,v,w,x,i; scanf("%lld%lld",&n,&m); inv=qpow(m,p-2,p); for(i=1;i<=n-1;i++) { scanf("%lld%lld%lld",&u,&v,&w); add(u,v,w); add(v,u,w); } for(i=1;i<=m;i++) { scanf("%lld",&a[i]); siz[a[i]]=1; } dfs1(1,0); dfs2(1,0); scanf("%lld",&q); for(i=1;i<=q;i++) { scanf("%lld%lld",&u,&x); ans=(ans+f[u]*x%p)%p; printf("%lld\n",ans*inv%p); } return 0; }
\(T4\) HZTG5784. 红楼 ~ Eastern Dream \(25pts\)
-
部分分
- \(25pts\) ：暴力。
点击查看代码
ll a[200010]; int main() { freopen("scarlet.in","r",stdin); freopen("scarlet.out","w",stdout); ll n,m,pd,l,r,k,ans=0,i,j; scanf("%lld%lld",&n,&m); for(i=1;i<=n;i++) { scanf("%lld",&a[i]); } for(j=1;j<=m;j++) { scanf("%lld%lld%lld",&pd,&l,&r); if(pd==1) { scanf("%lld",&k); for(i=1;i<=n;i++) { if((i-1)%l<=r) { a[i]+=k; } } } else { ans=0; for(i=l;i<=r;i++) { ans+=a[i]; } printf("%lld\n",ans); } } return 0; } -
正解
-
考虑根号分治。
-
当 \(x \le \sqrt{n}\) 时，分成的块数很多，但循环节长度小，设 \(add_{i,j}\) 表示下标 \(\mod i=j\) 时的增量，询问时枚举循环节计算整循环节的答案和散循环节的答案，前缀和加速即可。
-
当 \(x > \sqrt{n}\) 时，分成的块数很少，但循环节长度大，修改单次规模是 \(O(\sqrt{n})\) 的，但询问单次却只有 \(O(1)\) ，线段树或树状数组直接修改的时间复杂度为 \(O(n\sqrt{n}\log n)\)，无法接受。尝试 \(O(1)\) 区间加 \(O(\sqrt{n})\) 区间求和。
-
具体地，考虑维护修改导致的差分数组 \(\{ d \}\) ，询问 \([l,r]\) 的区间和等价于 \(\sum\limits_{i=l}^{r}a_{i}+\sum\limits_{i=l}^{r}\sum\limits_{j=1}^{i}d_{j}=\sum\limits_{i=l}^{r}a_{i}+(r-l+1)\sum\limits_{i=1}^{l-1}d_{i}+(r+1)\sum\limits_{i=l}^{r}d_{i}-\sum\limits_{i=l}^{r}d_{i}i\) 。然后就可以分块维护 \(d_{i},d_{i}i\) 即可。
-
题解的做法貌似有点麻烦了。
-
-
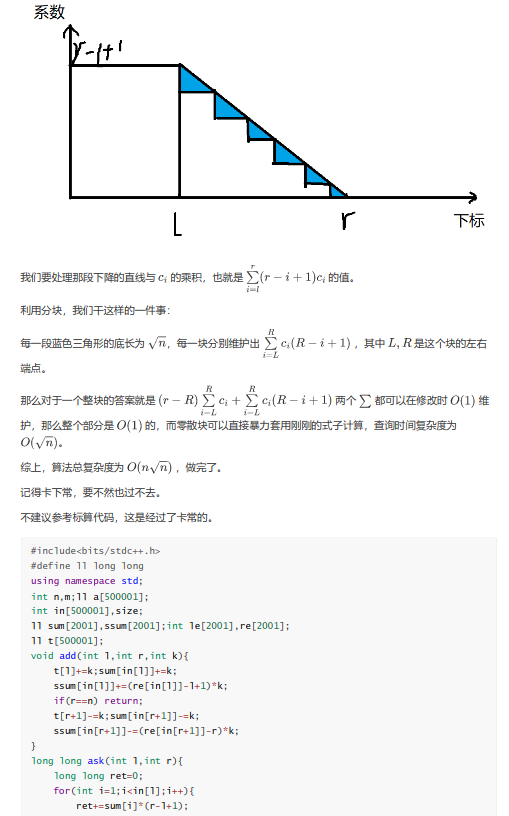
略带卡常，多交几发就行。
-
中途可能会炸
long long，但数据没卡且std也没开__int128_t，估计是因为int128_t对性能影响较大。
点击查看代码
int pos[200010],L[200010],R[200010],klen,ksum,n; ll a[200010],f[460][460],d[2][200010],sum[2][200010]; void init(int n) { klen=sqrt(n); ksum=n/klen; for(int i=1;i<=ksum;i++) { L[i]=R[i-1]+1; R[i]=R[i-1]+klen; } if(R[ksum]<n) { ksum++; L[ksum]=R[ksum-1]+1; R[ksum]=n; } for(int i=1;i<=ksum;i++) { for(int j=L[i];j<=R[i];j++) { pos[j]=i; } } } void update1(int p,int r,ll k) { ll sum=0; for(int i=0;i<=r;i++) { sum+=k; f[p][i]+=sum; } for(int i=r+1;i<=p;i++) { f[p][i]+=sum; } } void update3(int l,int r,ll k) { d[0][l]+=k; sum[0][pos[l]]+=k; d[1][l]+=k*l; sum[1][pos[l]]+=k*l; if(r<=n) { d[0][r+1]-=k; sum[0][pos[r+1]]-=k; d[1][r+1]-=k*(r+1); sum[1][pos[r+1]]-=k*(r+1); } } void update2(int p,int r,ll k) { for(int i=1;i<=n;i+=p) { update3(i,i+r,k); } } ll ask(int p,int pos) { return (pos/p)*f[p][p]+f[p][pos%p]; } ll query1(int l,int r) { ll ans=0; if(l==0) { for(int i=1;i<=klen;i++) { ans+=ask(i,r); } } else { for(int i=1;i<=klen;i++) { ans+=ask(i,r)-ask(i,l-1); } } return ans; } ll query2(int l,int r) { ll ans=0; for(int i=1;i<=pos[l-1]-1;i++) { ans+=sum[0][i]*(r-l+1); } for(int i=L[pos[l-1]];i<=l-1;i++) { ans+=d[0][i]*(r-l+1); } if(pos[l]==pos[r]) { for(int i=l;i<=r;i++) { ans+=d[0][i]*(r+1)-d[1][i]; } } else { for(int i=l;i<=R[pos[l]];i++) { ans+=d[0][i]*(r+1)-d[1][i]; } for(int i=pos[l]+1;i<=pos[r]-1;i++) { ans+=sum[0][i]*(r+1)-sum[1][i]; } for(int i=L[pos[r]];i<=r;i++) { ans+=d[0][i]*(r+1)-d[1][i]; } } return ans; } int main() { freopen("scarlet.in","r",stdin); freopen("scarlet.out","w",stdout); int m,pd,l,r,k,i; scanf("%d%d",&n,&m); for(i=1;i<=n;i++) { scanf("%lld",&a[i]); a[i]+=a[i-1]; } init(n); for(i=1;i<=m;i++) { scanf("%d%d%d",&pd,&l,&r); if(pd==1) { scanf("%d",&k); r=min(l-1,r); if(l<=klen) { update1(l,r,k); } else { update2(l,r,k); } } else { printf("%lld\n",query1(l-1,r-1)+query2(l,r)+a[r]-a[l-1]); } } return 0; } -
总结
- \(T2\) 因为之前看过题面且当时不会，遂赛时觉得肯定写不出来，对心态影响较大，感觉很难做到初三时原政治老师所说的“忘掉自己之前写过的所有题”。正式开题后约 \(40 \min\) 时 \(T1\) 的大样例在虚拟机上跑没过，码了个暴力发现也没过（赛后发现是因为虚拟机的巨大延迟导致编译的代码不是当前代码导致的）。此时已经 \(1.5h\) 过去了，看了眼后面的题加飞速写完 \(T2,T4\) 最低档暴力的部分分后又口胡了一个 \(T1\) 的假做法。在发现自己 \(3h\) 了相对分数仅有 \(0pts\) 时彻底破防了，因为 \(T3\) 有思路遂出去冷静下了后就回来写 \(T3\) 了，期间因为对根节点特判不当导致先后打的树状数组、线段树、暴力都没过第 \(2\) 个小样例，在已经准备摆烂时静态查错找到了错误，成功在最后半个小时从 \(5pts\) 救到了 \(50pts\) 。但全程 \(T4\) 的根号分治没来得及写，还算比较伤。
- 虚拟机大部分还原考场环境，让我们提前适应赛时虚拟机卡死的情况，被迫用 \(Geany\) 写了。
后记
- \(T1\) 第 \(4\) 个样例的输入文件因编码格式（至少 \(miaomiao\) 是这么说的）把 \(n,k\) 弄丢了。
- 赛时不知道怎么搞的把 \(PDF\) 题面炸没了。
本文来自博客园，作者：hzoi_Shadow，原文链接：https://www.cnblogs.com/The-Shadow-Dragon/p/18572893，未经允许严禁转载。
版权声明：本作品采用 「署名-非商业性使用-相同方式共享 4.0 国际」许可协议（CC BY-NC-SA 4.0） 进行许可。
