csp-s模拟12
csp-s模拟12

\(T1\) T2918. 小 h 的几何 \(100pts\)
-
对于任意三角形,均有其三条边的中点、三条高的垂足、三个顶点与垂心连线的中点,这九个点在一个圆上。
-
观察样例可知,对于单位圆上 \(\triangle ABC\) 的三个顶点 \(A(x_{a},y_{a}),B(x_{b},y_{b}),C(x_{c},y_{c})\) ,其九点圆圆心为 \(\Omega (A,B,C)=(\dfrac{x_{a}+x_{b}+x_{c}}{2},\dfrac{y_{a}+y_{b}+y_{c}}{2})\) 。
- 证明
-
直接构造坐标(从单位圆的角度考虑)
- 不妨只取三条边的中点参与计算,等价于求 \(D(\dfrac{x_{a}+x_{b}}{2},\dfrac{y_{a}+y_{b}}{2}),E(\dfrac{x_{a}+x_{c}}{2},\dfrac{y_{a}+y_{c}}{2}),F(\dfrac{x_{b}+x_{c}}{2},\dfrac{y_{b}+y_{c}}{2})\) 的外接圆圆心。
- 设 \(\Omega (A,B,C)=(x,y)\) 等价于求 \(\begin{cases} (x-\frac{x_{a}+x_{b}}{2})^{2}+(y-\frac{y_{a}+y_{b}}{2})^{2}=r^{2} \\ (x-\frac{x_{a}+x_{c}}{2})^{2}+(y-\frac{y_{a}+y_{c}}{2})^{2}=r^{2} \\ (x-\frac{x_{b}+x_{c}}{2})^{2}+(y-\frac{y_{b}+y_{c}}{2})^{2}=r^{2} \end{cases}\) ,又因为 \(x_{a}^{2}+y_{a}^{2}=x_{b}^{2}+y_{b}^{2}=x_{c}^{2}+y_{c}^{2}=(2r)^{2}=4r^{2}=1^{2}=1\) ,不难想到构造 \(\begin{cases} x=\frac{x_{a}+x_{b}+x_{c}}{2} \\ y=\frac{y_{a}+y_{b}+y_{c}}{2} \end{cases}\) 。
- 由中点三角形的相似性 \(\triangle ABC \backsim \triangle FED\) 和相似比等于 \(2\) ,不难得到 \(\triangle ABC\) 外接圆半径和 \(\triangle FED\) 外接圆半径的相似比也等于 \(2\) 。
- 好像这个结论不是很显然(从代数推导的角度可能会比较显然?),证明咕了。
- 由中点三角形的相似性 \(\triangle ABC \backsim \triangle FED\) 和相似比等于 \(2\) ,不难得到 \(\triangle ABC\) 外接圆半径和 \(\triangle FED\) 外接圆半径的相似比也等于 \(2\) 。
-
挂下题解做法。
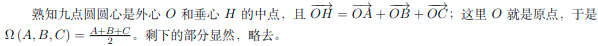
-
- 证明
-
统计 \((x_{i},y_{i})\) 作为 \(A,B,C\) 计算次数的贡献即可,拆开式子减小精度误差,有 \(\dbinom{n-i}{2}+\dbinom{i-1}{1}\dbinom{n-i}{1}+\dbinom{i-1}{2}=\dfrac{(n-i)(n-i-1)}{2}+(i-1)(n-i)+\dfrac{(i-1)(i-2)}{2}\) 。
点击查看代码
const double Pi=3.141592653589,mod=1000000000; int main() { freopen("geometry.in","r",stdin); freopen("geometry.out","w",stdout); ll n,i; double q,x,y,ansx=0,ansy=0; cin>>n; for(i=1;i<=n;i++) { cin>>q; x=cos(q/mod*Pi); y=sin(q/mod*Pi); if(i<=n-2) { ansx+=x*(n-i)*(n-i-1)/2; ansy+=y*(n-i)*(n-i-1)/2; } if(2<=i&&i<=n-1) { ansx+=x*(i-1)*(n-i); ansy+=y*(i-1)*(n-i); } if(3<=i) { ansx+=x*(i-1)*(i-2)/2; ansy+=y*(i-1)*(i-2)/2; } } ansx*=(3.0/n/(n-1)/(n-2)); ansy*=(3.0/n/(n-1)/(n-2)); printf("%.12lf %.12lf",ansx,ansy); fclose(stdin); fclose(stdout); return 0; }
\(T2\) T2919. 小 w 的代数 \(10pts\)
-
部分分
- 子任务 \(3\) :对于整条链上的每个节点都有选/不选两种选择,且最终得到的非空点集一定合法,故 \(2^{n}-1\) 即为所求,时间复杂度为 \(O(\log n)\) 。
-
正解
- 等学了圆方树再来补。

\(T3\) T2920. 小 y 的数论 \(15pts\)
-
因为本身就是棵树,所以最小斯坦纳树 \(f(S)\) 等价于点集 \(S\) 的虚树。
-
部分分
-
子任务 \(1\) :爆搜后虚树正常做即可,时间复杂度为 \(O(2^{n}qk( \log k+ \log n))\) 。
点击查看代码
struct node { ll nxt,to,w; }e[600010]; ll head[600010],fa[600010],siz[600010],dep[600010],son[600010],top[600010],dis[600010],dfn[600010],pos[600010],tot=0,cnt=0,ans; vector<ll>s,tmp; void add(ll u,ll v,ll w) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; e[cnt].w=w; head[u]=cnt; } void dfs1(ll x,ll father) { tot++; dfn[x]=tot; pos[tot]=x; siz[x]=1; fa[x]=father; dep[x]=dep[father]+1; for(ll i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=father) { dis[e[i].to]=dis[x]+e[i].w; dfs1(e[i].to,x); siz[x]+=siz[e[i].to]; son[x]=(siz[e[i].to]>siz[son[x]])?e[i].to:son[x]; } } } void dfs2(ll x,ll id) { top[x]=id; if(son[x]!=0) { dfs2(son[x],id); for(ll i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=fa[x]&&e[i].to!=son[x]) { dfs2(e[i].to,e[i].to); } } } } ll lca(ll u,ll v) { while(top[u]!=top[v]) { if(dep[top[u]]>dep[top[v]]) { u=fa[top[u]]; } else { v=fa[top[v]]; } } return (dep[u]>dep[v])?v:u; } ll get_dis(ll x,ll y) { x=pos[x]; y=pos[y]; return dis[x]+dis[y]-2*dis[lca(x,y)]; } void dfs(ll pos,ll n,ll k) { if(s.size()==k) { tmp.clear(); for(ll i=0;i<s.size();i++) { tmp.push_back(s[i]); } sort(tmp.begin(),tmp.end()); ll sum=get_dis(tmp[0],tmp.back()); for(ll i=1;i<tmp.size();i++) { sum+=get_dis(tmp[i],tmp[i-1]); } ans=max(ans,sum/2); return; } if(pos==n+1) { return; } else { s.push_back(dfn[pos]); dfs(pos+1,n,k); s.pop_back(); dfs(pos+1,n,k); } } int main() { freopen("number.in","r",stdin); freopen("number.out","w",stdout); ll n,q,u,v,w,l,r,len,k,i; scanf("%lld",&n); for(i=1;i<=n-1;i++) { scanf("%lld%lld%lld",&u,&v,&w); add(u,v,w); add(v,u,w); } dfs1(1,0); dfs2(1,1); scanf("%lld",&q); for(i=1;i<=q;i++) { scanf("%lld%lld%lld",&l,&r,&k); ans=0; dfs(l,r,k); printf("%lld\n",ans); } fclose(stdin); fclose(stdout); return 0; }
-
-
正解


\(T4\) T2921. 小j 的组合 \(15pts\)
-
部分分
- 子任务 \(3\) :整条链本身就是一条哈密顿回路,直接输出 \(1 \sim n\) 即可。
-
正解
- 操作实际上是将 \(v\) 复制给 \(v'\) ,本质是从 \(v\) 的某个子节点回溯到 \(v/v'\) 的过程。
- 然后做法就和 [ABC361E] Tree and Hamilton Path 2 一样了,不在直径上回溯即可。
- 具体地,记录重儿子(子树深度最大的儿子),再次遍历时优先遍历轻儿子,那么最后遍历的一定是直径,通过遍历节点数量特判即可(当深度相同时,难以钦定直径端点在的方向的儿子为重儿子)。
点击查看代码
struct node { int nxt,to; }e[10010]; int head[10010],dep[10010],son[10010],maxx[10010],vis[10010],cnt=0,tot=0,rt=0; vector<int>ans; void add(int u,int v) { cnt++; e[cnt].nxt=head[u]; e[cnt].to=v; head[u]=cnt; } void dfs1(int x,int fa) { maxx[x]=dep[x]=dep[fa]+1; son[x]=0; for(int i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=fa) { dfs1(e[i].to,x); son[x]=(maxx[e[i].to]>maxx[son[x]])?e[i].to:son[x]; maxx[x]=max(maxx[x],maxx[e[i].to]); } } } void dfs2(int x,int fa,int n) { tot++; ans.push_back(x); if(son[x]!=0) { for(int i=head[x];i!=0;i=e[i].nxt) { if(e[i].to!=fa&&e[i].to!=son[x]) { dfs2(e[i].to,x,n); ans.push_back(x); } } dfs2(son[x],x,n); if(tot!=n) { ans.push_back(x); } } } int main() { freopen("combo.in","r",stdin); freopen("combo.out","w",stdout); int n,u,v,rt_sum,i; cin>>n; rt_sum=n; for(i=1;i<=n-1;i++) { cin>>u>>v; add(u,v); add(v,u); } dfs1(1,0); for(i=1;i<=n;i++) { rt=(dep[i]>dep[rt])?i:rt; } dfs1(rt,0); dfs2(rt,0,n); cout<<ans.size()-n<<endl; for(i=0;i<ans.size();i++) { if(vis[ans[i]]==0) { vis[ans[i]]=1; } else { cout<<ans[i]<<" "; rt_sum++; ans[i]=rt_sum; } } cout<<endl; for(i=0;i<ans.size();i++) { cout<<ans[i]<<" "; } fclose(stdin); fclose(stdout); return 0; }
总结
- \(T1\) 赛时猜的结论赶紧有点不符合常识,但因为本场难度过于逆天且 \(T1\) 没有大样例就直接交了。
- 在 C/C++ 插件里通过自动补全捣鼓出一些东西。
-
math.h里的一些常用常数,貌似是 GNU 下独有的(存疑)。点击查看代码
/* Some useful constants. */ #if defined __USE_MISC || defined __USE_XOPEN # define M_E 2.7182818284590452354 /* e */ # define M_LOG2E 1.4426950408889634074 /* log_2 e */ # define M_LOG10E 0.43429448190325182765 /* log_10 e */ # define M_LN2 0.69314718055994530942 /* log_e 2 */ # define M_LN10 2.30258509299404568402 /* log_e 10 */ # define M_PI 3.14159265358979323846 /* pi */ # define M_PI_2 1.57079632679489661923 /* pi/2 */ # define M_PI_4 0.78539816339744830962 /* pi/4 */ # define M_1_PI 0.31830988618379067154 /* 1/pi */ # define M_2_PI 0.63661977236758134308 /* 2/pi */ # define M_2_SQRTPI 1.12837916709551257390 /* 2/sqrt(pi) */ # define M_SQRT2 1.41421356237309504880 /* sqrt(2) */ # define M_SQRT1_2 0.70710678118654752440 /* 1/sqrt(2) */ #endif /* The above constants are not adequate for computation using `long double's. Therefore we provide as an extension constants with similar names as a GNU extension. Provide enough digits for the 128-bit IEEE quad. */ #ifdef __USE_GNU # define M_El 2.718281828459045235360287471352662498L /* e */ # define M_LOG2El 1.442695040888963407359924681001892137L /* log_2 e */ # define M_LOG10El 0.434294481903251827651128918916605082L /* log_10 e */ # define M_LN2l 0.693147180559945309417232121458176568L /* log_e 2 */ # define M_LN10l 2.302585092994045684017991454684364208L /* log_e 10 */ # define M_PIl 3.141592653589793238462643383279502884L /* pi */ # define M_PI_2l 1.570796326794896619231321691639751442L /* pi/2 */ # define M_PI_4l 0.785398163397448309615660845819875721L /* pi/4 */ # define M_1_PIl 0.318309886183790671537767526745028724L /* 1/pi */ # define M_2_PIl 0.636619772367581343075535053490057448L /* 2/pi */ # define M_2_SQRTPIl 1.128379167095512573896158903121545172L /* 2/sqrt(pi) */ # define M_SQRT2l 1.414213562373095048801688724209698079L /* sqrt(2) */ # define M_SQRT1_2l 0.707106781186547524400844362104849039L /* 1/sqrt(2) */ #endif #if __HAVE_FLOAT16 && defined __USE_GNU # define M_Ef16 __f16 (2.718281828459045235360287471352662498) /* e */ # define M_LOG2Ef16 __f16 (1.442695040888963407359924681001892137) /* log_2 e */ # define M_LOG10Ef16 __f16 (0.434294481903251827651128918916605082) /* log_10 e */ # define M_LN2f16 __f16 (0.693147180559945309417232121458176568) /* log_e 2 */ # define M_LN10f16 __f16 (2.302585092994045684017991454684364208) /* log_e 10 */ # define M_PIf16 __f16 (3.141592653589793238462643383279502884) /* pi */ # define M_PI_2f16 __f16 (1.570796326794896619231321691639751442) /* pi/2 */ # define M_PI_4f16 __f16 (0.785398163397448309615660845819875721) /* pi/4 */ # define M_1_PIf16 __f16 (0.318309886183790671537767526745028724) /* 1/pi */ # define M_2_PIf16 __f16 (0.636619772367581343075535053490057448) /* 2/pi */ # define M_2_SQRTPIf16 __f16 (1.128379167095512573896158903121545172) /* 2/sqrt(pi) */ # define M_SQRT2f16 __f16 (1.414213562373095048801688724209698079) /* sqrt(2) */ # define M_SQRT1_2f16 __f16 (0.707106781186547524400844362104849039) /* 1/sqrt(2) */ #endif #if __HAVE_FLOAT32 && defined __USE_GNU # define M_Ef32 __f32 (2.718281828459045235360287471352662498) /* e */ # define M_LOG2Ef32 __f32 (1.442695040888963407359924681001892137) /* log_2 e */ # define M_LOG10Ef32 __f32 (0.434294481903251827651128918916605082) /* log_10 e */ # define M_LN2f32 __f32 (0.693147180559945309417232121458176568) /* log_e 2 */ # define M_LN10f32 __f32 (2.302585092994045684017991454684364208) /* log_e 10 */ # define M_PIf32 __f32 (3.141592653589793238462643383279502884) /* pi */ # define M_PI_2f32 __f32 (1.570796326794896619231321691639751442) /* pi/2 */ # define M_PI_4f32 __f32 (0.785398163397448309615660845819875721) /* pi/4 */ # define M_1_PIf32 __f32 (0.318309886183790671537767526745028724) /* 1/pi */ # define M_2_PIf32 __f32 (0.636619772367581343075535053490057448) /* 2/pi */ # define M_2_SQRTPIf32 __f32 (1.128379167095512573896158903121545172) /* 2/sqrt(pi) */ # define M_SQRT2f32 __f32 (1.414213562373095048801688724209698079) /* sqrt(2) */ # define M_SQRT1_2f32 __f32 (0.707106781186547524400844362104849039) /* 1/sqrt(2) */ #endif #if __HAVE_FLOAT64 && defined __USE_GNU # define M_Ef64 __f64 (2.718281828459045235360287471352662498) /* e */ # define M_LOG2Ef64 __f64 (1.442695040888963407359924681001892137) /* log_2 e */ # define M_LOG10Ef64 __f64 (0.434294481903251827651128918916605082) /* log_10 e */ # define M_LN2f64 __f64 (0.693147180559945309417232121458176568) /* log_e 2 */ # define M_LN10f64 __f64 (2.302585092994045684017991454684364208) /* log_e 10 */ # define M_PIf64 __f64 (3.141592653589793238462643383279502884) /* pi */ # define M_PI_2f64 __f64 (1.570796326794896619231321691639751442) /* pi/2 */ # define M_PI_4f64 __f64 (0.785398163397448309615660845819875721) /* pi/4 */ # define M_1_PIf64 __f64 (0.318309886183790671537767526745028724) /* 1/pi */ # define M_2_PIf64 __f64 (0.636619772367581343075535053490057448) /* 2/pi */ # define M_2_SQRTPIf64 __f64 (1.128379167095512573896158903121545172) /* 2/sqrt(pi) */ # define M_SQRT2f64 __f64 (1.414213562373095048801688724209698079) /* sqrt(2) */ # define M_SQRT1_2f64 __f64 (0.707106781186547524400844362104849039) /* 1/sqrt(2) */ #endif #if __HAVE_FLOAT128 && defined __USE_GNU # define M_Ef128 __f128 (2.718281828459045235360287471352662498) /* e */ # define M_LOG2Ef128 __f128 (1.442695040888963407359924681001892137) /* log_2 e */ # define M_LOG10Ef128 __f128 (0.434294481903251827651128918916605082) /* log_10 e */ # define M_LN2f128 __f128 (0.693147180559945309417232121458176568) /* log_e 2 */ # define M_LN10f128 __f128 (2.302585092994045684017991454684364208) /* log_e 10 */ # define M_PIf128 __f128 (3.141592653589793238462643383279502884) /* pi */ # define M_PI_2f128 __f128 (1.570796326794896619231321691639751442) /* pi/2 */ # define M_PI_4f128 __f128 (0.785398163397448309615660845819875721) /* pi/4 */ # define M_1_PIf128 __f128 (0.318309886183790671537767526745028724) /* 1/pi */ # define M_2_PIf128 __f128 (0.636619772367581343075535053490057448) /* 2/pi */ # define M_2_SQRTPIf128 __f128 (1.128379167095512573896158903121545172) /* 2/sqrt(pi) */ # define M_SQRT2f128 __f128 (1.414213562373095048801688724209698079) /* sqrt(2) */ # define M_SQRT1_2f128 __f128 (0.707106781186547524400844362104849039) /* 1/sqrt(2) */ #endif #if __HAVE_FLOAT32X && defined __USE_GNU # define M_Ef32x __f32x (2.718281828459045235360287471352662498) /* e */ # define M_LOG2Ef32x __f32x (1.442695040888963407359924681001892137) /* log_2 e */ # define M_LOG10Ef32x __f32x (0.434294481903251827651128918916605082) /* log_10 e */ # define M_LN2f32x __f32x (0.693147180559945309417232121458176568) /* log_e 2 */ # define M_LN10f32x __f32x (2.302585092994045684017991454684364208) /* log_e 10 */ # define M_PIf32x __f32x (3.141592653589793238462643383279502884) /* pi */ # define M_PI_2f32x __f32x (1.570796326794896619231321691639751442) /* pi/2 */ # define M_PI_4f32x __f32x (0.785398163397448309615660845819875721) /* pi/4 */ # define M_1_PIf32x __f32x (0.318309886183790671537767526745028724) /* 1/pi */ # define M_2_PIf32x __f32x (0.636619772367581343075535053490057448) /* 2/pi */ # define M_2_SQRTPIf32x __f32x (1.128379167095512573896158903121545172) /* 2/sqrt(pi) */ # define M_SQRT2f32x __f32x (1.414213562373095048801688724209698079) /* sqrt(2) */ # define M_SQRT1_2f32x __f32x (0.707106781186547524400844362104849039) /* 1/sqrt(2) */ #endif #if __HAVE_FLOAT64X && defined __USE_GNU # define M_Ef64x __f64x (2.718281828459045235360287471352662498) /* e */ # define M_LOG2Ef64x __f64x (1.442695040888963407359924681001892137) /* log_2 e */ # define M_LOG10Ef64x __f64x (0.434294481903251827651128918916605082) /* log_10 e */ # define M_LN2f64x __f64x (0.693147180559945309417232121458176568) /* log_e 2 */ # define M_LN10f64x __f64x (2.302585092994045684017991454684364208) /* log_e 10 */ # define M_PIf64x __f64x (3.141592653589793238462643383279502884) /* pi */ # define M_PI_2f64x __f64x (1.570796326794896619231321691639751442) /* pi/2 */ # define M_PI_4f64x __f64x (0.785398163397448309615660845819875721) /* pi/4 */ # define M_1_PIf64x __f64x (0.318309886183790671537767526745028724) /* 1/pi */ # define M_2_PIf64x __f64x (0.636619772367581343075535053490057448) /* 2/pi */ # define M_2_SQRTPIf64x __f64x (1.128379167095512573896158903121545172) /* 2/sqrt(pi) */ # define M_SQRT2f64x __f64x (1.414213562373095048801688724209698079) /* sqrt(2) */ # define M_SQRT1_2f64x __f64x (0.707106781186547524400844362104849039) /* 1/sqrt(2) */ #endif -
一些常用的三角函数(弧度制)
double cos(double x)- 计算并返回 \(x\) 的余弦值(邻边比斜边) \(\cos\) 。
double sin(double x)- 计算并返回 \(x\) 的正弦值(对边比斜边) \(\sin\) 。
double tan(double x)- 计算并返回 \(x\) 的正切值(对边比邻边) \(\tan\) 。
double acos(double x)- 计算并返回范围在 \(0 \sim \pi\) 弧度之间的 \(x\) 的反余弦值。
double asin(double x)- 计算并返回范围在 \(-\frac{\pi}{2} \sim \frac{\pi}{2}\) 弧度之间的 \(x\) 的反余弦值。
double atan(double x)- 计算并返回范围在 \(x\) 的反正切值。
double atan2(double x,double y)- 计算并返回范围在 \(\frac{y}{x}\) 的反正切值。
-
调用 \(\pi\) 的另一个方法是
const double Pi=acos(-1);。
-
- 在 C/C++ 插件里通过自动补全捣鼓出一些东西。
- \(T2\)
- 读假题了,理解错了枚举顺序和编号顺序的关系,导致子任务 \(4,5\) 菊花加树的做法写假了。
- 赛时不会无向图的基环树找环,导致子任务 \(6\) 的 \(15pts\) 的部分分没写,虽然写了也会像子任务 \(4,5\) 一样假掉。
- 题面中对仙人掌的描述太过抽象,换个定义。
- 如果一个无向连通图的每条边最多在一个环里,则称它是一棵 仙人掌 。多棵仙人掌可以组成 沙漠 。
- 仙人掌 满足任意两点间最多有两条边不相交的路径,此性质和定义是等价的。
- \(T2,T4\) 的子任务 \(4\) 把 \(i\) 看出 \(1\) 了,导致菊花的部分分写成了链的部分分。
后记
-
题目来自 accoders NOI 2022NOIP A层联测11 。
-
\(T2,T3,T4\) 的题面有点抽象,理解起来需要花不少时间。
-
温馨提示

本文来自博客园,作者:hzoi_Shadow,原文链接:https://www.cnblogs.com/The-Shadow-Dragon/p/18474785,未经允许严禁转载。
版权声明:本作品采用 「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC BY-NC-SA 4.0) 进行许可。

