暑假集训CSP提高模拟22

暑假集训CSP提高模拟22

\(T1\) P264. 法阵 \(30pts\)

  • 原题： CF1503E 2-Coloring

  • 部分分

    • \(30pts\) ：爆搜。

      点击查看代码 
      const ll p=998244353;
int n,m,c[2010][2010],hang[2010],lie[2010],ans=0;
bool check()
{
	for(int i=1;i<=m;i++)
	{
		if(lie[i]==0)
		{
			return false;
		}
	}
	return true;
}
void dfs(int x,int y)
{
	if(x==n&&y==m)
	{
		if(hang[x]!=0&&check()==true)
		{
			ans=(ans+1)%p;
		}
	}
	else
	{
		if(y==m)
		{
			if(hang[x]!=0)
			{
				dfs(x+1,0);
			}
		}
		else
		{
			if(hang[x]==0)
			{
				if(lie[y+1]==0||c[x-1][y+1]==0)
				{
					c[x][y+1]=0;
					lie[y+1]++;
					dfs(x,y+1);
					lie[y+1]--;
				}
				c[x][y+1]=1;
				hang[x]++;
				dfs(x,y+1);
				c[x][y+1]=0;
				hang[x]--;
			}
			else
			{
				if(c[x][y]==1)
				{
					c[x][y+1]=1;
					hang[x]++;
					dfs(x,y+1);
					hang[x]--;
				}
				if(lie[y+1]==0||c[x-1][y+1]==0)
				{
					c[x][y+1]=0;
					lie[y+1]++;
					dfs(x,y+1);
					lie[y+1]--;
				}
			}
		}
	}
}
int main()
{
	freopen("magic.in","r",stdin);
	freopen("magic.out","w",stdout);
	cin>>n>>m;
	c[1][1]=1;
	hang[1]++;
	dfs(1,1);
	memset(hang,0,sizeof(hang));
	memset(lie,0,sizeof(lie));
	c[1][1]=0;
	lie[1]++;
	dfs(1,1);
	cout<<ans<<endl;
	fclose(stdin);
	fclose(stdout);
	return 0;
}

  • 正解

    • 建议去看 luogu 第一篇题解 。

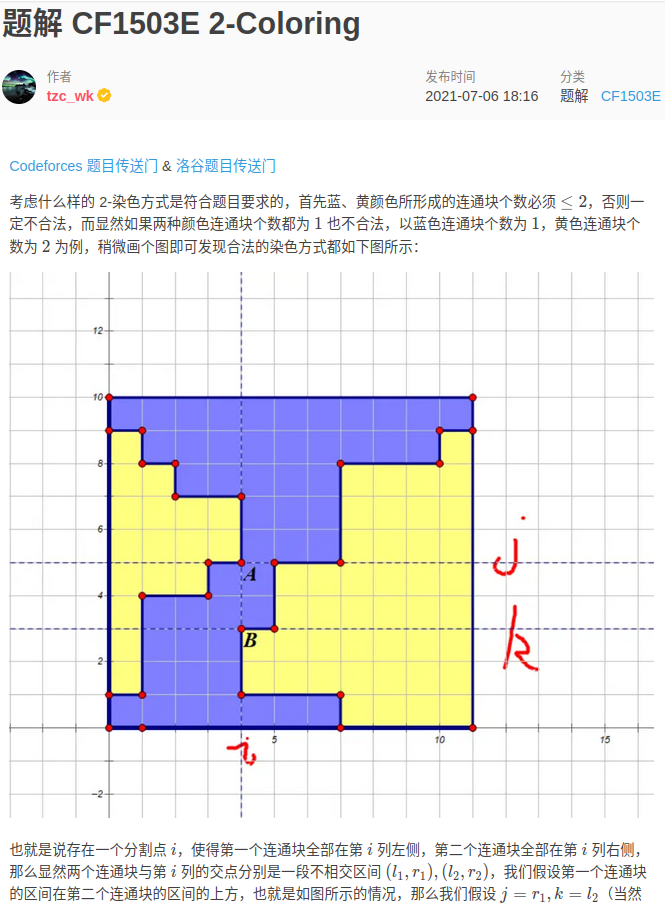
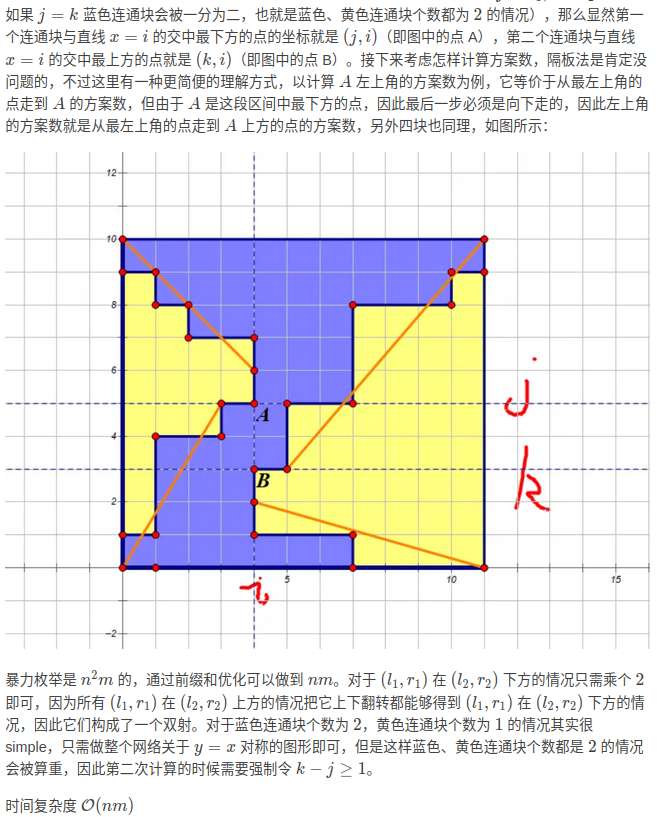
    • 枚举终点 \((i-1,j),(i,j+1),(i,k-1),(i+1,k)\) ，其中 \(k \ge j\) ，分别计算起点 \((0,0),(0,n),(m,0),(n,m)\) 到其的方案数，上下部分乘起来。前缀和优化一部分，枚举另一部分。

    • 接着交换 \(n,m\) ，同上继续计算。但 \(k=j\) 的会算重，令 \(k>j\) 进行更新。

    • 最后乘以 \(2\) 即可。

    点击查看代码 
    const ll p=998244353;
ll inv[5010],jc[5010],jc_inv[5010];
ll C(ll n,ll m,ll p)
{
	return (n>=m&&n>=0&&m>=0)?(jc[n]*jc_inv[n-m]%p)*jc_inv[m]%p:0;
}
ll way(ll x,ll y)
{
	return C(x+y,x,p);
}
int main()
{
	freopen("magic.in","r",stdin);
	freopen("magic.out","w",stdout);
	ll n,m,ans=0,sum=0,i,j;
	cin>>n>>m;
	inv[1]=1;
	jc[0]=jc_inv[0]=jc[1]=jc_inv[1]=1;
	for(i=2;i<=n+m;i++)
	{
		inv[i]=(p-p/i)*inv[p%i]%p;
		jc[i]=jc[i-1]*i%p;
		jc_inv[i]=jc_inv[i-1]*inv[i]%p;
	}
	for(i=1;i<=m-1;i++)
	{
		sum=0;
		for(j=1;j<=n-1;j++)
		{
			sum=(sum+way(i,j-1)*way(i-1,n-j)%p)%p;
			ans=(ans+(sum*way(m-i-1,j)%p)*way(m-i,n-j-1)%p)%p;
		}
	}
	swap(n,m);
	for(i=1;i<=m-1;i++)
	{
		sum=0;
		for(j=1;j<=n-1;j++)
		{
			ans=(ans+(sum*way(m-i-1,j)%p)*way(m-i,n-j-1)%p)%p;
			sum=(sum+way(i,j-1)*way(i-1,n-j)%p)%p;
		}
	}
	cout<<2*ans%p<<endl;
	fclose(stdin);
	fclose(stdout);
	return 0;
}

\(T2\) P265. 连通块 \(66pts\)

  • 原题： luogu P4271 [USACO18FEB] New Barns P | luogu P10238 [yLCPC2024] F. PANDORA PARADOXXX

  • 部分分

    • \(66pts\) ：询问时遍历整棵树。

      点击查看代码 
      struct node
{
	int nxt,to,id;
}e[400010];
int head[200010],vis[200010],cnt=0,ans=0;
void add(int u,int v,int id)
{
	cnt++;
	e[cnt].nxt=head[u];
	e[cnt].to=v;
	e[cnt].id=id;
	head[u]=cnt;
}
void dfs(int x,int fa,int dep)
{
	ans=max(ans,dep);
	for(int i=head[x];i!=0;i=e[i].nxt)
	{
		if(e[i].to!=fa&&vis[e[i].id]==0)
		{
			dfs(e[i].to,x,dep+1);
		}
	}
}
int main()
{
	freopen("block.in","r",stdin);
	freopen("block.out","w",stdout);
	int n,m,u,v,opt,x,i;
	cin>>n>>m;
	for(i=1;i<=n-1;i++)
	{
		cin>>u>>v;
		add(u,v,i);
		add(v,u,i);
	}
	for(i=1;i<=m;i++)
	{
		cin>>opt>>x;
		if(opt==1)
		{
			vis[x]=1;
		}
		else
		{
			ans=0;
			dfs(x,0,0);
			cout<<ans<<endl;
		}
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}

  • 正解

    • 考虑将操作离线下来，然后进行倒序加边。
    • 考虑温习 暑假集训CSP提高模拟4 T4 P136. Black and White 关于点集直径的结论。
      • 设点集 \(A\) 的直径的两个端点为 \(u_{1},v_{1}\) ，另一个点集 \(B\) 的直径的两个端点为 \(u_{2},v_{2}\) ，则 \(A \bigcup B\) 的直径端点一定是 \(\{ u_{1},v_{1},u_{2},v_{2} \}\) 中的两个。
    • 还有另外一个关于直径的结论。
      • 点集 \(A\) 中一个点 \(x\) 到点集中其他点中最远点的距离一定是到直径两个端点的距离取 \(\max\) 。
        • 证明
          • 当 \(x\) 在直径上时，显然。
          • 当 \(x\) 不在直径上时，先走到直径上，就转化到了上述情况。
    • 并查集维护连通块的两个端点即可。
    点击查看代码 
    ll siz[200010],fa[200010],dep[200010],son[200010],top[200010],u[200010],v[200010],opt[200010],x[200010],vis[200010],ans[200010],tot=0,sum=0;
vector<ll>e[200010];
void add(ll u,ll v)
{
	e[u].push_back(v);
}
void dfs1(ll x,ll father)
{
	siz[x]=1;
	fa[x]=father;
	dep[x]=dep[father]+1;
	for(ll i=0;i<e[x].size();i++)
	{
		if(e[x][i]!=father)
		{
			dfs1(e[x][i],x);
			siz[x]+=siz[e[x][i]];
			son[x]=(siz[e[x][i]]>siz[son[x]])?e[x][i]:son[x];
		}
	}
}
void dfs2(ll x,ll id)
{
	top[x]=id;
	if(son[x]!=0)
	{
		dfs2(son[x],id);
		for(ll i=0;i<e[x].size();i++)
		{
			if(e[x][i]!=son[x]&&e[x][i]!=fa[x])
			{
				dfs2(e[x][i],e[x][i]);
			}
		}
	}
}
ll lca(ll u,ll v)
{
	while(top[u]!=top[v])	
	{
		if(dep[top[u]]>dep[top[v]])
		{
			u=fa[top[u]];
		}
		else
		{
			v=fa[top[v]];
		}
	}
	return (dep[u]<dep[v])?u:v;
}
ll ask_dis(ll x,ll y)
{
	return dep[x]+dep[y]-2*dep[lca(x,y)];
}
struct DSU
{
	ll fa[200010],pt[200010][2],tmp[5];
	void init(ll n)
	{
		for(ll i=1;i<=n;i++)
		{
			fa[i]=i;
			pt[i][0]=pt[i][1]=i;
		}
	}
	ll find(ll x)
	{
		return fa[x]==x?x:fa[x]=find(fa[x]);
	}
	void merge(ll x,ll y)
	{
		if(dep[x]>dep[y])
		{
			swap(x,y);
		}
		x=find(x);
		y=find(y);
		fa[y]=x;
		ll maxx=0;
		tmp[1]=pt[x][0];
		tmp[2]=pt[x][1];
		tmp[3]=pt[y][0];
		tmp[4]=pt[y][1];
		for(ll i=1;i<=4;i++)
		{
			for(ll j=i+1;j<=4;j++)
			{
				if(ask_dis(tmp[i],tmp[j])>maxx)
				{
					maxx=ask_dis(tmp[i],tmp[j]);
					pt[x][0]=tmp[i];
					pt[x][1]=tmp[j];
				}
			}
		}
	}
	ll ask(ll x)
	{
		ll y=find(x);
		return max(ask_dis(x,pt[y][0]),ask_dis(x,pt[y][1]));
	}
}D;
int main()
{	
	freopen("block.in","r",stdin);
	freopen("block.out","w",stdout);
	ll n,q,i;
	scanf("%lld%lld",&n,&q);
	D.init(n);
	for(i=1;i<=n-1;i++)
	{
		scanf("%lld%lld",&u[i],&v[i]);
		add(u[i],v[i]);
		add(v[i],u[i]);
	}
	dfs1(1,0);
	dfs2(1,1);
	for(i=1;i<=q;i++)
	{
		scanf("%lld%lld",&opt[i],&x[i]);
		if(opt[i]==1)
		{
			vis[x[i]]=1;
		}
	}
	for(i=1;i<=n-1;i++)
	{
		if(vis[i]==0)
		{	
			D.merge(u[i],v[i]);
		}
	}
	for(i=q;i>=1;i--)
	{
		if(opt[i]==1)
		{
			D.merge(u[x[i]],v[x[i]]);	
		}
		else
		{
			ans[i]=D.ask(x[i]);
		}
	}
	for(i=1;i<=q;i++)
	{
		if(opt[i]==2)
		{
			printf("%lld\n",ans[i]);
		}
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}

\(T3\) P266. 军队 \(20pts\)

  • 部分分

    • \(20pts\) ：\(O(cnm)\) 预处理雄、雌性后 \(O(n \log n)\) 回答单组询问。

      点击查看代码 
      ll val[3010];
int sum[3010][3010],ji[3010],ou[3010];
void add(int x1,int y1,int x2,int y2)
{
	for(int i=x1;i<=x2;i++)
	{
		for(int j=y1;j<=y2;j++)
		{
			sum[i][j]++;
		}
	}
}
ll ask(int x,int y,int n)
{
	ll ans=0;
	for(int i=1;i<=n;i++)
	{
		val[i]=min(ji[i],y/2)*(y-min(ji[i],y/2));
	}
	sort(val+1,val+1+n);
	for(int i=n-x+1;i<=n;i++)
	{
		ans+=val[i];
	}
	return ans;
}
int main()
{
	freopen("army.in","r",stdin);
	freopen("army.out","w",stdout);
	int n,m,c,k,q,x1,y1,x2,y2,x,y,i,j;
	cin>>n>>m>>c>>k>>q;
	for(i=1;i<=c;i++)
	{
		cin>>x1>>y1>>x2>>y2;
		add(x1,y1,x2,y2);
	}
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=m;j++)
		{
			if(sum[i][j]>=k)
			{
				ou[i]++;
			}
			else
			{
				ji[i]++;
			}
		}
		if(ou[i]<ji[i])
		{
			swap(ou[i],ji[i]);
		}
	}
	for(i=1;i<=q;i++)
	{
		cin>>x>>y;
		cout<<ask(x,y,n)<<endl;
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}
  • 正解

    • 不难想到，必须一次性求出一整行内雄、雌性的数量。而这需要用到矩形加，矩形查询考虑扫描线。

    • 观察到 \(k\) 很小，线段树上可以维护每个区间前 \(k\) 种小的数值和它们的出现次数， pushup 时类似归并排序时维护即可。加法的懒惰标记可以使用标记永久化也可以暴力下传。

    • 设每行有 \(a_{i}\) 个雄性，记 \(b_{i}=\min(a_{i},m-a_{i})\) ，从这一行中选 \(y\) 个在 \(\min(b_{i},\left\lfloor \frac{y}{2} \right\rfloor) \times (y-\min(b_{i},\left\lfloor \frac{y}{2} \right\rfloor))\) 时取到最优解。而 \(b_{i}\) 越大原式越容易取到最优解。

    • 将括号拆开，有 \(\min(b_{i},\left\lfloor \frac{y}{2} \right\rfloor) \times y-\min^{2}(b_{i},\left\lfloor \frac{y}{2} \right\rfloor)\) 。

    • 预先处理出 \(\{ b \}\) 及 \(\{ b^{2} \}\) 的前缀和，方便查询。

    • 查询时二分或离线下来双指针处理，前者比后者多带一个 \(\log\) 。

      点击查看代码 
      struct node
{
	int l,r,val;
};
ll a[300010],b[300010],sum1[300010],sum2[300010];
vector<node>e[300010];
struct SMT
{
	struct SegmentTree
	{
		int l,r,lazy;
		vector<pair<int,int> >num;
	}tree[1200010];
	int lson(int x)
	{
		return x*2;
	}
	int rson(int x)
	{
		return x*2+1;
	}
	void pushup(int rt,int k)
	{
		tree[rt].num.clear();
		int x=0,y=0;
		while(x<tree[lson(rt)].num.size()&&y<tree[rson(rt)].num.size())
		{
			if(tree[lson(rt)].num[x].first<tree[rson(rt)].num[y].first)
			{
				tree[rt].num.push_back(tree[lson(rt)].num[x]);
				x++;
			}
			else
			{	
				if(tree[lson(rt)].num[x].first==tree[rson(rt)].num[y].first)
				{
					tree[rt].num.push_back(make_pair(tree[lson(rt)].num[x].first,tree[lson(rt)].num[x].second+tree[rson(rt)].num[y].second));
					x++;
					y++;
				}
				else
				{
					tree[rt].num.push_back(tree[rson(rt)].num[y]);
					y++;
				}
			}
		}
		while(x<tree[lson(rt)].num.size())
		{
			tree[rt].num.push_back(tree[lson(rt)].num[x]);
			x++;
		}
		while(y<tree[rson(rt)].num.size())
		{
			tree[rt].num.push_back(tree[rson(rt)].num[y]);
			y++;
		}
		while(tree[rt].num.size()>k)
		{
			tree[rt].num.pop_back();
		}
	}
	void build(int rt,int l,int r,int k)
	{
		tree[rt].l=l;
		tree[rt].r=r;
		if(l==r)
		{
			tree[rt].num.push_back(make_pair(0,1));
			return;
		}
		int mid=(l+r)/2;
		build(lson(rt),l,mid,k);
		build(rson(rt),mid+1,r,k);
		pushup(rt,k);
	}
	void pushdown(int rt)
	{
		if(tree[rt].lazy!=0)
		{
			for(int i=0;i<tree[lson(rt)].num.size();i++)
			{
				tree[lson(rt)].num[i].first+=tree[rt].lazy;
			}
			for(int i=0;i<tree[rson(rt)].num.size();i++)
			{
				tree[rson(rt)].num[i].first+=tree[rt].lazy;
			}
			tree[lson(rt)].lazy+=tree[rt].lazy;
			tree[rson(rt)].lazy+=tree[rt].lazy;
			tree[rt].lazy=0;
		}
	}
	void update(int rt,int x,int y,int val,int k)
	{
		if(x<=tree[rt].l&&tree[rt].r<=y)
		{
			for(int i=0;i<tree[rt].num.size();i++)
			{
				tree[rt].num[i].first+=val;
			}
			tree[rt].lazy+=val;
			return;
		}
		pushdown(rt);
		int mid=(tree[rt].l+tree[rt].r)/2;
		if(x<=mid)
		{
			update(lson(rt),x,y,val,k);
		}
		if(y>mid)
		{
			update(rson(rt),x,y,val,k);
		}
		pushup(rt,k);
	}
}T;
int main()
{
	freopen("army.in","r",stdin);
	freopen("army.out","w",stdout);
	int c,k,q,x1,y1,x2,y2,i,j;
	ll n,m,x,y,pos;
	scanf("%lld%lld%d%d%d",&n,&m,&c,&k,&q);
	for(i=1;i<=c;i++)
	{
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		e[x1].push_back((node){y1,y2,1});
		e[x2+1].push_back((node){y1,y2,-1});
	}
	T.build(1,1,m,k);
	for(i=1;i<=n;i++)
	{
		for(j=0;j<e[i].size();j++)
		{
			T.update(1,e[i][j].l,e[i][j].r,e[i][j].val,k);
		}
		for(j=0;j<T.tree[1].num.size();j++)
		{
			if(T.tree[1].num[j].first<k)
			{
				a[i]+=T.tree[1].num[j].second;
			}
			else
			{
				break;
			}
		}
		b[i]=min(a[i],m-a[i]);
	}
	sort(b+1,b+1+n);
	for(i=1;i<=n;i++)
	{
		sum1[i]=sum1[i-1]+b[i];
		sum2[i]=sum2[i-1]+b[i]*b[i];
	}
	for(i=1;i<=q;i++)
	{
		scanf("%lld%lld",&x,&y);
		pos=lower_bound(b+1,b+1+n,y/2)-b;
		if(n-pos+1>=x)
		{
			printf("%lld\n",x*(y/2)*(y-y/2));
		}
		else
		{
			printf("%lld\n",(n-pos+1)*(y/2)*(y-y/2)+y*(sum1[pos-1]-sum1[n-x+1-1])-(sum2[pos-1]-sum2[n-x+1-1]));
		}
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}

\(T4\) P267. 棋盘 \(20pts\)

  • 部分分

    • \(20 \sim 30pts\) ：暴力进行转移，时间复杂度为 \(O(nq^{2})\) 。

      点击查看代码 
      const int p=998244353;
int f[100010][30],dx[5]={0,1,1,2,2},dy[5]={0,-2,2,-1,1};
char s[100010][30],pd[5];
int ask(int up,int down,int x,int y,int n)
{
	if(s[up][x]=='#'||s[down][y]=='#'||up>down)
	{
		return 0;
	}
	memset(f,0,sizeof(f));
	f[up][x]=1;
	for(int i=up;i<=down;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(s[i][j]=='.')
			{
				for(int k=1;k<=4;k++)
				{
					int ni=i+dx[k],nj=j+dy[k];
					if(up<=ni&&ni<=down&&1<=nj&&nj<=n&&s[ni][nj]=='.')
					{
						f[ni][nj]=(f[ni][nj]+f[i][j])%p;
					}
				}
			}
		}
	}
	return f[down][y];
}
int main()
{
	freopen("chess.in","r",stdin);
	freopen("chess.out","w",stdout);
	int n,q,up=1,down=0,x,y,i;
	scanf("%d%d",&n,&q);
	for(i=1;i<=q;i++)
	{
		scanf("%s",pd+1);
		if(pd[1]=='A')
		{
			down++;
			scanf("%s",s[down]+1);
		}
		if(pd[1]=='D')
		{
			up++;
		}
		if(pd[1]=='Q')
		{
			scanf("%d%d",&x,&y);
			printf("%d\n",ask(up,down,x,y,n));
		}
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}
  • 正解

    • 逆天题面，挂下官方题解。

总结

  • \(T2\) 想成了启发式合并，赛后改题时发现思路假了，无法支持 \(lazy\) 标记的下传，挂下赛时思路。
    • 设 \(dis_{x,y}\) 表示 \(x,y\) 间的距离， \(ans_{x}\) 表示 \(x\) 所在的连通块中离 \(x\) 最远的点的距离。
    • 加边时考虑启发式合并，设要将 \(y\) 的父亲设为 \(x\) 。接着顺序进行如下操作从而更新答案：
      • \(dis_{x,z}=dis_{y,z}+1,ans'_{z}=\max(ans_{z},dis_{y,z}+ans_{x}+1) (z \in Subtree(y))\)
      • \(ans'_{z}=\max(ans_{z},dis_{x,z}+ans_{y}+1)(z \in Subtree(x),z \notin Subtree(y))\)
      • \(ans_{z}=ans'_{z}\)
    • \(dis\) 的更新可以直接通过打标记来实现，而 \(\max\) 可以拆成两部分，只选择维护后面增加的 \(ans_{x}+1/ans_{y}+1\) 。
    • 更新时先下传 \(dis\) 的懒惰标记再下传 \(\max\) 的增量标记。

后记

  • 今天早上 \(7:00\) 才开始往题库里搬，教练懒得截 \(PDF\) 挨个挂题面，所以直接下发了 \(PDF\) 文件。题目部分只有如下部分。

  • \(T3\) 抽象的题目背景。

  • 附题解最后被去掉的部分。

posted @ 2024-08-16 18:03  hzoi_Shadow  阅读(78)  评论(2)  编辑  收藏  举报
扩大
缩小