暑假集训CSP提高模拟14

合集 - 2024暑假集训(47)

1.高一上六月下旬日记2024-06-272.【MX-S1】梦熊周赛 · 提高组 1（同步赛）2024-06-293.牛客周赛 Round 492024-07-014.高一上七月上旬日记2024-07-015.Denso Create Programming Contest 2024（AtCoder Beginner Contest 361）2024-07-076.NOIP2024模拟12024-07-087.NOIP2024模拟22024-07-108.高一上七月中旬日记2024-07-119.NOIP2024模拟32024-07-1110.CSP提高组模拟12024-07-1211.暑假集训CSP提高模拟12024-07-1812.暑假集训CSP提高模拟22024-07-1913.暑假集训CSP提高模拟32024-07-2014.暑假集训CSP提高模拟42024-07-2115.高一上七月下旬日记2024-07-2216.暑假集训 加赛12024-07-2217.暑假集训CSP提高模拟52024-07-2318.暑假集训CSP提高模拟62024-07-2419.加赛22024-07-2420.暑假集训CSP提高模拟72024-07-2521.暑假集训CSP提高模拟82024-07-2622.暑假集训CSP提高模拟92024-07-2723.暑假集训CSP提高模拟102024-07-2824.暑假集训CSP提高模拟112024-07-2925.暑假集训CSP提高模拟122024-07-3126.高一上八月上旬日记2024-07-3127.暑假集训CSP提高模拟132024-08-0128.欢欢乐乐赛赛2024-08-02

29.暑假集训CSP提高模拟142024-08-06

30.暑假集训CSP提高模拟152024-08-0731.暑假集训CSP提高模拟162024-08-0832.暑假集训CSP提高模拟172024-08-1033.高一上八月中旬日记2024-08-1134.暑假集训CSP提高模拟182024-08-1135.暑假集训CSP提高模拟192024-08-1236.暑假集训CSP提高模拟202024-08-1437.暑假集训CSP提高模拟212024-08-1538.暑假集训CSP提高模拟222024-08-1639.【LGR-196-Div.4】洛谷入门赛 #262024-08-1940.暑假集训CSP提高模拟232024-08-1741.牛客周赛 Round 562024-08-1942.暑假集训CSP提高模拟242024-08-1943.暑假集训CSP提高模拟 252024-08-2044.高一上八月下旬日记2024-08-2045.暑假集训CSP提高模拟262024-08-2146.暑假集训CSP提高模拟272024-08-2247.牛客小白月赛992024-08-24

收起

暑假集训CSP提高模拟14

组题人： @H_Kaguya | @LYinMX

$T1$ P209.BA $30pts$

• 部分分

  • $30pts$ ：输出 $\lceil {\displaystyle \frac{\sum _{i=1}^m{a}_i}{n}}\rceil$ 。

• 数形结合，将 $\{a\}$ 抽象成矩形，烙饼抽象成海报覆盖，最终有 $max(\underset{i=1}{\overset{m}{max}}\{a_i\},\lceil {\displaystyle \frac{\sum _{i=1}^m{a}_i}{n}}\rceil )$ 即为所求，注意精度（？）。

  点击查看代码

  int main()
  {
  	ll n,m,x,sum=0,maxx=0,i;
  	cin>>m>>n;
  	for(i=1;i<=m;i++)
  	{
  		cin>>x;
  		sum+=x;
  		maxx=max(maxx,x);
  	}
  	cout<<max(maxx,(sum+n-1)/n)<<endl;
  	return 0;
  }
  

$T2$ P210. BB $25pts$

• 原题： luogu P9133 [THUPC 2023 初赛] 大富翁

• 部分分

  • $25pts$ ：枚举所有合法状态， $DFS$ 序加树状数组维护子树内信息，暴力跳父亲，由买方是 $A$ 还是 $B$ 决定取最大值还是最小值转移，因为只能应付 $n$ 很小的数据，所以暴力跳父亲比树剖维护路径信息会快点（？）。、

    • 实测树剖全部 $TLE$ ，实际 $O({\log }^{2}n)$ 的维护路径信息不如暴力跳父亲的 $O(n)$ 。

      点击查看代码

      struct node
      {
      	ll nxt,to;
      }e[400010];
      ll head[400010],w[400010],fa[400010],dfn[400010],out[400010],a[400010],vis[400010],tot=0,cnt=0;
      struct BIT
      {
      	ll c[400010];
      	void init()
      	{
      		memset(c,0,sizeof(c));
      	}
      	ll lowbit(ll x)
      	{
      		return (x&(-x));
      	}
      	void add(ll n,ll x,ll val)
      	{
      		for(ll i=x;i<=n;i+=lowbit(i))
      		{
      			c[i]+=val;
      		}
      	}
      	ll getsum(ll x)
      	{
      		ll ans=0;
      		for(ll i=x;i>=1;i-=lowbit(i))
      		{
      			ans+=c[i];
      		}
      		return ans;
      	}
      	ll ask(ll l,ll r)
      	{
      		return getsum(r)-getsum(l-1);
      	}
      }A,B;
      void add(ll u,ll v)
      {
      	cnt++;
      	e[cnt].nxt=head[u];
      	e[cnt].to=v;
      	head[u]=cnt;
      }
      void dfs(ll x)
      {
      	tot++;
      	dfn[x]=tot;
      	for(ll i=head[x];i!=0;i=e[i].nxt)
      	{
      		dfs(e[i].to);
      	}
      	out[x]=tot;
      }
      ll dp(ll pos,ll n,ll sum)
      {
      	if(pos==n+1)
      	{
      		return sum;
      	}
      	else
      	{
      		ll minn=0x7f7f7f7f,maxx=-0x7f7f7f7f,n1,n2,x;
      		if(pos%2==1)
      		{
      			for(ll i=1;i<=n;i++)
      			{
      				if(vis[i]==0)
      				{
      					n1=n2=0;
      					x=i;
      					while(x!=1)
      					{
      						x=fa[x];
      						n2+=(vis[x]==-1);
      					}
      					n1=B.ask(dfn[i],out[i]);
      					vis[i]=1;
      					A.add(n,dfn[i],1);
      					maxx=max(maxx,dp(pos+1,n,sum+n1-n2-w[i]));
      					A.add(n,dfn[i],-1);
      					vis[i]=0;
      				}
      			}
      			return maxx;
      		}
      		else
      		{
      			for(ll i=1;i<=n;i++)
      			{
      				if(vis[i]==0)
      				{
      					n1=n2=0;
      					x=i;
      					while(x!=1)
      					{
      						x=fa[x];
      						n2+=(vis[x]==1);
      					}
      					n1=A.ask(dfn[i],out[i]);
      					vis[i]=-1;
      					B.add(n,dfn[i],1);
      					minn=min(minn,dp(pos+1,n,sum-(n1-n2)));
      					B.add(n,dfn[i],-1);
      					vis[i]=0;
      				}
      			}
      			return minn;
      		}
      	}
      }
      int main()
      {
      	ll n,i;
      	cin>>n;
      	for(i=1;i<=n;i++)
      	{
      		cin>>w[i];
      	}
      	for(i=2;i<=n;i++)
      	{
      		cin>>fa[i];
      		add(fa[i],i);
      	}
      	dfs(1);
      	cout<<dp(1,n,0)<<endl;
      	return 0;
      }
      

• 正解

  • 买方每次购买一个点都会得到 $n_1-n_2-w_x$ 个游戏币，相应的对方减少 $n_1-n_2$ 个游戏币即得到 $n_2-n_1$ 个游戏币。
  • 当购买一个点后，给祖先每个点的所属对象（不管是现在还是未来）交一个游戏币，这样的话仍满足题意。那么一个点对答案产生的贡献就是 $si{z}_x-1-(de{p}_x-1)-w_x=si{z}_x-de{p}_x-w_x$ 。
    • 实际上就是顺序不会影响最终结果。
  • 排序后跳着选即可。
  点击查看代码

  struct node
  {
  	ll nxt,to;
  }e[400010];
  ll head[400010],w[400010],siz[400010],dep[400010],fa[400010],cnt=0;
  void add(ll u,ll v)
  {
  	cnt++;
  	e[cnt].nxt=head[u];
  	e[cnt].to=v;
  	head[u]=cnt;
  }
  void dfs(ll x)
  {
  	siz[x]=1;
  	dep[x]=dep[fa[x]]+1;
  	for(ll i=head[x];i!=0;i=e[i].nxt)
  	{
  		dfs(e[i].to);
  		siz[x]+=siz[e[i].to];
  	}
  }
  int main()
  {
  	ll n,ans=0,i;
  	cin>>n;
  	for(i=1;i<=n;i++)
  	{
  		cin>>w[i];
  	}
  	for(i=2;i<=n;i++)
  	{
  		cin>>fa[i];
  		add(fa[i],i);
  	}
  	dfs(1);
  	for(i=1;i<=n;i++)
  	{
  		w[i]=siz[i]-dep[i]-w[i];
  	}
  	sort(w+1,w+1+n);
  	for(i=n;i>=1;i-=2)
  	{
  		ans+=w[i];
  	}
  	cout<<ans<<endl;
  	return 0;
  }
  

$T3$ P211. BC $0pts$

• 部分分都不会打，弃了。

  

$T4$ P212. BD $0pts$

• 同上。

  

  

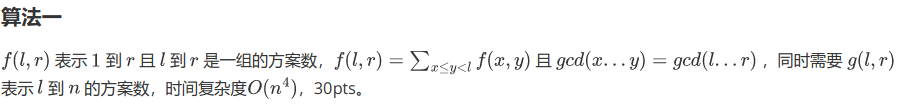
总结

• 赛时历程： $2min$ 写完 $T1$ 后开始写 $T2$ ，没看到最优策略所以写的 next_permutation 发现比答案大且不止一种情况后开始写暴搜，写到 $9:30$ 就过小样例了，尝试用树剖优化却不如暴力。然后就开始罚坐加背《蜀道难》。
• $T1$ 测过大样例后没再造其他数据检验，导致挂了 $70pts$ 。

后记

• 最低暴力分数线： $11pts+0pts+\{0pts,11pts\}+30pts$ ，除 @xrlong 外全员需要背《蜀道难》， @LYinMX 本来想督促我们打部分分的，结果发现都没打部分分，被迫称有想背的可以找任意学长背。

  

• $10:00$ 左右才下发大样例。

• $11:00$ 左右下发了《蜀道难》.zip 。

  

  

  

• $T1$ 输入格式错了，赛时没有更改。

• $T3$ 题面 @LYinMX 少抄了，样例也抄错一个，赛时更改了，发了公告，但没有弹窗提醒导致大部分人都没看到。